基于ABAQUS的汽车驱动桥壳改进设计

桑 楠

(常州工学院,江苏常州 213002)

0 引 言

汽车驱动桥壳是汽车的主要承载件,与从动桥共同支承车架及其上的各总成重量(簧载质量),承受由车轮传来的路面反作用力和力矩。驱动桥壳又是主减速器、差速器及驱动车轮传动装置的外壳。因而驱动桥壳应具有足够强度和刚度,便于主减速器的拆装和调整。驱动桥壳设计时应满足应力和变形要求,避免因局部应力集中导致桥壳的断裂或塑性变形。因此,对驱动桥壳进行应力、变形分析,提高工作可靠性具有非常重要的意义。但汽车驱动桥壳形状复杂,且汽车的行驶条件千变万化,利用传统方法很难精确计算桥壳各处的应力及变形大小。然而,利用有限单元方法对其进行计算和分析可以得到较为准确的分析结果。ABAQUS是一款功能强大的有限元分析软件,可以分析复杂的固体力学、结构力学系统,特别是能够驾驭非常庞大复杂的问题和模拟高度非线性问题。ABAQUS不但可以做单一零件的力学和多物理场的分析,同时,还可以做复杂系统级的分析和研究。因此,被广泛应用于汽车设计领域。文中运用ABAQUS分析结果进行改进设计,所研究的对象是在某型号面包车上使用的组合式桥壳。

1 驱动桥壳强度的理论分析计算

在传统的理论计算中,将驱动桥壳视为一空心横梁,两端经轮毂轴承支撑于车轮上,在钢板弹簧座处桥壳承受汽车的簧载质量,而沿左右轮胎中心线,地面给轮胎以反力,受力如图1所示[1-2]。

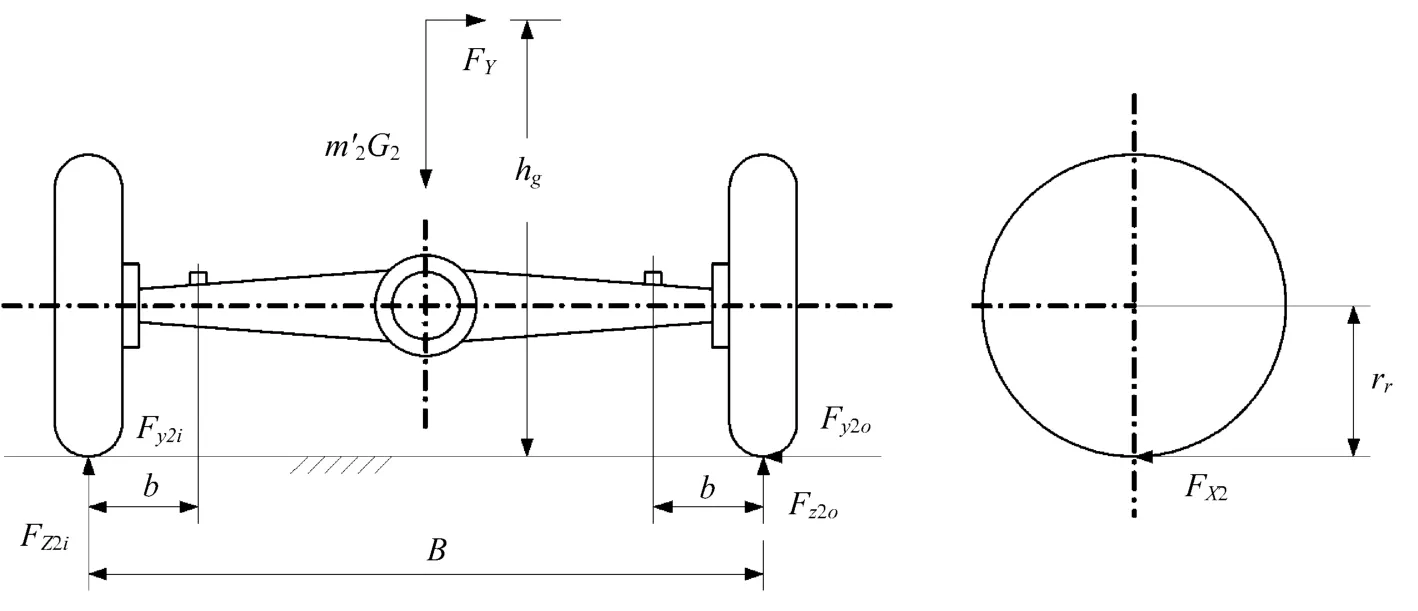
图1 驱动桥壳的受力简图

文献[1-2]把桥壳强度计算简化为3种载荷工况,只要在这3种载荷计算工况下桥壳的强度得到保证,就认为该桥壳在汽车行驶条件下是可靠的。

(1)纵向力FX2最大,侧向力FY2=0,板簧座处弯曲应力σ和扭转切应力τ(危险断面为矩形断面)分别为:

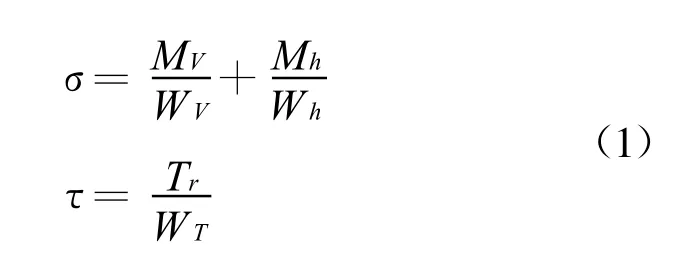
式中:MV垂直力FZ2在垂直平面的弯矩,,其中,b为轮胎中心平面到板簧座之间的横向距离,m2为负荷转移系数,G2为汽车总重在驱动轮上的静负荷;

Mh水平力FX2在水平面内引起的弯矩,Mh=FX2b;

Tr水平力FX2在危险断面所引起的扭矩

WT危险断面抗扭截面系数。危险截面为圆形断面,抗弯截面系数为W,弯扭合成应力σh为:

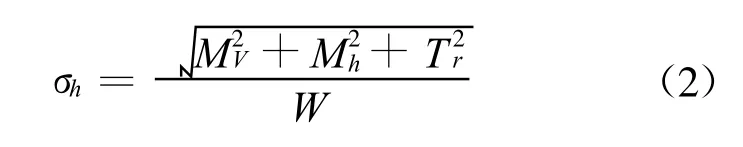
(2)侧向力FY2最大,FX2=0时,桥壳内、外板簧座处断面的弯曲应力σi,σo之间的关系分别为:

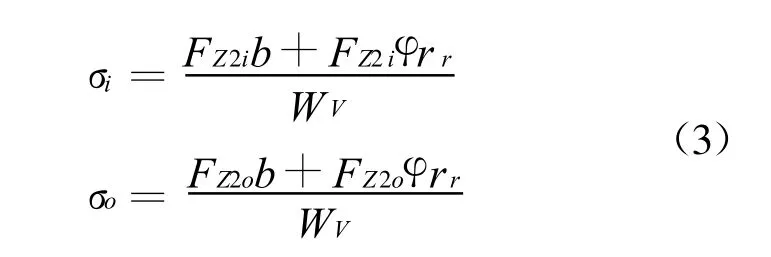
式中:FZ2i,FZ2o分别为内外车轮所受垂直反力;

rr车轮半径。

(3)当汽车通过不平路面时,危险断面的弯曲应力为:

上述传统计算方法对于结构简单、形状规则的构件能够得到较为精确的结果。但对于汽车驱动桥壳来讲,其结构复杂,各断面形状差异较大,采用上述计算方法不能完全反映桥壳各处的应力与应变情况,特别是桥壳应力集中的地方无法反映其真实的应力数值。而在实际使用中,桥壳的破坏通常是从应力集中的地方开始的,为避免此情况发生,设计者往往采用加大零件的尺寸来保证。而使用有限元法对驱动桥壳进行强度分析,只要计算模型简化得当,受力约束处理合理,就可以得到比较详细的应力与变形的分布情况,这些都是上述传统计算方法所难以办到的。

2 桥壳ABAQUS有限元分析模型

文中分析的模型为国内某汽车公司生产的微型面包车。原设计方案在实际使用中桥壳鼓包处出现开裂现象,因此,在改进设计中进行了3种方案的对比分析。方案1:原车状态;方案2:桥壳鼓包处增加加强板;方案3:桥壳鼓包及桥壳圆管均增加壁厚1 mm。

2.1 建立ABAQUS有限元模型

有限元分析结果可信度的高低直接受分析模型、载荷处理、约束条件和实际工程结构力学特性符合程度的影响,建立有限元分析模型时既要如实反映实际结构的重要力学特性,又要尽量采用较少的单元和简单的单元形态,以保证较高的计算精度及缩小解题规模[3]。

驱动桥壳Pro/E三维模型如图2所示。

图2 驱动桥壳Pro/E三维模型

由于汽车零部件结构形状较为复杂,包含许多复杂曲面,而一般有限元软件所提供的几何建模工具功能相当有限,难以快速方便地对其建模。因此,文中采用先用Pro/E建立三维模型(见图2,在进行有限元分析时为减少计算量进行了必要的简化),再导入ABAQUS中的建模方法。在Pro/E中可以方便快捷地建立结构模型,导入ABAQUS时,利用ABAQUS的模型修复功能,消除几何模型中可能存在的如自由边、小平面、小尖角、微小缝隙等几何缺陷。这样采用Pro/E和ABAQUS相结合的建模方法,可以得到较为精确的几何模型。一般来说,桥壳的ABAQUS模型在整个有限元求解过程中,最重要的环节是有限元前处理模型的建立。这一般包括几何建模、定义材料属性和实常数(要根据单元的几何特性来设置,有些单元没有实常数)、定义单元类型,网格划分、添加约束与载荷等。

网格划分质量的好坏直接影响求解精度和求解时间,不合理的网格甚至会导致求解过程的中断,所以网格划分应该是分析过程中需要重点注意的一个环节[4-5]。运用ABAQUS强大而便捷的网格划分功能,通过在模型上设置全局种子的方法合理地控制网格密度。将形状不规则的桥壳几何模型分割成几个形状规则的几何体,运用结构化和扫掠的网格划分方法,这样就可以采用六面体单元得到规则和合理的网格。ABAQUS提供了数量众多的单元种类以满足各种分析类型的需要,文中采用C3D8R单元[6],即实体三维八节点六面体线性缩减积分单元。C3D8R单元的求解结果较精确,而且当网格存在扭曲变形时分析精度不会受到大的影响。

方案1、方案2和方案3的有限元分析模型分别如图3～图5所示。

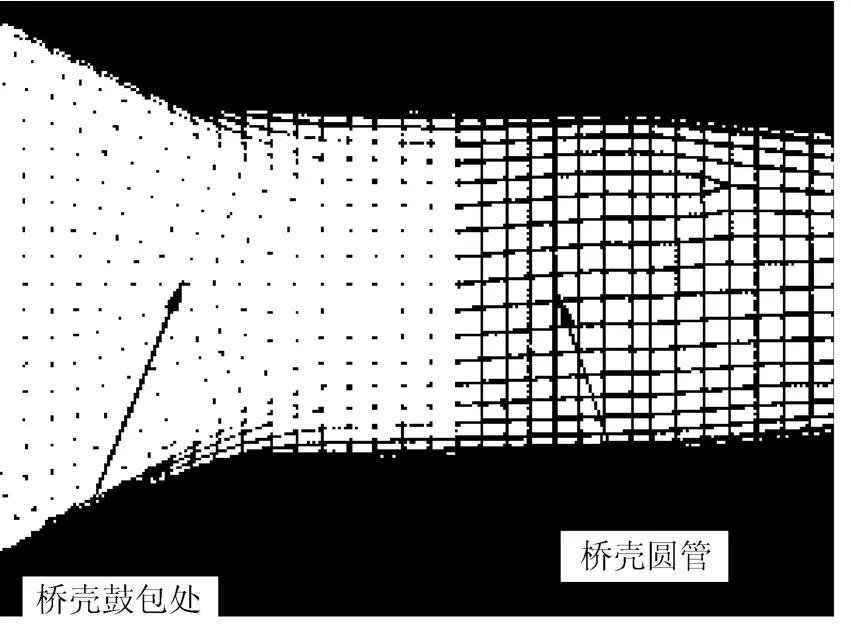
图3 方案1有限元分析模型

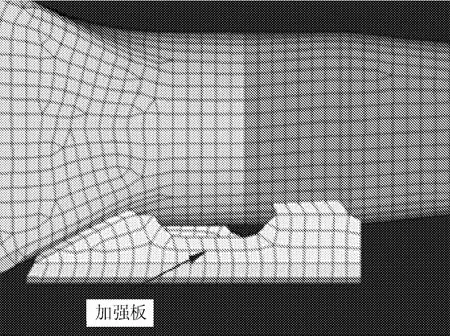
图4 方案2有限元分析模型

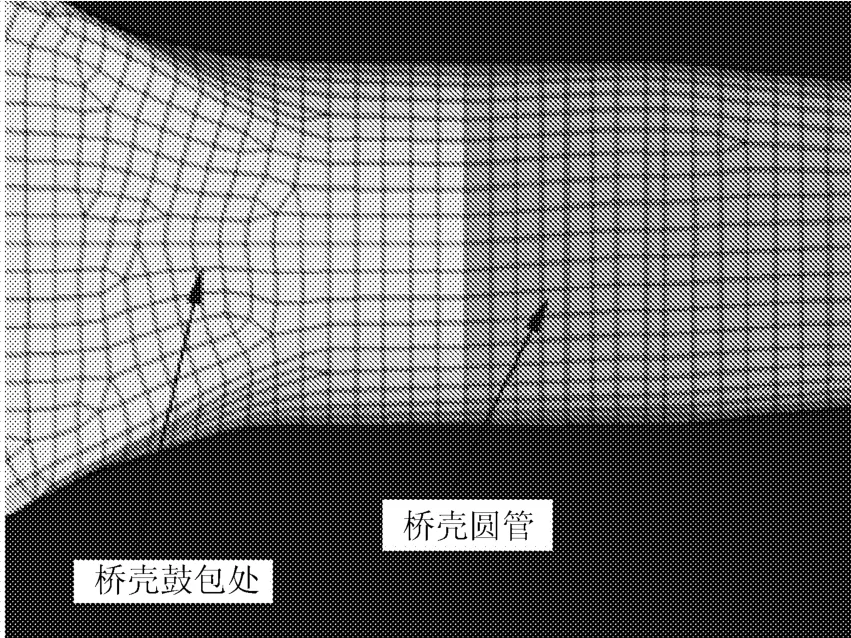
图5 方案3有限元分析模型

2.2 载荷与边界条件

边界约束条件施加是否合理直接影响到分析结果的正确性和合理性。根据国家标准,当承受满载轴荷时,桥壳最大变形量不能超过1.5 mm/m;承受2.5倍满载轴荷时,桥壳不能出现断裂和塑性变形。所以根据计算在板簧处分别加650 kg垂直载荷,两端轴承座中心保持铰接状态。

3 计算结果分析

3.1 应力分析

文中所分析桥壳的材料屈服限为245 MPa,在2.5倍满载轴荷时,桥壳不能出现断裂和塑性变形。其分析结果见表1。

表1 各模型分析结果

方案2和方案3的应力云图分别如图6和图7所示。

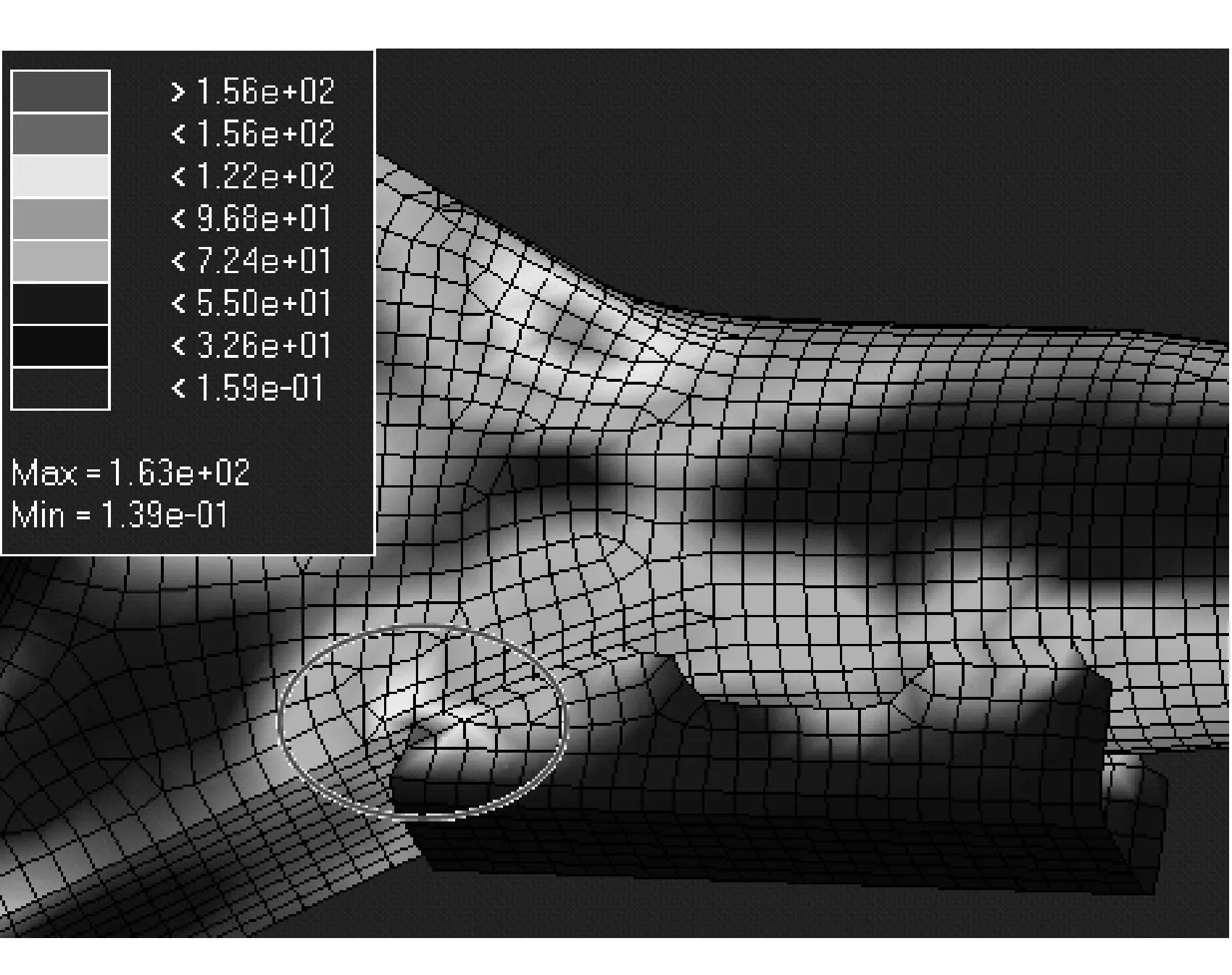
图6 方案2的模型Mises应力云图

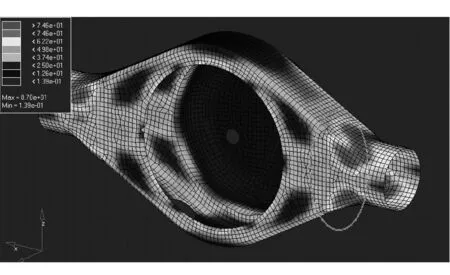
图7 方案3的模型Mises应力云图

方案1在实际使用中出现桥壳开裂现象,从有限元分析的结果看,无论是在桥壳鼓包处还是在桥壳圆管处的应力均超过设计的目标值,最大值出现在桥壳鼓包处为138 MPa。这也表明,用传统的计算方法设计计算复杂结构的零件时,其计算结果往往与实际偏差较大,为保证在实际使用中的可靠性,通常加大零件结构尺寸,增加了零件的重量,同时成本也相应增加[7-8]。

方案2的加强板与桥壳鼓包连接处出现应力集中(图示标记处),应力最大值为163 MPa。表明增加加强板后反而更加引起应力集中,其原因是在连接处截面发生了突变,说明单纯增加加强板不能提高桥壳的强度,反而降低了桥壳的强度,此方案不可用。

方案3在桥壳鼓包处仍然存在应力集中,但最大应力数值明显比其它方案低,也低于目标值。

分析结论:方案1和方案2均应力远远超过目标值;方案2增加加强板反而引起应力更加集中;方案3满足设计目标;各方案应力最大值基本位于对应的同一区域。

3.2 变形分析

根据汽车后桥试验要求,后桥垂直最大变形应小于1.5 mm/m,根据本车型后桥长度计算,设计目标值应小于2.0 mm。方案3的变形图如图8所示。

图8 方案3模型变形图

其它方案变形数据见表2。

表2 各方案模型变形

表中数据表明,方案1的变形大于方案2,加强板只增加了桥壳的刚度,并没有增加其强度,其原因如前所述,是应力集中降低了桥壳的强度。方案3在桥壳鼓包和桥壳圆管处均增加1 mm,强度和刚度均明显增加,且都小于设计的目标值,满足要求。因此,零件的强度不仅仅在于尺寸的大小,其结构的好坏是影响其强度与刚度的非常重要的因素。

4 结 语

(1)在桥壳鼓包处增加加强板,不能增加桥壳的强度,也不能解决桥壳开裂现象;

(2)增加桥壳鼓包处的厚度能显著提高桥壳的强度,可以有效解决桥壳开裂现象,实际使用表明方案3是可行的;

(3)在设计中使用有限元方法,可以缩短设计开发周期,降低设计开发成本,减少试验次数,提高产品质量,使得汽车在轻量化、舒适性和操纵稳定性方面得到改进和提高,具有非常重大的实际意义。

[1] 刘 涛.汽车设计[M].北京:北京大学出版社,2008.

[2] 刘惟信.车桥设计[M].北京:机械工业出版社,2004.

[3] 黄克智.ABQUS/Standard有限元入门指南[M].北京:清华大学出版社,1998.

[4] 庄 茁.基于ABAQ US的有限元分析和应用[M].北京:清华大学出版社,2009.

[5] 石亦平,周玉蓉.ABAQUS有限元分析实例详解[M].北京:机械工业出版社,2006.

[6] 邱智学,黄菊花.ABAQUS壳单元在有限元分析中的应用研究[J].模具技术,2003,5:69-71.

[7] 薛 军,孙宝玉.基于有限元法的齿轮齿条动态应力分析[J].长春工业大学学报:自然科学版,2008,29(3):275-278.

[8] 李 博.基于ABAQUS的液压机工作台优化设计[M].沈阳:沈阳机械设计与制造出版社,2009.