呼叫中心ACD话务分配优化模型探讨

史宝虹

（西安外国语大学，西安 710128）

0 引言

呼叫中心(Call Center )是企业与客户沟通的桥梁，为客户提供信息服务。呼叫中心以计算机电话集成(Computer Telephony Integration CTI) 技术为基础，结合通信网、计算机网产品构建系统硬件平台，将电话咨询与客户主动关怀业务融入系统，兼顾人性化友好服务界面、自动电话查询、快速处理和不间断服务的优点，允许客户通过简单方法获取信息服务[1]。现代呼叫中心核心关键技术以ACD、VOIP和SMS技术为代表，随着计算机网络和语音技术的飞速发展，其应用前景正变得越来越广阔。

自动呼叫分配 (Automatic Call Distribution，ACD)，是现代呼叫中心有别于一般的热线电话和自动应答系统的重要技术[2]。ACD系统可以自动把正在排队等待的呼叫按照一定的规则路由到相应的坐席代表处，把大量的呼叫进行排队并分配到具有恰当技能和知识的坐席代表处，使整个呼叫处理的过程合理化。目前ACD 主要有计算机板卡、交换机两种方案,另外随着VoIP技术的发展,形成了VoIP整合的ACD方案。

本文将对ACD话务分配模型的优化进行探讨。ACD话务分配模型涉及排队论和排队模型问题。

1 排队论

排队论(QueuingTheory)，或称等候线理论(WaitingLineTheory)，是研究要求获得某种服务对象所产生的随机性聚散现象的一种数学理论和方法，它是运筹学的一个分支[3]。

排队论是20世纪初由丹麦电话工程师爱尔朗创立的。排队系统虽然千差万别，然而确有一些共同的特征，能对其进行统一的处理。这些共同的特征是：顾客为了获得某种服务而到达系统，若不能立即获得服务而又允许排队等待，则加入等待队列，获得服务后离开系统。图1为排队论模型的一般性描述。

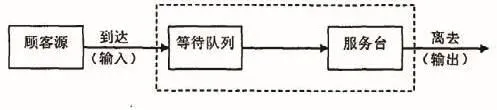
图1 排队论模型结构

任何一个排队系统都可以看作是一个随机聚散服务系统。聚表示顾客的到达，散表示顾客的离去。而随机性则是排队系统的一个普遍特点，是指顾客的到达情况(如相继到达时间间隔)与每个顾客接受服务的时间往往是无法确切知道的，或者说是随机的。排队论所研究的排队系统中，顾客相继到达时间间隔和服务时间这两个量至少有一个是随机的。由于随机因素在排队系统中的根本性影响，因此，排队论又称为随机服务系统理论。

排队系统有三个基本部分组成：输入过程、排队规则和服务机制。

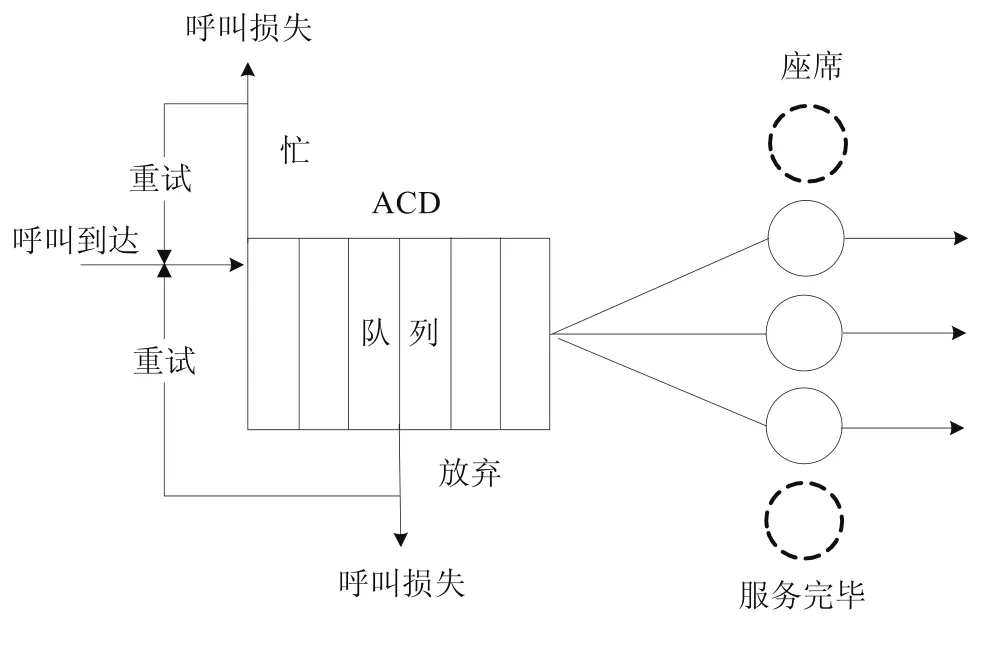
图2 呼叫中心基本排队模型

1）输入过程：顾客按怎样的规律到达，顾客源情况如何；顾客源可以是有限集，也可以是无限集。顾客的到达可以是单个的，也可以是成批的，相继顾客的到达间隔可以是确定的，也可以是随机的。

2）排队规则：指顾客在排队系统中按怎样的规则与次序接受服务；一般来说排队规则有先到先服务，后到先服务，随机服务等。

3）服务机制：指同一时刻服务台能容纳多少顾客，以及为任意顾客服务的规律。服务台可以是单个，也可以是多个，多个服务台又分为串联、并联网络等形式。服务方式有单个服务，也有成批服务。服务时间分为确定型和随机型。

按照服务机制来分，排队系统可以分为损失制、等待制和混合制三种。

1）损失制：这种系统是指排队空间为零的系统，实际上是不允许排队。当顾客到达时，若所有的服务台均被占用，则顾客自行消失。这种服务机制称为及时制。因为会失掉很多顾客，故又称之为损失制，如停车场就属于此类。

2）等待制：当顾客到达时，若所有服务台均被占用，则顾客就排队等待，这种服务机制称之为等待制。

3）混合制：该系统是等待制与损失制的结合，一般是指允许排队，但又不允许无限排下去，或者说顾客可能因为失去耐心而自行离去。

2 话务分配模型

在实践中要想通过量化指标来高效、稳定地运营和管理呼叫中心，就需要采用科学的方法对系统整体性能和ACD提供的统计数据进行分析，预测用户将要等待的时间，建立呼叫中心的排队模型。通过预测等待时间，可以平衡呼入的各队列的等待时间，提高呼叫中心的效率。呼叫中心基本排队模型可简单地抽象为图2所示的结构。

模型假设：连接到呼叫中心有k条通信线路，w为系统最大配置服务坐席数量（w≤k），N(N≤w)为提供服务的坐席数量。服务规则为先到先服务(FCFS)。

Erlang-C模型在现代呼叫中心理论分析中应用最为普遍，它的应用前提是：到达为固定速率λ的Poisson分布；服务服从服务率µ的指数分布。Erlang-C的排队模型为M/M/N/∞，W为任意顾客的等待时间；系统的负载为α=λ/µ，在等待时间服从均值为（Nµ-λ）-1的前提下，平均等待时间为：

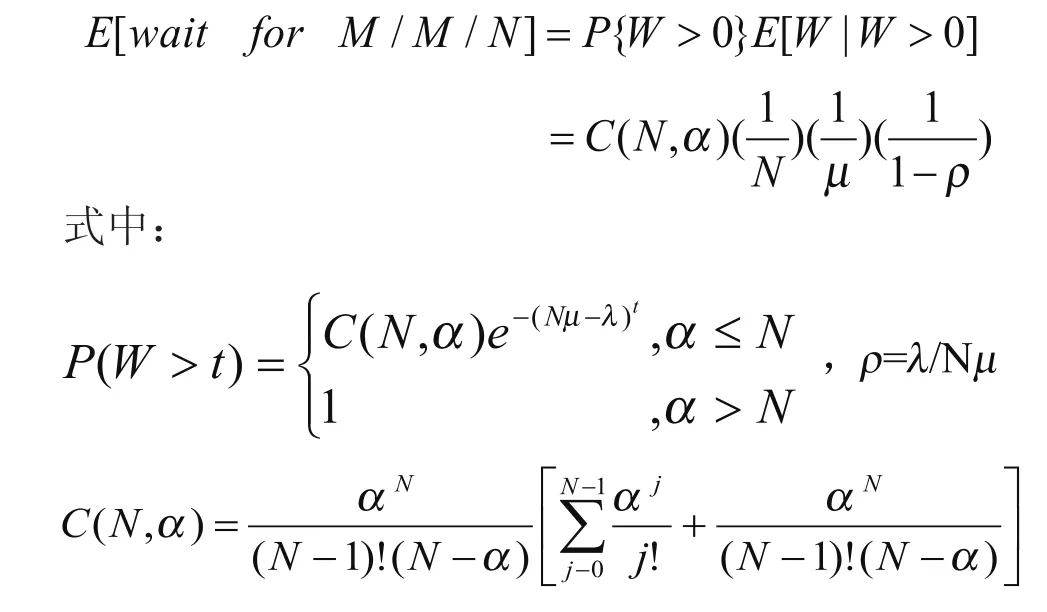
实际应用中，当Erlang-C模型应用的前提假设不满足时，预测结果跟实际结果相差很远，因此提出了改进的Poisson混合模型。到达率λ服从一个分布函数得到，在分布函数H的状态下，可得到呼叫到达X的分布形式：

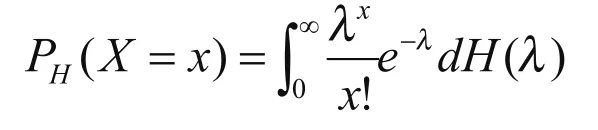
Poisson混合模型具有未知变化到达率的排队模型，采用此模型进行排队分析能更好地逼近实际系统。

Erlang-C模型、Poisson混合模型都是一种基于程控交换机系统的排队模型，队列长度和排队顺序的权重算法全部由程控交换机软件实现控制。

3 话务分配优化模型

传统ACD话务分配抽象模型有两个队列，一个是等待转接的电话队列，另一个是空闲坐席队列。如图3所示，箭头方向为最先得到服务的方向。左图显示等待转接的队列中已经有三个客户的电话等待服务，但由于没有空闲坐席为其服务，导致三个客户只有听音乐等待电话转接；右图显示等待转接的队列中已经有三个客户等待服务，空闲坐席队列有两个空闲坐席，ACD会将客户A分配给空闲坐席1，客户B分配给空闲坐席2，而让客户C继续听音乐等待。

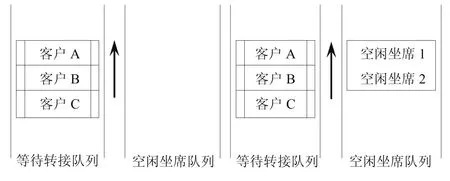
图3 基于交换机系统呼叫中心ACD话务分配抽象模型

只有当坐席结束一个接听电话后，呼叫中心系统ACD才将等待队列中第一个等待转接的电话让其出列，转接给这个当前空闲坐席接听，坐席无法主动选择接听队列中排名靠后、但比较重要的等待转接电话。

为此，我们提出了呼叫中心系统ACD话务排队的改进方式，即将转接电话排队分为物理排队和逻辑排队，物理队列还在CTI（Computer Telephony Integration）侧，而将逻辑队列放在坐席侧进行排队。当客户电话呼入时，ACD模块将电话转接消息发给所有在线坐席，坐席收到消息后，会将信息（呼入号码、学生姓名和信息）插入在本机等待转接列表中，并用声音或动态图标提示坐席有新的等待转接电话等待接听。当一个坐席按下“应答”按钮后，ACD模块将向所有坐席发出该等待转接电话出队列消息，坐席会将该电话的消息从逻辑队列中删除，保证不会有两个坐席同时接听一个转接电话。多个电话的转接消息在坐席侧依时间先后顺序排列，ACD模块允许坐席依据客户的重要性不同，有选择性地接听等待队列中的电话。

实现坐席侧排队功能，需要在ACD模块和坐席软件模块间新增一些通信控制协议、坐席软件上添加如本地电话转接表、声音、动态图标和“挂起/恢复”按钮等内容。其中“挂起/恢复”按钮是允许坐席在为电话客户服务过程中，将其电话挂起听音乐等待，坐席去应答等待队列中更急需服务的电话用户；当服务完成后，恢复挂起的电话继续为其服务。坐席恢复挂起功能时序图，如图4所示。

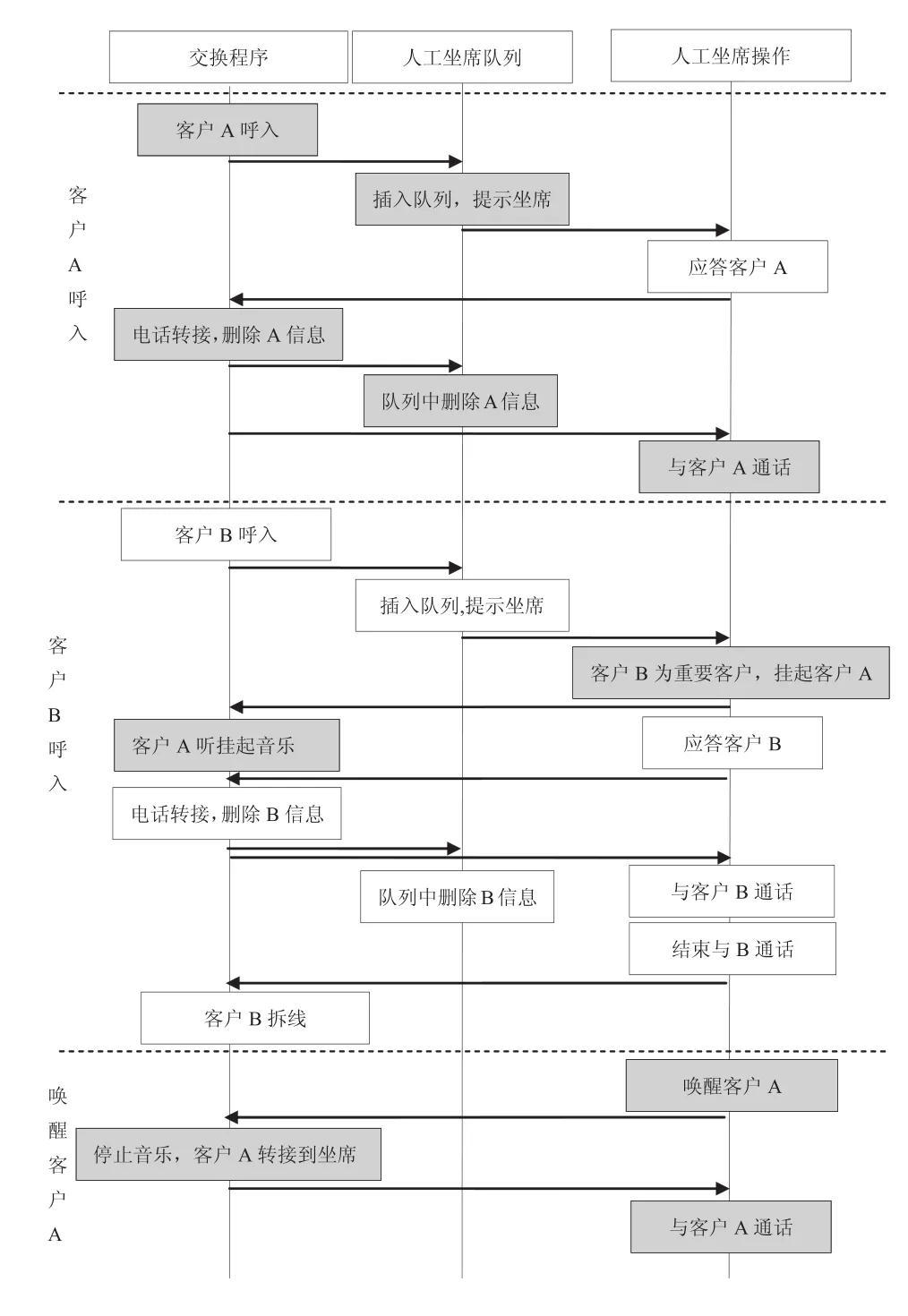
图4 坐席恢复挂起功能时序图

从上图分析可以看出，将呼叫转接队列放到坐席侧排队，实际上是将排队的物理层和逻辑层进行了有效的分离。这样分离后，在交换程序侧还需要增加一个新的物理层队列——挂起/恢复队列。坐席将一些不太重要而需要较长处理时间的电话排到这个队列里面，然后去处理队列中的重要电话，待急需处理的电话受理完毕后，再将挂起队列中的电话唤醒，然后通话。

坐席排队的优势：

1）坐席通过坐席软件能看到等待转接队列长度和等待转接的电话号码及相关信息；

2）允许坐席有选择地接听等待队列中的电话；

3）坐席的恢复/挂起功能增加了系统的处理能力。

坐席排队的缺点：

增加了交换模块和坐席模块间消息交互，使得模块间的通信协议变得更为复杂。

4 结束语

本文阐述了呼叫中心ACD话务分配模型涉及的相关技术，并提出了一种优化模型，优化后的排队模型对呼叫中心服务质量与效率权衡问题的解决提供了较好的理论基础。

[1] 肖小红,王芙蓉,黄本雄.基于CTI开放平台的呼叫中心的设计和实现[J].微型电脑应用.2001,17(3):54-58.

[2] 许娓.呼叫中心的核心技术及组成[J].电脑与信息技术.2001,(6):21-25.

[3] 陆风山.排队论及其应用[M].长沙:湖南科学技术出版社,1983,148-154.