基于Smith预估器的大时滞系统控制方法研究与仿真

东 方

（陕西国防工业职业技术学院，西安 710300）

0 引言

时滞现象常产生于化工、轻化、冶金、计算机网络通讯和交通等系统中[1,2]。就控制系统而言，时滞是指作用于系统上的输入信号或控制信号与在它们的作用下系统所产生的输出信号之间存在的时间上的延迟，当时滞较大时，将会使系统中的被调量不能及时反映控制信号的作用；另外，当被控对象受到干扰而使被调量改变时，控制器产生的控制作用不能及时有效地抑制干扰的影响，从而导致较大的超调量和较长的调节时间，甚至产生不稳定。因此，大时滞系统一直受到人们关注，成为目前过程控制研究领域的一个重要课题。

过程控制中，通常用过程纯滞后时间常数 和系统时间常数 之比来衡量过程时滞。当τ/T≤0.3时，称为一般时滞过程，过程比较容易控制，常规PID控制就能收到良好的控制效果；当τ/T＞0.3时，称为大时滞过程，需要采取特殊的高级控制方法，其控制难度随τ/T的比值增加而增加。

本文分析了在过程控制中广泛采用的大时滞过程控制算法——Smith预估补偿法，即Smith预估器，并重点讲述了其改进算法——双自由度Smith预估器，最后进行了仿真。仿真结果表明该改进算法是可行的。

1 传统Smith预估器

传统Smith预估器实质上是一种模型补偿控制，采用补偿原理，将过程对象的纯滞后环节从系统特征方程中消除，从而改善对时滞过程的控制效果。

1.1 Smith预估控制基本思路

Smith预估控制是瑞典科学家Smith于1957年提出的一种解决时滞系统控制问题的预估控制方法，其控制基本思路是预先估计出过程在基本扰动下的动态特性，然后由预估器进行补偿控制，使被延迟了的被调量提前反映到调节器，并使之动作，以此来减小超调量与加速调节过程[3]。

1.2 Smith预估控制补偿算法

引入补偿环节Gk(s)后的闭环系统方框图如图1所示。其中，Gc(s)e-τσ表示实际过程，Gk(s)表示系统一般PID调节器。

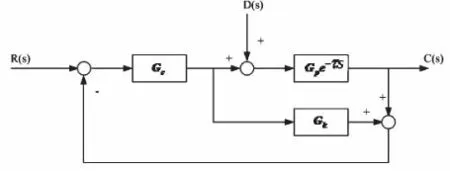
图l 引入补偿环节后的方框图

由图1可知系统闭环传递函数为

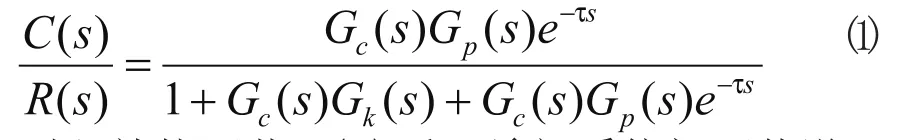
引入补偿环节Gk(s)后，希望系统闭环传递函数的分母不再含e-τσ项，即要求

将式（3）代入图1便可得到图2所示的传统连续Smith预估器方框图。其中，Gp'(s)e-τσ表示过程模型，在理想情况下，它等同于实际过程Gp'(s)e-τσ。

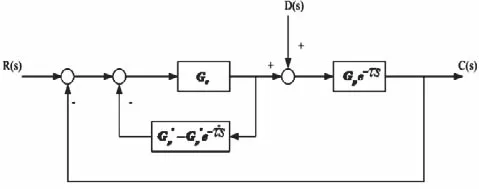
图2 传统连续Smith预估器方框图

由图2可知经Gk(s)反馈补偿后，因Gk(s)中包含Gp(s)和Gp(s)e-τσ两项，模型准确时，后一项正好与原来测量值C(s)抵消，剩下的只有控制作用通过模型 后的输出。因此，闭环系统的响应是及时的，这样就消除了纯滞后的不利影响。

2 双自由度Smith预估器

由上面的分析可知，对于传统Smith预估器，只有当模型准确时，即Gp(s)=Gp'(s)及τ'=τ时，系统才能实现完全补偿。然而，在实际系统中，由于建模误差和对象自身参数摄动等因素的影响，此条件很难满足。这是传统Smith预估器鲁棒性能差的根本原因。另一方面，系统的设定值响应和负载扰动响应都由同一个控制器Gc(s)调节，因此，控制器设计必须是对快速跟踪性能和干扰衰减性能的折衷。但由于设定值跟踪和抗干扰性能对控制器设计的要求并不一致，单控制器系统难以同时优化这两种性能指标。对于传统的Smith预估器，随着时滞的增大，这一特点表现得尤为突出。

2.1 双自由度Smith预估器结构

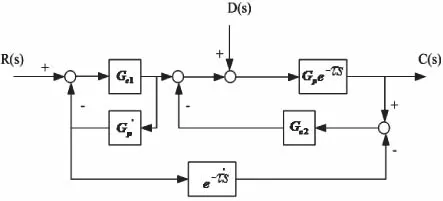
图3 双自由度Smith预估器结构示意图

采用双控制器方案，构成双自由度Smith预估控制系统，使设定值响应和扰动响应分离，从而分别设计控制器，使闭环系统同时获得良好的设定值跟踪和扰动抑制能力[4]。改进的Smith预估器结构示意图见图3，图中，Gc1(s)为设定值跟踪控制器，Gc2(s)为干扰衰减控制器。

当模型准确时，在图3中，从R(s)及D(s)到C(s)的闭环传递函数分别为

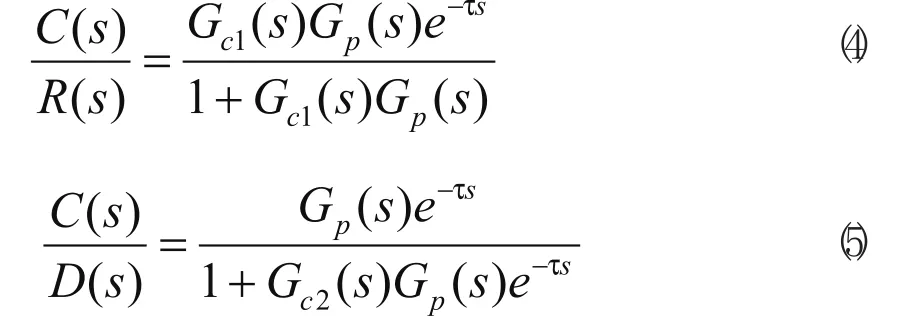
由式(4)、（5）可知，设定值响应可仅由Gc1(s)控制，并与扰动响应分离，扰动响应可只由调节。设定值响应与扰动响应的分离，使得Gc1(s)和Gc2(s)的设计可独立地进行。

2.2 控制器设计

大多数工业过程都可用一阶惯性带时滞系统来近似描述，因此，文中被控过程的数学模型设为

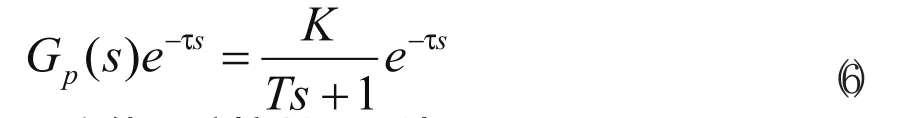
2.2.1 设定值跟踪控制器设计

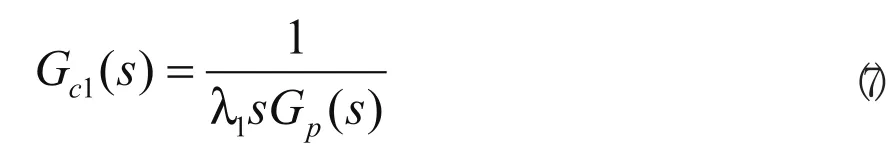
由式(7)可知，在标称情况下闭环系统总是稳定的，其响应速度由λ1决定。当λ1→0时，系统的设定值响应趋于最优。将式（6）代入式（7）便可得到控制器Gc1(s)，其为理想的PID控制器，即

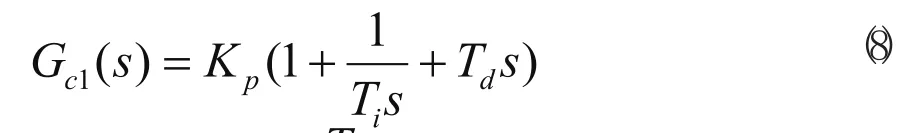
2.2.2 干扰衰减控制器设计

这里，采用与传统Smith预估器类似的方法来设计Gc2(s)。最终得到的干扰衰减控制器表达式为

式中，

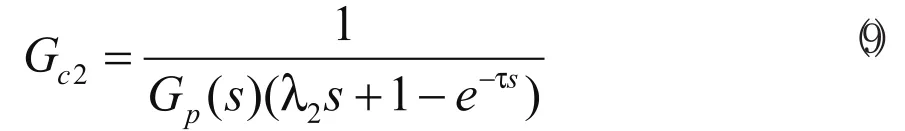
其中λ2为一可调参数，用来优化负载扰动响应。它是干扰衰减和鲁棒性能之间的折衷。当λ2→0时，系统干扰衰减性能趋于最优。

由式(9)知，控制器Gc2(s)表达式的分母中含有纯滞后项e-τσ，物理上难以实现，必须进行改进。采用1/1Pade近似或2阶Taylor级数逼近e-τσ，结合式（6），将Gc2(s)设计成近似微分PID形式

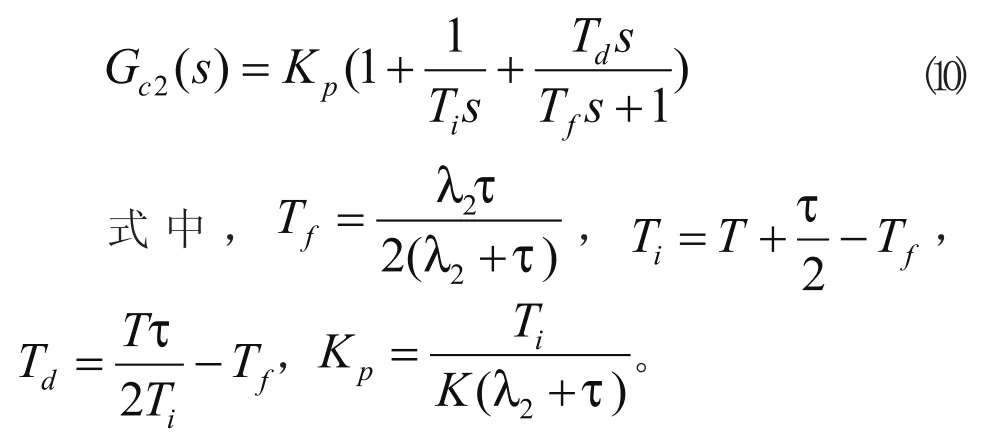
3 仿真研究

根据图2搭建的传统Smith预估控制系统方框图如图4所示，利用MATLAB对系统进行仿真。模型参数分别为K=2，T=4s，τ=4s，Gc为PI调节器，所受干扰随机成分幅度为图5为系统仿真曲线。

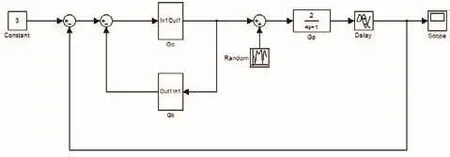
图4 传统Smith预估控制仿真模型

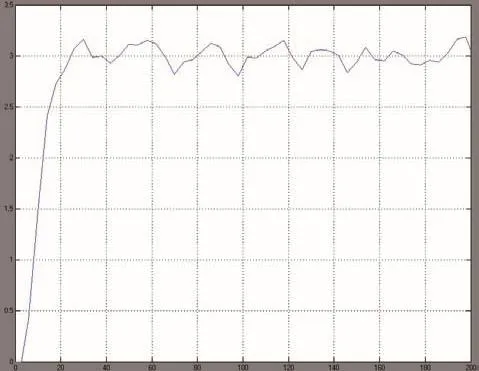
图5 传统Smith预估控制系统仿真曲线

根据图3搭建的双自由度Smith预估控制系统方框图如图6所示，利用MATLAB对系统进行仿真。模型参数分别为K=2，T=4s，τ=4s，Gc1为设定值跟踪控制器，Gc2(s)为干扰衰减控制器，所受干扰随机成分幅度为图7为系统仿真曲线。

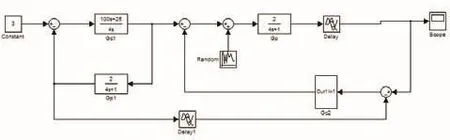
图6 双自由度Smith预估控制仿真模型

图7 双自由度Smith预估控制系统仿真曲线

4 结论

传统的Smith预估器可以获得与双自由度Smith预估器相同的设定值跟踪性能，这是因为在标称情况下二者的设定值跟踪控制回路传递函数完全相同。然而，在参数摄动情况下，两者的鲁棒性能和抗扰性能却显著不同，双自由度Smith预估器明显优于传统的Smith预估器。这一结果归因于双控制器设计方案，在理想情况下，其调节性能与无时滞时相同，只是在时间坐标上延迟了。

另外，控制器的参数整定变得简单。一旦模型确定，只须调整λ1和λ2便能获得良好的控制效果，且设定值跟踪响应和干扰衰减响应的调节可独立进行，避免了传统Smith预估器主控制器的参数整定没有统一规则，几乎靠经验的缺点。

[1] 金以惠.过程控制[M].北京:清华大学出版社,1996:l36—140．

[2] 张庆灵,张雪峰.网络控制系统研究综述与前景展望[J].信息与控制,2007,36(3):364-370．

[3] SMITH O J M.Closer control of loops with dead time[J].Che mical Engineering Progress,1957,53(2):217-219.

[4] 田玉楚.大时滞工业过程的双控制器结构[J].自动化学报,1999,25(6):824-827.

[5] 郭阳宽,王正林.过程控制工程及仿真——基于MATLAB/SIMULINK[M].北京:电子工业出版社,2009.