聚类算法在客户细分中的应用研究

郑 华

（广西工商职业技术学院，南宁 530003）

0 引言

经济的快速发展，企业的相互竞争，市场分析理论认为，20%的客户带来约80%的利润，通常情况下，只有少部分高价值的客户才能够为企业带来大部分利润。企业借助基于对客户价值的评估，同时按照企业内部各个营运小组对公司的财务贡献完成对客户的细分。通常情况下，少部分高价值的客户能够为公司带来大部分利润。进行客户细分后，公司可以为这部分客户提供足够的技术和人力资源的支持，以满足这些高价值客户对公司客户服务的期望。

对客户进行有效细分的基础是通过公司所掌握的客户数据全面地了解客户。这种通过数据推动客户细分的方法，涉及到数据库技术以及可以有效访问、分析客户信息的营销自动化应用。目前，许多公司都采用了复杂的数据挖掘工具，以便非技术型的用户也能利用大量的事务处理级数据来进行有效的客户细分。

1 聚类算法的概述

聚类是数据挖掘中的一种主要技术。将一组对象的集合分组成为由类似的对象组成的多个类的过程称为聚类。分组后得到的相同类中的对象相似，而不同类中的对象相异。聚类分析已经广泛地应用于许多领域，包括模式识别、数据分析、图像处理和市场研究。在商务上，聚类可以通过顾客数据将顾客信息分组，并对顾客的购买模式进行描述。同时，聚类分析常常作为数据挖掘的第一步，对数据进行预处理，然后用其他算法对得到的类进行进一步分析。聚类算法可以被分为划分方法、层次方法、基于密度方法、基于网格方法和基于模型方法。

1）划分方法（PAM： PArtitioning method）。首先创建k个划分，k为要创建的划分个数；然后利用一个循环定位技术通过将对象从一个划分移到另一个划分来帮助改善划分质量。典型的划分方法包括：k-means,k-medoids，CLARA(Clustering LARge Application)，CLARANS(Clustering Large Application based upon RANdomized Search)。

2）层次方法（hierarchical method）。创建一个层次以分解给定的数据集。该方法可以分为自上而下（分解）和自下而上（合并）两种操作方式。

3）基于密度方法，根据密度完成对象的聚类。它根据对象周围的密度（如DBSCAN）不断增长聚类。

4）基于网格方法，首先将对象空间划分为有限个单元以构成网格结构；然后利用网格结构完成聚类。

5）基于模型方法，它假设每个聚类的模型并发现适合相应模型的数据。

2 K-平均算法的基本思想

K均值聚类，即众所周知的C均值聚类，已经应用到各种领域。它的核心思想如下：算法把n个向量xj(1,2…,n)分为c个组Gi(i=1,2,…,c)，并求每组的聚类中心，使得非相似性（或距离）指标的价值函数（或目标函数）达到最小。当选择欧几里德距离为组j中向量xk与相应聚类中心ci间的非相似性指标时，价值函数可定义为：

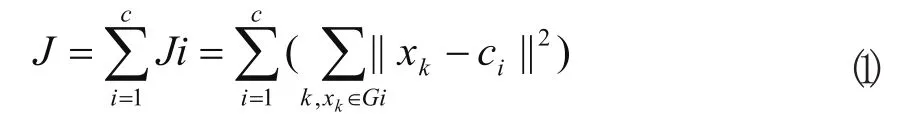
一般来说，可用一个通用距离函数d(xk,ci)代替组I中的向量xk，则相应的总价值函数可表示为：

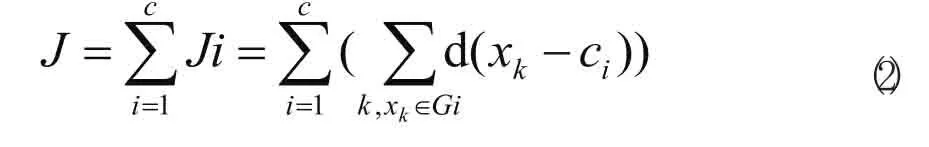
为简单起见，这里用欧几里德距离作为向量的非相似性指标，且总的价值函数表示为式(1)。

划分过的组一般用一个c×n的二维隶属矩阵U来定义。如果第j个数据点xj属于组i，则U中的元素uij为1；否则，该元素取0。一旦确定聚类中心ci，可导出如下使式(1)最小uij：

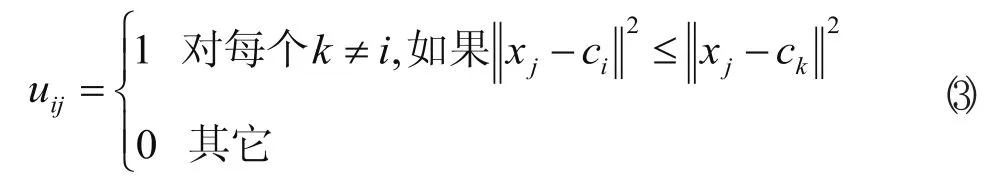
重申一点，如果ci是xj的最近的聚类中心，那么xj属于组i。由于一个给定数据只能属于一个组，所以隶属矩阵U具有如下性质：

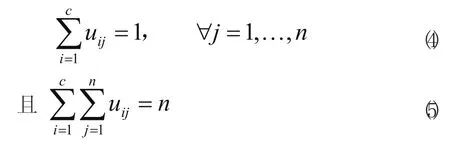
另一方面，如果固定uij则使式(1)式最小的最佳聚类中心就是组I中所有向量的均值：

为便于批模式运行，这里给出数据集xi(1,2…,n)的K均值算法；该算法重复使用下列步骤，确定聚类中心ci和隶属矩阵U：

1）初始化聚类中心ci,i=1,…,c。典型的做法是从所有数据点中任取c个点。

2）用式(3)确定隶属矩阵U。

3）根据式(1)计算价值函数。如果它小于某个确定的阀值，或它相对上次价值函数质的改变量小于某个阀值，则算法停止。

4）根据式(4)修正聚类中心。返回2）。

该算法本身是迭代的，且不能确保它收敛于最优解。K均值算法的性能依赖于聚类中心的初始位置。所以，为了使它可取，要么用一些前端方法求好的初始聚类中心；要么每次用不同的初始聚类中心，将该算法运行多次。此外，上述算法仅仅是一种具有代表性的方法；我们还可以先初始化一个任意的隶属矩阵，然后再执行迭代过程。

K均值算法也可以在线方式运行。这时，通过时间平均，导出相应的聚类中心和相应的组。即对于给定的数据点x，该算法求最近的聚类中心ci，并用下面公式进行修正：

3 聚类算法的改进

聚类是一个富有挑战的研究领域，它的潜在应用提出了各自特殊的要求。K-平均算法处理不同类型属性的能力取决于距离的计算方法，及对不同类型数据的处理，但该算法还是有以下不足之处：

1）孤立点是数据库中与数据的一般模式不一致的数据的对象。在K-平均算法中，孤立点的存在对算法结果的影响是很大的，因为迭代后的中心点是数据的平均值，如果有距离较远的孤立点，会将整个族的中心拉远，从而导致结果的偏差。

2）K-平均算法需要人工输入聚类的数目，加重了用户的负担，也使使用更为复杂化了。

通过对聚类方法的总结与比较，可以发现在已有的聚类算法中，一大类都是基于“距离”的概念，例如：传统的基于欧氏几何距离的聚类算法，常见的有K-MEANS, K-MEDIODS算法，这类算法的缺点在于处理大数据集和高维数据集时效果不好，另一方面它能发现的聚类个数常常依赖于用户参数的指定，而这对用户来说经常是很困难的。而另一类是要人们确定一些参数或者函数的，这在高维空间的数据来说是很难确定的，这类方法包括了基于密度和模型的方法。至于基于网格的方法，它的缺点就是聚类质量较差。这里我们采取一种新的思路，将基于网格和密度的方法结合起来。它的优点在于，一方面，能够自动发现包含你感兴趣知识的子空间，并将里面存在的所有聚类挖掘出来；另一方面，它能很好地处理高维数据和大数据集的数据表格。针对这种思想，人们也曾提出过一些算法，如CLIQUE，DBCA，m IGDCA等。

CLIQUE算法是一种典型的基于密度(关系)和网格(变换)的聚类方法，它利用了关联规则挖掘中的先验性质:如果一个k维单元是密集的，那么它的k-1维空间上的投影也是密集的。它的基本思想是把可k维的数据空间分成互不覆盖的矩形单元。如果一个单元中的数据点的个数大于一个阂值佣户的输入参数，则称该单元是密集的。一个cluster是指连接的密集单元的最大集合。该算法具有网格类算法效率高的优点，对数据输入顺序不敏感，可以处理高维的数据，但需要用户输入数据聚类空间等间隔距离和密度闭值参数。由于方法简化，聚类结果的精确可能降低。

受CLIQUE算法的启发，并在此算法的基础上对其进行了改进和完善。既保留了其基于网格算法的运行速度快的特点，又通过细化技术弥补了该类算法精度不高的弱点。满足了覆盖的条件，集合r中的最大区域的个数不再减少。

3.1 问题的描述

设R={Rl，R2,…，Rn}是n维立方体，其中Rl,R2…，Rn分别表示n维空间中的一个维。

算法的输入是n维空间中的点集，其中r={rl，r2…，rn}表示点集中的一个点。通过输入分割参数∮，可以将空间R的每一维分割成相同的∮个区间，从而将整个空间分成了有限个不相交的子空间，每个子空间可以表示为由n个分量组成的形式{Ul、U2…，u小其中Ui表示这一子空间中的一个维，其取值为{Ri/。/∮，Ri+1/∮}

一个子空间U的中心点UC是一个n维向量{ucl,uc2. . ..ucn} ,其中uci=(li+hi)/2。其中li和hi分别为该区间的最小值和最大值。假设一个子空间U包含k个数据点p1，p2...pk，则U的重心点PU也是一个n维向量{pul, pu2... pun}，其中PUi=(pli+P2i+...+pki)/k。

判定点r={r1，r2...rn}是否落入区间{Ul, U2,…，Un}内，主要是比较是否r的每个分量都满足Ri/∮＜=Ri＜Ri+l/∮}。在此基础上还要定义子空间u的选择率s(U), s(U)表示如下：

s(U)=(u字空间中点的个数)/(整个空间中点的总个数)

对于用户的输入参数T，如果s(U)＞ T，则称数据子空间U是密集的，反之。则是松散的。

一个聚类可以定义为，在n维空间中由一些连通的密集子空间组成的连通分支。一个n维中的子空间Ul, U2称为连通的是这样定义的：当且仅当这两个子空间只有一个公共的面或者Ul, U2都跟另一个子空间U3连通。两个子空间Ul={ u1, u2…uk}，U2={u'l、u'2…，u'k}有一个公共的面是指，存在k1个维度（不妨设这k1维就是1, 2,…，k1，有uj=u'j成立(j=1, 2,…，k)，并且对于第k维有uk＜＞u'k。

3.2 算法的设计

算法的目的在于要能够从源数据空间中自动发现这样一些子空间，使得当所有的数据记录投影到这个子空间之后，能够形成具有较高点集密度的区域。为了使得计算点密度的方法简单一些，将数据空间分割成网格状，将数据空间中的每一维划分成相同的区间数，这就意味着每一个单元具有相同的“体积”，这样单元中点的密度的计算可以转换成简单的点计数，然后将落到某个单元中的点的个数当成这个单元的密度。这时可以指定一个阀值，当某个单元格中点的个数大于该阀值时，就说这个单元格是密集的。最后，聚类也就定义为连通的所有的“密集的”单元格的集合。

3.3 算法的实现

给定一个数据集合，算法的目标是找到cluster，并标识每个数据对象所属的cluster。该算法由以下三个步骤组成：1）把数据集合中的点映射到多个单元中；2）对非密集单元移动，直到它变成密集单元或移出原来的单元范围；3）标识cluster。

下面具体说明每个步骤的方法。

1）数据空间的划分和数据集合的映射。

设置阀值T及预处理，把n维空间的每一维划分为∮个互不相交的区间，并统计每个区间单元格内的点数，即区间的密度，得到所有非空区间信息，并按维的次序作为关键字排序，存储区间位置、密度。

2）细化技术。

该步骤通过细化技术来发现新的密集区间，它的基本思想是把非密集区间向密集区间移动，从而获得更好的聚类效果。

部份源程序：

实验结果表明：改进的算法具有更好的全局寻优能力、更快的收敛速度，且其解的精度更高对初始聚类中心的敏感度降低。

4 结束语

企业的竞争重点，正在经历着从以产品为中心向以客户为中心的转移，用改进的聚类算法解决企业客户聚类分析问题，是可行的。这在支持企业决策方面有着极为重要的理论参考价值和实际应用意义，可以帮助高层管理者更好地管理企业，使企业得到更好的顺利发展。

[1] 张雷,李人厚.人工免疫c一均值聚类算法[J].西安交通大学学报,2005,39(8):836-839.

[2] 张世勇.一种新的混合粒子群优化算法[J].重庆工商大学学报:自然科学版,2007,24(3):241-245.

[3] Tang,z.h.,MaccLennan等.数据挖掘原理与应用:SQL Server 2005数据库[M].清华大学出版社,2007,(1):215-230.

[4] 刘瑜,郑平,刘莹.分析型CRM中客户细分的决策树分类技术综述[J].软件导刊.2006,(3):72-75.