在高等数学课程教学中体现数学建模思想

谭艳祥，刘仲云，梁小林

（长沙理工大学 数学与计算科学学院，湖南 长沙 410114）

如何结合高等数学教学内容培养学生的数学建模能力，从而有效地提高学生数学素质、培养学生的应用能力和创新能力，已经是当今高校数学教学的一个重要内容。数学建模教学和竞赛活动对于大学数学教学改革具有积极的推动作用，数学建模竞赛是集数学、计算机、人文修养等多方面于一体的综合测试。在高等数学课程教学中尝试将高等数学内容与数学建模方法有机结合，既加深了学生对数学知识的理解，同时也培养了学生的应用能力。高等数学的许多应用问题，实际上是一些简单的数学建模问题，只是通常高等数学教材的处理方法是作为相应数学知识的应用，按照通常数学建模的步骤和方法进行。这样一些例题虽然简单，它包含了数学建模的全过程，我们讲解时完全可以把数学建模的思想方法渗透其中。

1 在高等数学课程教学中体现数学建模思想的重要性

1）把数学建模的思想和方法融入大学高等数学课程教学中旨在推动普及数学建模思想的工作。在许多工程、物理等问题的研究中最终往往会归结到一个数学模型的问题，大面积地在高校高等数学教学中普及数学建模思想能够多学科的相互发展，达到一个良性循环的目的。

2）把数学建模的思想和方法融入大学高等数学课程教学中能提高学生数学素质、培养学生的应用能力和创新能力。

3）能够培养学生学习数学的兴趣。如果在高等数学课程教学中只是讲解一些理论上的定理的分析、证明，这不仅不能培养学生的数学兴趣反而使学生对数学课程产生了抵抗心理。反之，如果我们在高等数学课程的教学中加入一些数学建模思想的元素，从抽象的概念定理转换成具体的形象的数学模型，这样就能大大的提高学生学习数学的兴趣。

4）为全国的大学生数学建模竞赛打下了良好的基础。适时适当的在课程教学中体现数学建模的思想，不仅能完成规定的教学课程，而且能使我们的学生在无形中受到数学建模思想的熏陶，促使学生自觉的去查阅相关的书籍，为他们参加全国大学生数学建模竞赛打下了良好的数学基础。

5）能够促使学生自觉学习其它知识。数学建模是一门综合性很强的学问，其中要用到很多其它学科的知识。一旦学生对数学建模产生了兴趣，这必然使学生会自觉的去掌握其它的知识，比如计算机软件等。

2 在高等数学课程教学中体现数学建模思想的可行性

1）随着全国大学生数学建模竞赛影响力的普及，很多学生在上课时自觉要求老师在上课时讲解一些数学建模的知识。

2）高等学校的数学老师有能力在高等数学课程教学中体现数学建模思想。大部分的数学老师都曾经参加过或者指导过数学建模竞赛，对数学建模思想有相当的认识。

3）高等数学教材中有很多相关的简单的数学模型的习题。例如：①在导数以及偏导数的一些应用问题中，特别是一些求极值的应用问题；②定积分以及多元函数重积分应用的许多例题和习题；③微分方程一章的各种类型方程的应用题；④一元函数微分学的应用。这些实际上都是一些简单的数学建模问题。

3 案例分析

由复旦大学出版社出版的《高等数学》中关于一元函数微分学的应用一章有这样1个例题[1-2]：宽为2 m的支渠道垂直地流向宽为3 m的主渠道。若在其中漂运原木，问能通过的原木最大长度是多少？

3.1 模型的假设[3-5]

1）原木的直径不计（即原木的直径不可能大于渠道的宽度）。

2）不考虑渠道中水漫过渠堤。

3.2 模型的建立与求解

取O为坐标原点，支渠为x轴，主渠为y轴，建立坐标系如图1所示。A、B是通过点C（3，2）且主渠道两侧壁分别交于A和B的线段。设∠OAC=t，，则当原木长度不超过线段AB的长度L的最小值时，原木就能通过，于是建立目标函数：，由于，当时，，于是从解得：。L的最小值一定存在，而在内只有1个驻点t0，故它就是L的最小值点。于是：，故能通过的原木最大长度是7.02 m。

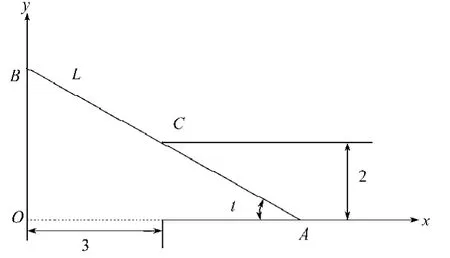
图1 支、主渠示意图Fig.1The figure of penstocks

通过以上讲解，既很好地完成了教学任务，同时同学们在如何应用数学知识建立实际问题的数学模型方面又得到了训练。

[1]庾建设.高等数学[M].上海：复旦大学出版社，2006.Yu Jianshe.Higher Mathematics[M].Shanghai：Fudan University Press，2006.

[2]同济大学数学系.高等数学[M].北京：高等教育出版社，2007.Department of Mathematics of Tongji University.Higher Mathematics[M].Beijing：Higher Education Press，2007.

[3]姜启源.数学建模[M].北京：高等教育出版社，1993.Jiang Qiyuan.Mathematical Modeling[M].Beijing：Higher Education Press，1993.

[4]阮晓青，周义仓.数学建模引论[M].北京：高等教育出版社，2005.Ruan Xiaoqing，Zhou Yicang.An Introduction to Mathematical Modeling[M].Beijing: Higher Education Press，2005.

[5]韩中庚.数学建模方法及其应用[M].北京：高等教育出版社，2005.Han Zhonggen.Mathematical Modeling and Its Application[M].Beijing：Higher Education Press，2005.