多目标投资组合模型的理想点解法

陈国华，廖小莲

（湖南人文科技学院 数学系，湖南 娄底 417000）

1952年，Harry Markowitz提出了证券组合投资均值-方差模型，它为现代证券组合投资理论奠定了基础[1]，国内外许多学者依据这些理论对证券组合投资进行了深入的研究，采用不同的方法得出了一系列的研究成果[2-4]。严应超等[5]以我国证券市场上2种基本的金融资产股票和债券为例进行了具体的实证分析，得出了多目标投资组合模型要优于单一目标投资组合模型的结论。本文以总体风险损失率作为投资组合的风险度量，以换手率刻画流动性，建立了多目标投资组合模型。鉴于多目标规划问题绝对最优解通常是不存在的，本文采用理想点法对模型进行求解，并给出了实际算例。

1 多目标投资组合模型的建立

在现代投资组合理论中经常使用多目标投资组合模型，王梦东等在文献[6]中引入了偏好参数 ，将多目标问题转化为单个目标的二次规划问题，既能弥补以前的模型缺陷，又能寻找到更好的解法来获得有效投资组合；肖冬荣等[7]在Markowitz的均值方差投资组合模型的基础上引入偏度水平，并用伸缩指标相应做出均值、方差和偏度3个模糊目标，形成一类新的非线性多目标投资组合模型；周洪涛等在文献[4]中将模糊集合的概念引入投资组合模型中，并将多目标投资组合模型中的收益、方差和偏度3个目标模糊化，建立了模糊多目标投资组合模型，并提出了一个动态遗传算法求解；王俊等[8]根据信息论中熵的概念，提出用熵来度量投资组合对风险的分散能力，同时提出了兼顾收益、风险、熵的多目标投资组合模型，并用改进的经典遗传算法求解该模型。

在证券投资决策理论中，投资收益和投资风险被认为是投资者所关心的2个主要因素。然而，在证券投资实践中，证券的流动性也不能忽视。证券的流动性是指证券的变现能力，目前度量证券流动性的方法较多，其中广为使用的方法主要有：交易股数、交易笔数、交易金额、换手率和流通速度。换手率是股票成交量（或成交额）与流通盘（或流通市值）的比值，它充分反映了股票的流动性[9]。本文以换手率来刻画流动性，建立带流动性的多目标投资组合模型（MADL）如下：

第j种证券的收益率为随机变量Rj，预期收益率为；

2 多目标组合线性优化模型的求解

由于MADL是一个多目标线性规划问题，其绝对最优解通常是不存在的。证券组合投资决策的实质是寻求MADL的Pareto有效解，相应的证券组合称为有效的。多目标规划已有较多的解法[10]，基本方法有：主要目标法、分层序列法、评价函数法、理想点法、线性加权法等。本文中采用理想点法求解，理想点解法的优点是能根据投资者相应的满意程度得到满意的投资组合，其具体做法如下：

1）分别求下面3个规划问题的最优解和最优值

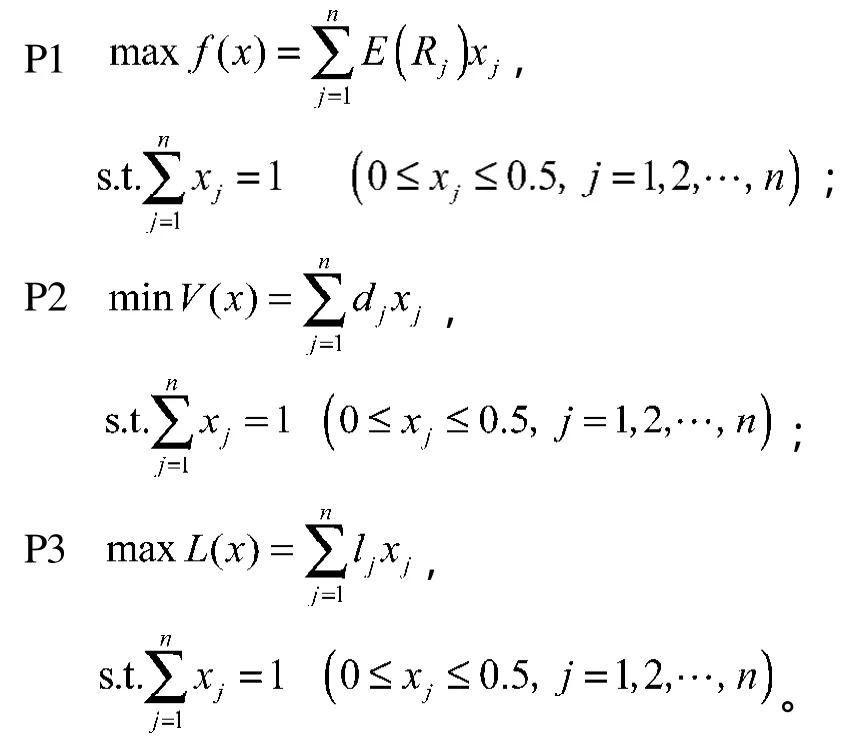
设P1，P2，P3的最优值分别为f *(x)，V*(x)，L*(x)，最优解分别为x(1)，x(2)，x(3)，则理想点为

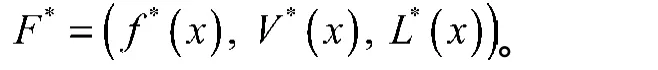
2）检验理想点，如果x(1)=x(2)=x(3)，绝对最优解为x*=x(1),否则，求单目标最优化问题的最优解。

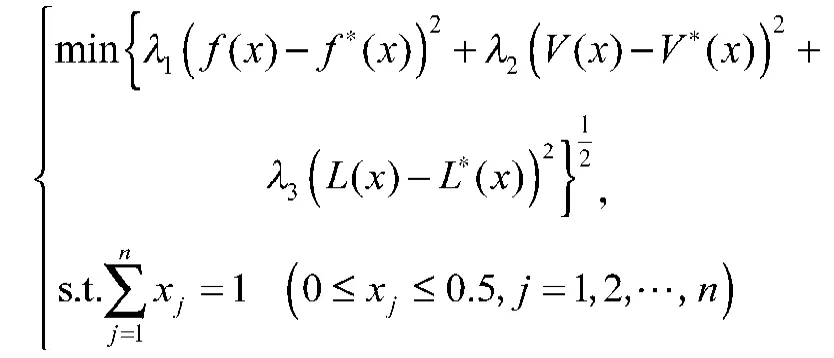
3 数值算例

设已知9种股票2005年01月～2006年06月的月收益情况如表1所示，日平均换手率为参考换手率，见表2，通过Excel的计算，求得9种股票的预期收益率及，见表3、4。

表1 9种股票2005年01月～2006年06月的月收益情况Table 1Monthly earnings of 9 kinds of stock in January 2005 ～ June 2006

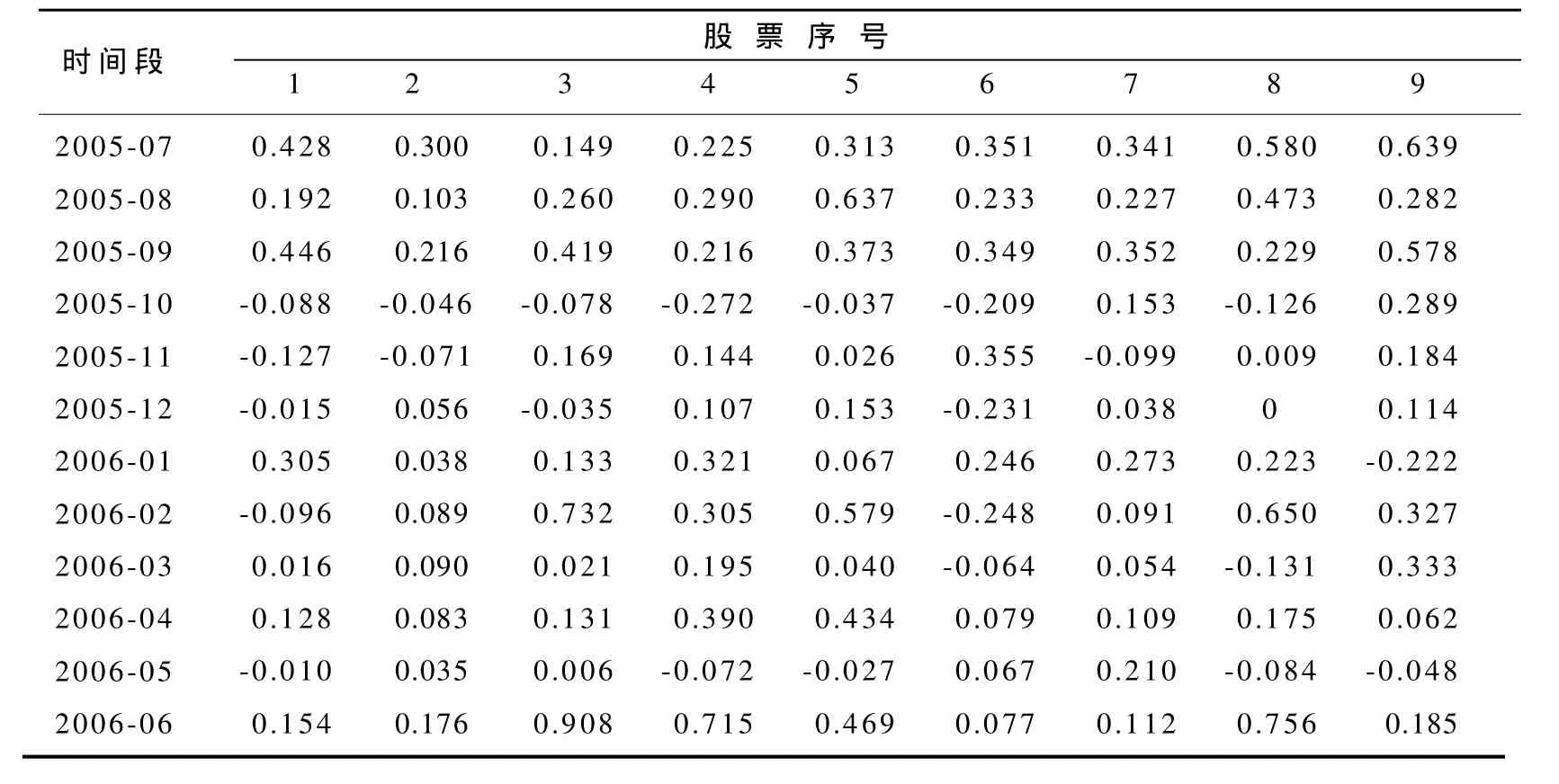
续 表

表2 9种股票2005年01月～2006年06月的日平均换手率Table 2The daily average turnover rate of 9 kinds of stock in January 2005 ～ June 2006

表3 9种股票的预期收益率Table 3The expected return rate of 9 kinds of stocks

表4 9种股票的Table 49 kinds of stocks

表4 9种股票的Table 49 kinds of stocks

股票序号dj 1 0.189 4 2 0.089 6 3 0.211 1 4 0.234 7 5 0.302 5 6 0.177 8 7 0.130 9 8 0.315 3 9 0.225 0

利用理想点法的最短距离算法求解，得到理想点F=(0.194，0.000 11，0.118 5)，其中，f(x)的极小点x1*=(0,0,0,0,0.5,0,0,0.5,0)T，V(x)的极小点x2*=(0,0,0,0,0.5,0.5,0,0, 0)T，L(x)的极小点x3*=(0,0,0.5,0,0.5,0,0,0,0)，因为x1*与x2*和x3*都不同，下面求单目标最优化问题：

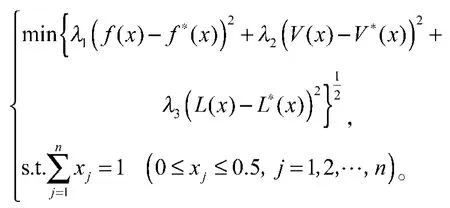
4 结语

本文将投资组合预期收益极大化和投资组合绝对偏差和（风险）极小化作为目标，建立了一种多目标证券组合投资模型。鉴于多目标规划问题绝对最优解通常是不存在，本文采用理想点法求解，给出了数值算例，说明了模型的可行性。

[1]Markowitz H.Portfolio Selection：Efficient Diversification of Investments[M].New York：Wiley，1959.

[2]Konno H，Yamazaki H.Mean-Variance Deviation Portfolio Optimization Model and Its Applications to Tokyo Stock Market[J].Management Science，1991，37(5)：519-531.

[3]Cai X Q，Teo K，Yang X Q，et al.Portfolio Optimization under a Minimax Rule[J].Management Science，2000，46：957-972.

[4]周洪涛，王宗军，宋海刚.基于模糊优化的多目标投资组合选择模型研究[J].华中科技大学学报：自然科学版，2005，33(1)：67-69.Zhou Hongtao，Wang Zongjun，Song Haigang.A Multi-Objective Portfolio Selection Model Based on Fuzzy Optimization[J].Journal of Huazhong University of Science and Technology：Nature Science Edition，2005，33(1)：67-69.

[5]严应超，张传新.多目标投资组合研究[J].全国商情（经济理论研究），2008(2)：80-81.Yan Yingchao，Zhang Chuanxin.Research on Multi-Objective Portfolio[J].National Trade (Economic Theory)，2008(2)：80-81.

[6]王梦东，童仕宽.基于二次规划的多目标投资组合模型[J].武汉理工大学学报，2007，29(8)：171-174.Wang Mengdong，Tong Shikuan.Multi-Objected Investment Combination Model Base on Quadratic Programming[J].Journal of Wuhan University of Technology，2007，29(8)：171-174.

[7]肖冬荣，黄 静.基于均值、方差和偏度的投资组合模糊优化模型[J].统计与决策，2006(7)：37-38.Xiao Dongrong，Huang Jing.Based on the Mean，Variance and Skewness Portfolio Model by Fuzzy Optimization[J].Statistics and Decision，2006(7)：37-38.

[8]王 俊，叶中行.一种改进的实数型遗传算法在多目标最优投资组合选择中的应用[J].宁夏大学学报，2004，25(3)：1-4.Wang Jun，Ye Zhongxing.An Improved Real-Valued Genetic Algorithm in Multi-Objective Optimal Portfolio Selection[J].Journal of Ningxia University，2004，25(3)：1-4.

[9]苏冬蔚，麦元勋.流动性与资产定价：基于我国股市资产换手率与预期收益的实证研究[J].经济研究，2004(2)：95-105.Su Dongwei，Mai Yuanxun.Liquidity and Asset Pricing：An Empirical Exploration of Turnover and Expected Returns on Chinese Stock Markets[J].Economic Research Journal，2004(2)：95-105.

[10]解可新，韩立信，林友联.最优化方法[M].天津：天津大学出版社，1997：218-265.Xie Kexin，Han Lixin，Lin Youlian.Optimization[M].Tianjin：Tianjin University Press，1997：218-265.