一类非线性组合系统新的稳定性条件

刘 烨，刘建州

（湘潭大学 数学与计算科学学院，湖南 湘潭 411105）

0 引言

自20世纪60年代以来，许多作者从不同角度对非线性大系统的稳定性和镇定问题进行了研究[1-9]。如文献[1-2]构造了Lyapunov函数，用Lyapunov方法来检验线性大系统的稳定性。文献[3]给出了不用Lyapunov函数的判定准则，但其判定方法还要涉及到子系统的稳定性，因此结果趋于保守。文献[4]通过对微分方程解的估计，导出了具有时变时滞系统的时滞无关的稳定性条件，却没有考虑系统的非线性扰动和不确定性因素，且要求子系统是稳定的。文献[5]利用比较原理和M矩阵特性导出了非线性组合系统稳定的充分条件，其假设是非线性和不确定性部分具有范数界，仅用一数值界去刻画，结果具有一定的保守性。文献[6]讨论了不确定非线性子系统经不确定非线性互联而成的组合大系统，给出了可分散反馈镇定的充分条件，其前提是一隐式矩阵方程有解，但一般情形下这一矩阵方程的解是不存在的。

本文在已有研究基础上，讨论了一类非线性组合系统的稳定性问题，获得了新的稳定性判定准则，这一准则还放宽了已有文献对系统不确定性和非线性的要求条件，并对系统的反馈镇定问题也具指导作用。

1 问题描述

考虑由N个子系统构成的非线性组合大系统

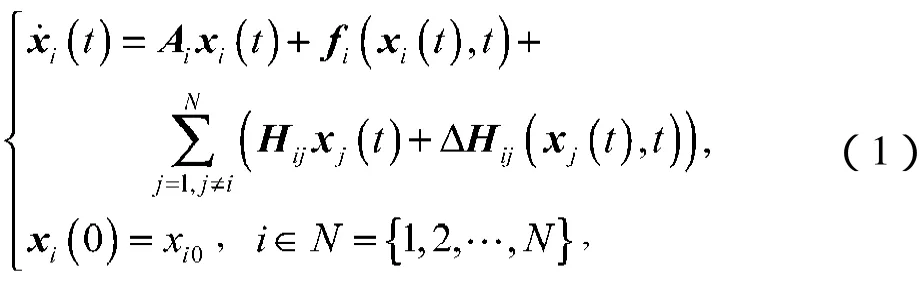
对系统（1）做以下假设：

假设1 非线性部分

式（2）中：Di为具有非负对角元的对角矩阵；。

假设2 关联不确定性

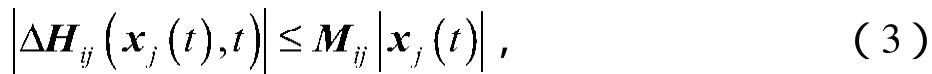
式（3）中：Mij为具有非负对角元的对角矩阵；。

注1 以往大多数文献要求非线性和不确定性满足匹配条件或具有范数界，但仅用一数值界去刻画非线性部分和不确定性，往往导致结果趋于保守，而本文用一向量这样具体模型去描述，比已有文献的限制条件都弱，可使后面的分析过程和结果更为精确。

2 主要结果

将式（4）代入式（1）中，得到

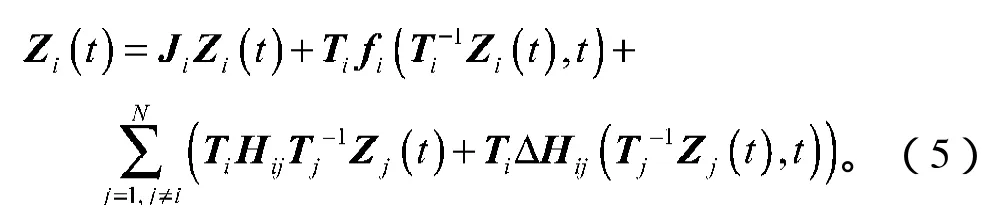
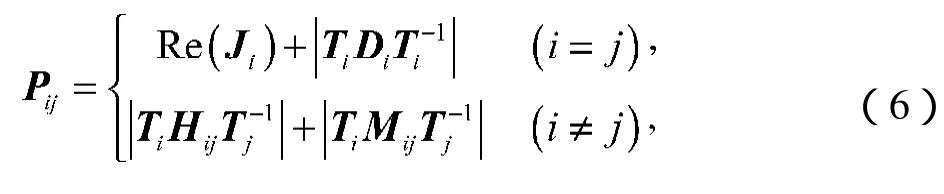
证明 由微分方程的基本性质可知方程式（5）的解为

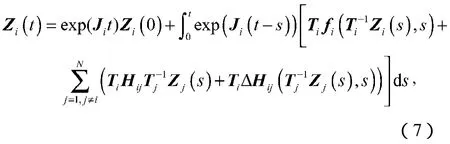
进一步，可得到下面的不等式

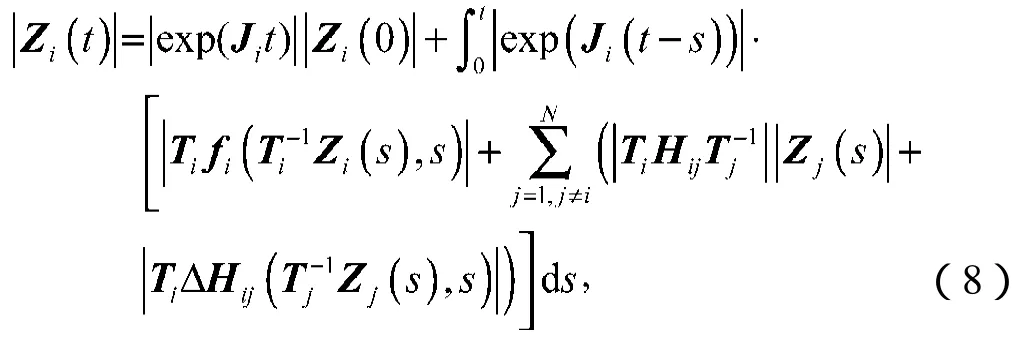
然后，利用假设1和2条件可得

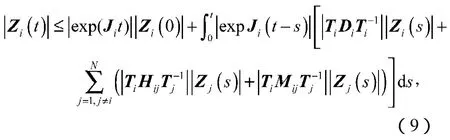
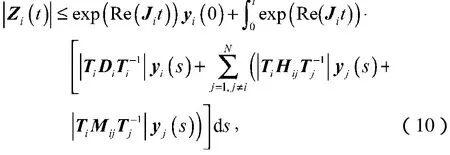
显然，上式右端是下面微分方程（11）的解

3 数值实例

考虑如下由2个含不确定性的子系统组成的关联系统：

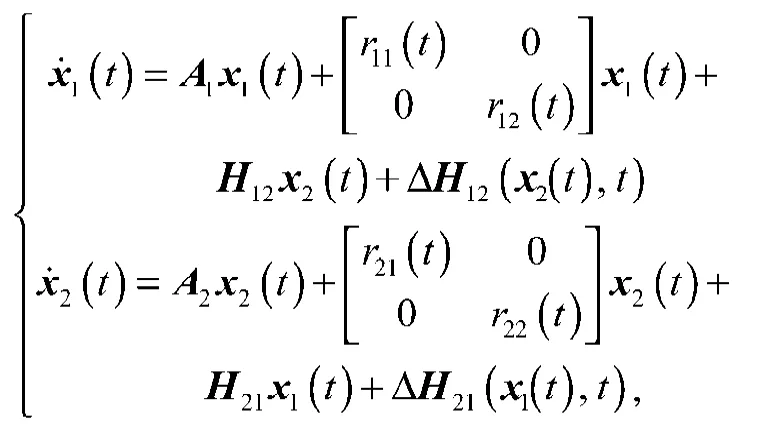
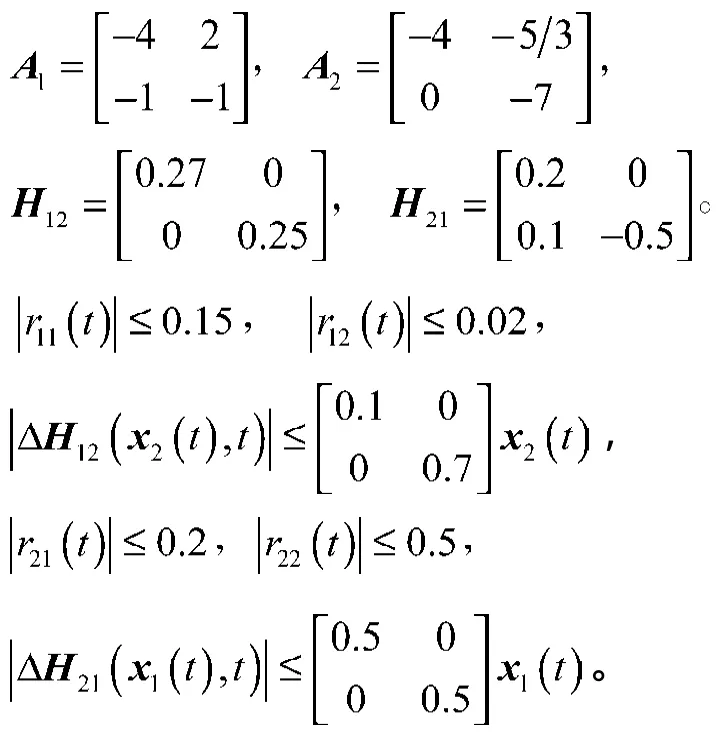
解经计算得

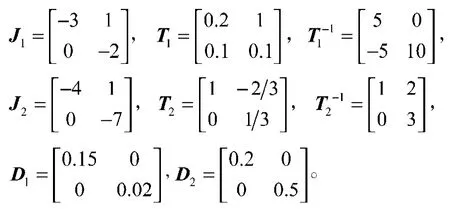
由计算结果知：

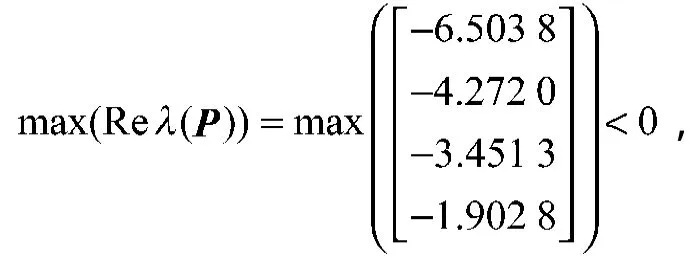
同时可看出，P为负M矩阵，故此系统为渐近稳定的。

此例中的非线性部分和不确定性便不是用范数界（一数值界）去估计的，更没有要求匹配条件。

4 结语

本文以定理1的形式给出了关于系统（1）的稳定性判定准则，其优点在于运用该准则可避免构造Lyapunov函数，其要求的假设条件比已有文献所要求的均宽松，在推导过程中运用该准则可使结论更为精确，且不涉及子系统的稳定性。此外，本文的结果还可用于非线性组合大系统鲁棒分散镇定的研究。

[1]Bailey F N.The Application of Lyapunov's Second Method to Interconnected Systems[J].SIAM Journal on Control and Optimization，1965，3(3)：443-462.

[2]Matrosor V M.Method of Lyapunov Vector Functions in Feedback Systems[J].Aut.Remote Cont，1972，33：1458-1469.

[3]盖如栋，井元伟，张嗣瀛.一类非线性组合大系统的稳定性[J].自动化学报，1997，23(1)：73-76.Gai Rudong，Jing Yuanwei，Zhang Siying.Stability of A Class of Nonlinear Large Scale Composite Systems[J].Acta Automatica Sinica，1997，23(1)：73-76.

[4]周少武，张志飞，谭 文，等.具有时变时滞大系统的新的稳定性条件[J].湘潭矿业学院学报，2001，16(4)：81-83.Zhou Shaowu，Zhang Zhifei，Tan Wen，et al.A New Sufficient Condition for Stability of Large-Scale Systems with Time-Delay[J].Journal of Xiangtan Mining Institute，2001，16(4)：81-83.

[5]张志飞，苏彩虹，章 兢.基于比较原理的非线性组合大系统的输出反馈镇定[J].控制与决策，2007，22(7)：836-840.Zhang Zhifei，Su Caihong，Zhang Jing.Output Feedback Stabilization for Composited Nonlinear Systems Based on Comparison Principle[J].Control and Decision，2007，22(7)：836-840.

[6]Yan X G，Zhang S Y.Decentralized Output Feedback Robust Stabilization for A Class of Nonlinear Interconnected Systems[J].IEEE Trans Automatic Control，1998，43(2)：294-299.

[7]Zhang Siying.Study on Symmetric and Similar Structures of Complex Control Systems[J].Journal of Qingdao University，2001，14(4)：3-6.

[8]Chen Ning，Gui Weihua，Cai Zixing.Decentralized Robust H∞Control for Uncertain Large-Scale Systems Using Linear Matrix Inequalities[J].Journal of Central South University of Technology，2003，34(6)：72-76.

[9]年晓红，李鑫滨，杨 莹，等.Lurie控制系统的关联绝对稳定性一双线性矩阵不等式方法[J].控制理论与应用，2005，22(6)：999-1004.Nian Xiaohong，Li Xinbin，Yang Ying，et al.Bilinear Matrix Inequality Approach to the Absolute Stability of Interconnected Lurie Control Systems[J].Control Theory & Applications，2005，22(6)：999-1004.