基于瞬时电感电流控制的无线并联逆变系统

鞠洪新 邹昭平 梁 海

（北京自动化技术研究院 北京 100009）

1 引言

纵观过去的几十年，逆变电源并联技术在诸多工业领域中发展迅速，国内外的许多专家学者对此提出了各种各样的控制策略，其中大部分可以归类为有联络线的并联模式。有联络线模式的并联理论相对简单，实现容易，因而在逆变电源并联技术发展早期得到了普遍认同。但是有联络线并联模式也存在着非常明显的缺点，比如并联单元的地理位置受到限制、电磁干扰严重、冗余性不佳等。正是因为有联络线控制技术这些无法克服的先天性缺点，从而催生了逆变电源的无线并联模式，并促进着无线并联控制技术的快速发展。

常规的无线并联系统，通常采用功率下垂理论进行并联控制[1-2]。该理论近似认为逆变电源输出阻抗呈感性，忽略了其阻性分量对系统输出功率的影响，因而可能造成并联控制上的不准确性。鉴于此，本文设计了一种数字化无线并联逆变系统，该系统采用基于电感电流反馈的逆变电压瞬时双闭环控制结构，对系统的输出阻抗特性加以改善，使其在输出电压的基波频段呈现感性，从而保证了功率下垂理论的正确应用。并联时只要将逆变单元输出交流母线并接，各单元就能依据自身的输出功率，通过合理、有效、优化的控制算法来调节各自的输出电压指标，从而实现并联单元之间的负载合理分配。

2 传统功率下垂理论及其局限性

以两台逆变电源并联运行为例，在考虑输出滤波器影响的条件下，由于逆变电源输出阻抗呈感性，且线路阻抗远小于它，则该并联系统等效电路可近似简化如图1所示。

图1 两逆变电源并联等效电路Fig.1 The equivalent circuit of two parallel inverters

依图1可以得到各逆变单元的输出有功功率Pi和无功功率Qi分别为[3-4]

式中 Xi——逆变电源输出电抗；

δi——逆变电源输出电压iE˙与并联系统输出电压E˙间的夹角。

由式（1）可以看出，在系统输出电压一定时，逆变单元可以通过检测本单元的输出功率大小，根据自身容量把频率（相位）与幅值两个要素通过输出的有功功率和无功功率进行近似解耦控制。传统的并联控制常引入电压-频率下垂特性，使各逆变电源的输出电压频率和幅值均按下式变化[5-6]：

式中 ω0——逆变电源空载输出电压角频率；

E0——逆变电源空载输出电压幅值；

m——逆变电源输出角频率的下垂系数；

n——逆变电源输出电压的下垂系数；

P，Q——逆变电源的输出有功功率、无功功率；

ω ——逆变电源输出的电压角频率；

E——逆变电源输出的电压幅值。

采用这种传统的功率下垂理论虽然能够实现逆变电源的稳定并联，但它忽略了系统输出阻抗中阻性成分对功率特性的影响。然而在实际系统中，逆变电源输出阻抗还与系统的控制策略有关，它除了包含感性分量外，还不可避免地含有一些阻性成分[7]，例如：并联系统的线路阻抗，输出滤波电感的等效串联阻抗，功率器件的开关寄生阻抗等，难于测量和估计。

设r为逆变电源等效输出阻抗中的阻性分量，ωL为其感性分量，即系统输出阻抗Z=r+jX=r+jωL，则令ωL1= ωL2= ωL，r1=r2=r，由图 1可以推导出考虑r影响的逆变电源并联系统功率模型表达式

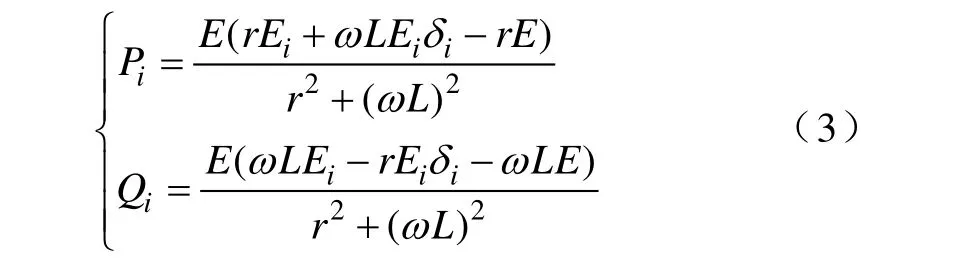
从式（3）中可以看出，受r影响，逆变电源并联系统各单元的输出功率与其输出电压相位和幅值都不是单一的对应耦合关系，各单元输出电压幅值和相位不一致都会造成其输出有功功率和无功功率的差异，从而导致系统产生环流。当系统输出阻抗仅含阻性分量时，逆变电源输出电压和功率的对应关系会发生根本改变，不再依照式（1）变化。而前述的传统下垂理论则忽略了有功功率、无功功率与输出电压相角、幅值之间的两两耦合关系，直接依据有功功率调节输出电压相位，依据无功功率调节输出电压幅值，这种控制显然是不够准确的。

3 系统拓扑与控制结构

本系统中各并联逆变单元的主电路均采用电压型全桥逆变主电路，逆变桥的后级经L-C滤波器来滤除输出电压中的高次谐波，其拓扑结构如图2所示，其中滤波电容的等效串联电阻没有考虑。图中Vdc为系统直流输入电压，VT1～VT4为功率开关器件IGBT模块，L和C为系统输出滤波电感和电容，rL为滤波电感的等效串联电阻，R是系统的负载。

图2 逆变单元的主电路拓扑Fig.2 The main circuit topology of inverter unit

早期逆变电源单机的数字控制，由于受微处理器的速度限制，大多采用输出电压的有效值反馈。但这种控制策略难于消除死区以及非线性负载等因素引起的低次谐波，从而带来严重的输出电压波形畸变。另外，系统若仅采用输出电压的有效值反馈控制，对各种扰动的调节还会有周期延时，而这些对于动态性能要求非常高的逆变电源无线并联系统来说，都是非常不利的。因此，本文采用输出电压/电流瞬时双闭环控制策略，内环是电感电流瞬时调节环，用以提高系统的动态性能；外环是瞬时电压控制环，用于改善系统输出电压的波形，使其具有较高的输出精度。同时，由于电感电流是电流调节器输出与电感作用的积分结果，因而采用电感电流反馈不仅具有很好的跟踪性能，而且还有内在的限流保护功能。系统瞬时双闭环控制框图如图3所示。

图3 逆变电源瞬时双闭环控制结构框图Fig.3 Block diagram of inverter with the instantaneous double close loop controller

4 电感电流控制对输出阻抗的改善[8]

以图2所示单相逆变电源的主电路拓扑结构来分析，可以得到该系统的主电路状态微分方程为

式中，D为功率器件的开关状态控制变量，其取值有1、0和-1三态。

合并式（4）、式（5），得系统输出电压动态模型

根据图 3，含有前馈调节的系统输出电压瞬时双环复合控制结构的简化框图如图4所示。

图4 基于电感电流反馈的简化控制结构Fig.4 Block diagram based on inductive current control

由图4可得

联立式（6）、式（7）两式即得基于电感电流反馈的系统闭环线性化动态模型

由电路的二端网络定义知，逆变电源系统可以建立如下等效电路模型

式中 G(s)——逆变电源电压放大倍数；

Zo(s)——逆变电源输出阻抗。

比较式（8）和式（9），可以得出基于电感电流反馈的逆变电源输出阻抗表达式，记为Zo(s)

为了更好地说明电感电流反馈在输出阻抗方面的优越性，将其与电容电流反馈控制做比较，图 5是基于电容电流反馈的简化控制结构。与图4相比可以看出，两图控制结构唯一不同的是电流反馈量变为了电容电流，即为Csvo。

图5 基于电容电流反馈的简化控制结构Fig.5 Block diagram based on capacitive current control

由图5可得

联立式（6）、式（11）可得基于电容电流反馈的系统闭环线性化动态模型

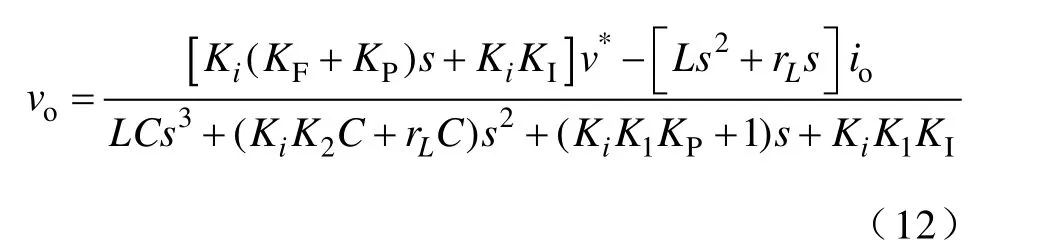
同理可以得出基于电容电流反馈逆变电源的输出阻抗表达式，记为o()Zs′

比较Zo(s)和o()Zs′可以看出，若控制K2Ki≫rL，则基于电感电流反馈的逆变电源输出阻抗中rL对系统输出阻抗的影响就可以被大大减弱，而基于电容电流反馈的逆变电源输出阻抗则不具备此特性，从系统输出阻抗的对数幅频和相频曲线图也可以清楚地看出这一点。

图6所示为 rL分别取0.1、0.3、0.5Ω时，系统的输出阻抗博德图，其中图6a采用的是电感电流反馈，而图6b采用的是电容电流反馈。

图6 系统输出阻抗博德图Fig.6 The Bode plot of system output impedance

从图6b中可以清楚地看到，在频率较低的范围内，基于电容电流反馈的逆变系统输出阻抗的幅频和相频曲线趋向均依赖于 rL的大小；而图 6a则表明，基于电感电流反馈的逆变系统输出阻抗的幅频和相频曲线却几乎不受其影响，在基波频段严格呈感性，满足传统功率下垂理论的应用条件。rL的存在虽然给系统的设计和控制带来了很多不利影响，但采用瞬时电感电流反馈能够较好地解决此问题。

5 实验结果

依照上述控制思想，本文研制了采用数字信号处理器TMS320LF2407A主控的1kW并联逆变电源样机。主电路滤波电感为1mH，滤波电容为30µF，直流输入电压250V，交流输出为110V/50Hz。控制参数为：K1=0.005，K2=0.016，Ki=1963.5，KF=0.285，KP=9.27，KI=28 344。

图7是两台逆变电源并联带载运行时的稳态输出电压电流波形图，其中ch1表示逆变电源1的输出电流，ch3表示逆变电源2的输出电流，ch2表示并联系统输出电压，ch4表示并联系统输出电流，数学计算信号M则表示系统环流。图7a中，系统带阻性负载并联运行时，两台逆变电源的输出电流峰值为 6.95A、6.57A；图 7b中，系统带非线性整流桥负载时，两台逆变电源的输出电流峰值分别为7.44A，6.32A。

图7 系统带载稳态输出波形Fig.7 System steady state waveforms with a load

从图7可以看出，两台逆变电源带阻性负载和非线性负载并联运行时，采用本文控制策略实现的并联系统对负载电流的均分控制效果很好：在基波频段呈现电感特性，在谐波频段呈现电阻特性，从而整个并联系统的输出稳态电压压降不大，输出环流约小于10%。

图8为两台逆变电源动态并联时的系统输出电压电流波形图，其中图8a为一台逆变电源正常运行时，另一台并联并入的波形图，图8b为两台逆变电源正常并联运行时，一台退出的波形图。从图中可以看出：图 8a中当 1#逆变电源未并入系统时，2#逆变电源输出电流即为负载电流，当1#逆变电源并入后，2#逆变电源输出电流经过几个周期的调节后减小，两台逆变电源各自承担负载电流的 1/2；图8b中两台逆变电源正常并联工作时，两台逆变电源各自承担负载电流的 1/2，当 1#逆变电源推出系统后，2#逆变电源输出电流就迅速增大，直至整个并联系统的负载电流。两组实验表明，无论哪种动态变化过程，整个系统的负载电流和输出电压波形正常，系统响应迅速、负载均分效果良好。

图8 两台逆变电源的动态并联波形Fig.8 Dynamic state waveforms of the parallel inverters

6 结论

本文设计的基于电感电流控制的无线并联逆变系统，采用功率下垂理论，避免了各并联单元间的一切控制互连线。同时通过与基于电容电流反馈的控制方案相比较指出，该控制器在基波频段能够克服系统输出阻抗中阻性成分对系统控制的影响，从而保证了传统功率下垂理论的正确应用。文末的实验结果证明了控制方案的有效性与可行性。

[1]Bekiarov S B, Emadi A. Uninterruptible power supplies: classification, operation, dynamics, and control[C]. Applied Power Electronics Conference and Exposition 2002, APEC’02, Seventeenth Annual IEEE,2002: 597- 604.

[2]Coelho E A A, Cabaleiro P, Donoso P F. Small-signal stability for parallel-connected inverters in standalone AC supply systems[J]. IEEE Trans. on Industry Applications, 2002, 38(2): 533-542.

[3]Mukul C Chandorka, Deepakraj M Divan, Rambabu Adapa. Control of parallel connected inverters in standalone AC supply systems[J]. IEEE Transactions on Industry Applications, 1993, 29(1): 136-143.

[4]邱关源. 电路[M]. 3版. 北京：高等教育出版社，1989.

[5]何利铨，邱国跃. 电力系统无功功率与有功功率控制[M]. 重庆：重庆大学出版社，1995.

[6]Guerrero J M, Vicuna L G de, Matas J, et al. A wireless controller to enhance dynamic performance of parallel inverters in distributed generation systems[J]. IEEE Transactions on Power Electronics,2004, 19(5): 1205-1213.

[7]曾建友， 陈息坤，等. 逆变器输出阻抗对并联运行环流影响的研究[J]. 电力电子技术，2003，37(3)：21-24.Zeng Jianyou, Chen Xikun, et al. Study of influence of inverter output impedance on circulating-current in parallel operation[J]. Power Electronics, 2003, 37(3):21-24.

[8]Guerrero J M, Vicuna L G de, Matas J, et al. A high-performance DSP-controller for parallel operation of online UPS systems[C]. Applied Power Electronics Conference and Exposition 2004, APEC’04,Nineteenth Annual IEEE, 2004, 1: 463-469.