R/S分析在水库流域降水变化趋势预测中的应用

陈崇德，唐东明

（湖北省漳河工程管理局，湖北 荆门448156）

1 概述

漳河水库是以灌溉为主，兼有防洪、城市供水、发电、水产养殖、旅游、航运、生态环境保护等多目标运用的大型水利工程，总库容21.19亿m3，其中兴利库容9.24亿m3，调洪库容4.24亿m3。从运用实践看，水库多年平均缺水量为3.01亿m3，若遇干旱或特大干旱年，则需水缺口更大。因此，水资源数量明显不足是该水库的一大问题。由于R/S分析对时间序列具有预测功能，故根据水库来水变化的历史实测资料，利用R/S分析的原理和方法，对未来水库水资源的丰枯变化趋势进行分析，对指导水库的调度运用有较大的作用。

2 计算方法

R/S分析法（Rescaled Range Analysis，重新标度极差分析法）是由英国学者赫斯特（H.E.Hurst）在总结尼罗河的多年水文观测资料时，于1965年提出的一种处理时间序列的方法，它在分形理论中有着重要作用［1］。R/S分析法计算简单，其基本原理与方法如下：

2.1 计算均值

设时间序列{X（t）}，t=1，2，…，n，对于任意正整数τ≥1，定义均值序列则：

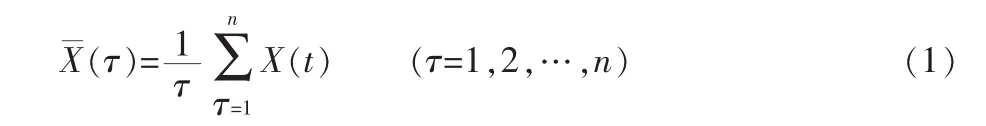
2.2 计算累积离差

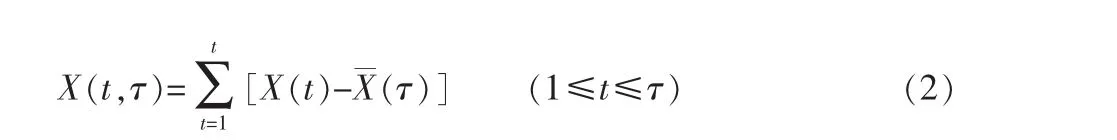
2.3 计算极差序列

2.4 计算标准差序列

2.5 计算比值

式中 α为常数；H为Hurst指数。

由式（5）得：

根据时间序列{X（t）}，利用最小二乘法，可得式（6）的直线回归方程，则直线的斜率即为H指数。

水库年来水量的丰枯变化在时间轴上表现为不连续点分布，是一种不规则的Cantor集合，即来水量具有时间分形结构。为了对水库来水变化趋势进行预测分析，采用分布式布朗（Fractional Brownian motion）模型。设有一“粒子”在X轴上随机游动，它每一时间间隔τ向左或向右移动的步长为X，那么X的分布函数密度为:

式中 G为扩散系数。

又设{X1，X2，…，Xn}为步长序列，是一个独立同分布的时间序列，经过n步行走后，“粒子”在X轴上的“位置”为:

式（8）为布朗函数，经过简化计算得到相关函数γ（t）：

由式（9）可知，当H=1/2时，γ（t）=0，即为一般的布朗运动；当H≠1/2时，γ（t）≠0，即为分式布朗运动。Mandelbrot将H指数推广为0＜H＜1。

为了预测未来的水库来水趋势Xn+1，则式（1）可得：

令R（n+1）/S（n+1）=［α（n+1）］H=K，并将式（3）、（4）代入式（10），可解得：

式中 A=（n+1）［（n+1）2-nK2］

最后将X（τ）代回式（7），即可得未来水库来水量变化趋势Xn+1。

3 应用实例

湖北省漳河水库已有1957～2008年52a的实测水库降水资料，多年平均降水量989.6mm，若将年降水量大于1100mm称为丰水年，则自1957年以来，共出现过15个丰水年（见表1），若把1956年作为计算零点，那么得到的时间序列为（将1989年以后的资料留作验证之用）：

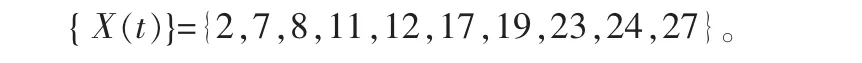
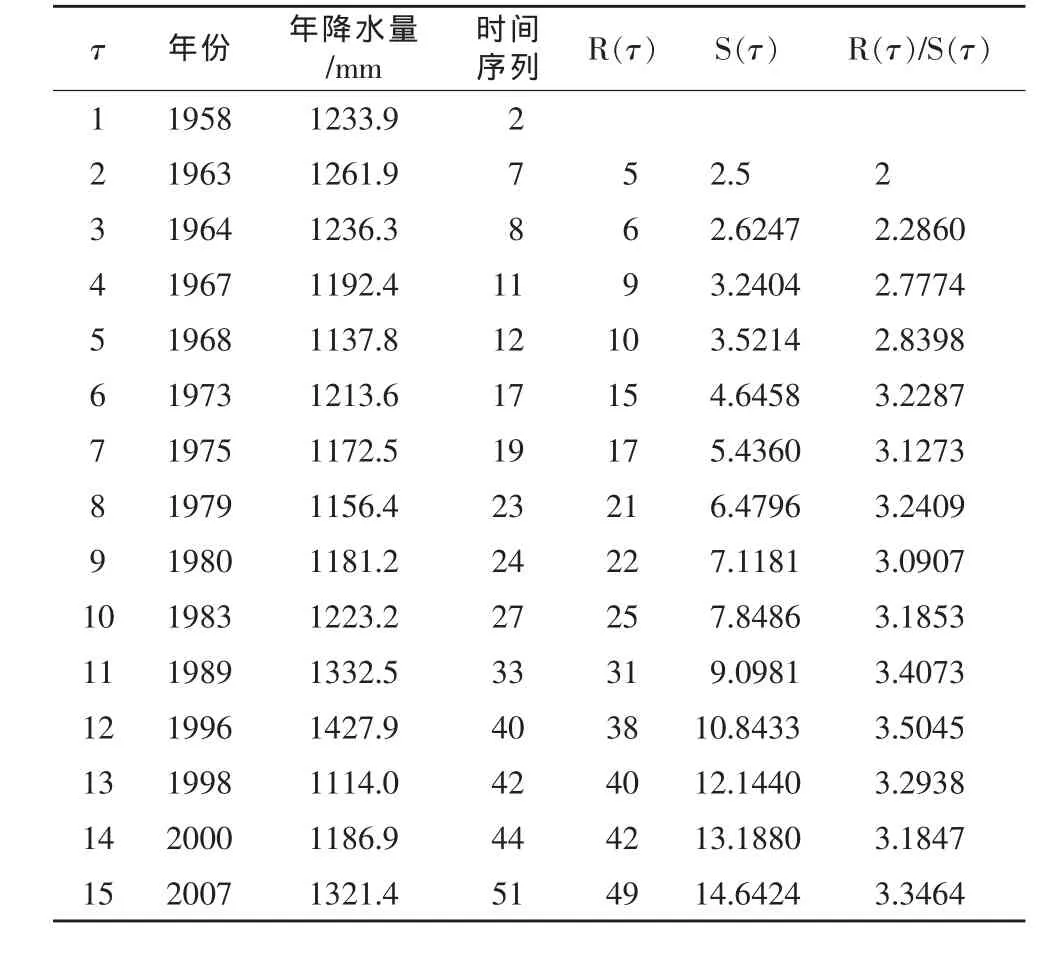
表1 漳河水库降水量大于1100mm的年份及R（τ）/S（τ）计算

经过计算，可得到H、α及R（τ）/S（τ）的关系式，从预报效果来看，虽然整个过程都是严格的数学推导过程，但有部分年份计算结果不太理想。究其原因，一是丰水年出现的时间序列并非是真正意义上的布朗运动［3］；二是误差是客观存在的，如预测下一个丰水年的K值，是以平均值代替的，且模型容纳误差的能力不够；三是H指数的计算是通过双对数回归分析得到的，这个结论的可靠性有多大，其显著性如何，以及如何修正，目前缺少有效的分析评价方法。但通过对历史资料的模拟，发现误差还是有一定规律，即随着资料系列的延长，误差呈减少的趋势，且误差范围比较稳定（见表2）。

表2 误差统计

将误差项代入公式（10）：

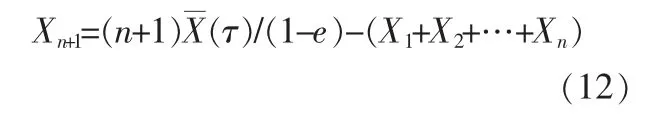
式中 e为误差率。

经计算，H=0.3155，α=2.3294，相关函数γ（11）=-0.2257≠0（属于分式布朗运动），则：

根据公式（11）、（12）计算，漳河水库下一个丰水年为γ11=33.43≈33，计算零点还原后，即1956+33=1989年。1989年实际降水量为1332.5mm＞1100mm，故预测正确。将1989年信息加入{X（t）}，得到新的时间序列：

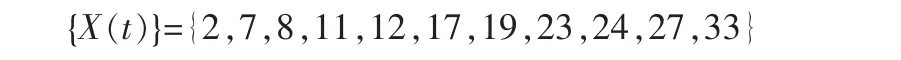
经计算，H=0.2968，α=2.3294，相关函数γ（12）=-0.2455≠0（属于分式布朗运动），则：

根据公式（11）、（12）计算，漳河水库下一个丰水年为X12=39.69≈40，计算零点还原后，即1956+40=1996年。1996年实际降水量为1427.9mm＞1100mm，故预测正确。将1996年信息加入{X（t）}，得到新的时间序列：

经计算，H=0.2779，α=3.6647，相关函数γ（13）=-0.265≠0（属于分式布朗运动），则：

根据公式（11）、（12）计算，漳河水库下一个丰水年为X13=41.9≈42，计算零点还原后，即1956+42=1998年。1998年实际降水量为1114mm＞1100mm，故预测正确。将1998年信息加入{X（t）}，得到新的时间序列：

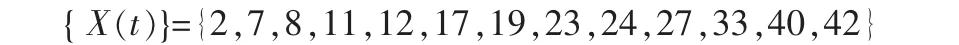
经计算，H=0.2521，α=5.5063，相关函数γ（14）=-0.2908≠0（属于分式布朗运动），则：

根据公式（11）、（12）计算，漳河水库下一个丰水年为X14=43.99≈44，计算零点还原后，即1956+44=2000年。2000年实际降水量为1186.9mm＞1100mm，故预测正确。将2000年信息加入{X（t）}，得到新的时间序列：

经计算，H=0.2281，α=8.8221，相关函数X（15）=-0.3140≠0（属于分式布朗运动），则：

根据公式（11）、（12）计算，漳河水库下一个丰水年为X15=50.99≈51，计算零点还原后，即1956+51=2007年。2007年实际降水量为1321.4mm＞1100mm，故预测正确。

4 结语

目前，R/S分析方法在水库年来水趋势预测中成功应用的例子还不多，有些问题还没有得到有效解决，但并不影响该方法的有效使用［3］。 大量研究结果表明［4-11］，水文系统是一个复杂的巨系统，水文要素的时空变化具有高度的非线性特点。R/S分析是自仿射分形衍生出来的时间序列分析方法，对于非线性具有统计特性的数据系统，采用R/S分析法可以很好地揭示其变化过程的内在规律性，并可对其分形特征进行定量描述。应该指出的是：尽管应用了分形和R/S分析理论中的概念、方法进行预测，但仍无法减小或消除系统的内在随机因素而造成的不可预报部分，如观测资料的误差（噪声影响）等，因此进一步探索洪水发生的规律，改进模型，提高模型的稳定性，对于提高洪水的预见期和预测精度是很有意义的。

［1］马岚，魏晓妹.石羊河下游年径流序列的变异点分析［J］.干旱地区农业研究.2006，24（2）:174-177.

［2］张利平，王德智，夏军，等.R/S分析在洪水变化趋势预测中的应用研究［J］.中国农村水利水电，2005（2）:38-40.

［3］邹新月，许涤龙.M指数估计方法的有效性检验［J］.统计研究，2004（8）:37-39.

［4］江田汉，邓莲堂.Hurst指数估计中存在的若干问题［J］.地理科学，2004，24（2）:177-182.

［5］于延胜，陈兴伟.R/S和Mann-Kendall法综合分析水文时间序列未来的趋势特征［J］.水资源与工程学报，2008，19（3）:41-44.

［6］樊毅，李靖，仲远见，等.基于R/S分析法的云南干热河谷降水变化趋势分析［J］.水电能源科学，2008，26（2）:24-27.

［7］徐宗学，李占玲，史晓崑.石羊河流域主要气象要素及径流变化趋势分析［J］.资源科学，2007，29（5）:121-127.

［8］凌超.中国股票市场的非线性结构实证研究［D］.武汉：华中科技大学，2006.

［9］李琴.乌鲁木齐近50年的气候变化分析［D］.乌鲁木齐：新疆大学，2006.

［10］张晓伟，沈冰，孟彩侠.和田绿洲水文气象要素分形特征与R/S分析［J］.中国农业气象，2008，29（1）:12-15.