基于支持向量回归机的汽轮机转子应力修正系数模型

方 宁, 纪冬梅, 姚秀平, 程超锋, 杨 宇, 史进渊

(1.上海电力学院能源与环境工程学院,上海200090;2.上海发电设备成套设计研究院,上海200240)

随着国民经济的发展和科学技术水平的提高,我国的火力发电机组正在向高参数、大容量、高效率的方向发展,参数与容量的提高对机组运行的安全性和可靠性都提出了更高的要求.转子是机组中最重要的部件之一,在机组中起着工质能量转换及扭矩传递的作用,转子是否正常工作决定着整个机组运行的安全性和可靠性.在汽轮机运行时,高、中压转子处于高温蒸汽中并高速旋转,转子不仅承受着叶片、叶轮、主轴本身离心力所引起的巨大应力、蒸汽的轴向推力以及由于温度分布不均匀引起的热应力,而且还要承受巨大的扭转力矩和轴系振动所产生的动应力,工作条件非常恶劣.同时,随着大容量火力发电机组的不断投入运行以及用电结构的巨大变化,电网中“峰谷差”的现象日益严重,电网中的超临界发电机组也要参与调峰运行,机组的频繁启停以及长时间的变工况运行将加剧转子的寿命损耗.为了延长机组的寿命,必须对启停及负荷变化等过程中转子的应力进行在线监测和控制.

1 汽轮机子转子应力的计算

由于汽轮机转子在高速下旋转,鉴于目前的技术水平,还不能对转子的温度及热应力进行直接可靠地测量,只能按照传热学和弹性力学原理建立数学模型,通过计算的方法来获得.

1.1 应用常规方法在线计算转子应力

目前常用的汽轮机转子应力计算方法主要是有限元法和一维简化计算方法.利用有限元法对汽轮机转子进行应力分析时,因转子是一个均匀、各向同性且无内热源的物体,属于轴对称非定常温度函数问题,可以使用轴对称分析,先建立转子的有限元模型,然后进行网格剖分并确定求解的边界条件,对于汽轮机高压转子前轴封第一弹性槽槽底圆角处、调节级后侧叶轮根部过渡圆角及轴肩处等结构比较复杂的部位,还要进行二次细网格划分,这样有助于更好地了解这些部位在机组启动下的温度场及应力分布.在计算转子的温度场时,转子表面与蒸汽间热交换的边界条件(第三类边界条件)hf(tf-tw)=λ(∂t/∂r)Г是求解温度场的必要条件,包含在边界条件中的放热系数目前还没有统一的计算公式,比较常用的计算公式可以参考文献[1].转子的热应力计算基于温度场,当求出瞬态温度场后,在时间域内选出若干时间节点的温度场计算转子的应力.

有限元法虽然可以精确地计算汽轮机转子在启动状态下的热应力,但是由于要建立转子有限元模型并进行剖分离散,整个计算过程比较复杂,而且单元和结点数目较多,在实际应用当中存在着计算时间较长的问题[2-4].

简化计算方法将转子视为无限长圆柱体,只考虑转子的径向温差,而忽略轴向热流的影响,并将转子材料的物性参数及蒸汽对转子表面的放热系数作为常数处理,根据不稳定导热方程求得温度分布和应力[5-6].简化计算方法虽然可以快速地计算转子的应力场,但精度不高.

1.2 应用神经网络方法在线计算转子应力

为了克服应力计算中有限元法及简化法存在的缺陷,一种可行的方法就是将简化计算方法应用于在线计算,然后对计算出来的转子等效应力进行修正,以提高其计算精度.该方法的具体技术思路为:对于同型号汽轮机的同一转子,给定相同的蒸汽、压力、转速和功率等参数变化曲线,分别采用简化法和有限元法计算出转子外表面某一关键应力监测点的等效应力σ和σeq,然后将2种计算方法得到的应力结果进行比较,得出应力的修正系数 β=σ/σeq,再利用回归方法计算任一状态下的修正系数.这样既可以发挥简化法计算快捷的特点,又可以通过修正计算提高应力在线计算的精度[7].

为了应用预先获取的有限数目工况的应力修正系数来推知实际运行中可能出现的任意一工况下的应力修正系数,以往多采用传统神经网络的方法,但实际应用情况表明:传统的神经网络在样本数量有限的情况下不能保证学习机的性能,当样本数据较少时,容易出现“过学习”现象,算法的推广能力较差.20世纪90年代,在机器学习领域出现了一种新的学习方法——支持向量算法,该算法专门适用于有限样本情况下非参数的估计问题,现已成为机器学习和数据挖掘领域的标准工具.

2 支持向量回归算法

支持向量算法是在统计学习理论的基础上提出的一种全新的学习方法,该方法的最大特点是以结构风险最小化原则取代传统学习方法中的经验风险最小化原则,在解决有限样本学习问题方面具有很好的泛化能力,目前在模式识别、函数逼近和概率密度估计等机器学习问题中都有着较广泛的应用[8].

解决回归问题的支持向量法又称为支持向量回归算法(support vector regression,SVR),该法可以表述为:给定训练集,T={(x1,y1),(x2,y2),…,(xn,yn)}∈(X×Y)n,其中:xi∈X=Rn,yi∈Y=R,i=1,…,n.在线性函数集F={f(x,a)=(w◦x)+b}中寻找回归函数 f(x,a0),使得损失函数L(y,f(x,a))在训练集上最小.为保证解的稀疏性和回归结果的鲁棒性,通常会忽略真实值在某范围内的误差,该类型的函数称作ε不敏感损失函数:

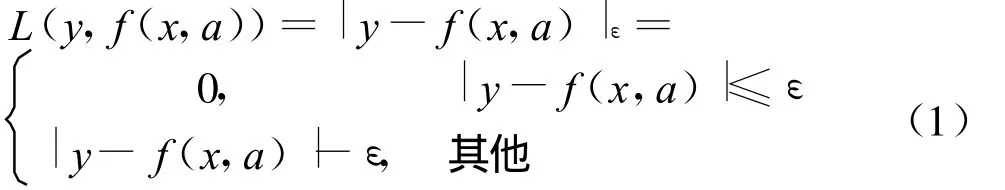
式中:y为真实值;f(x,a)为预测值.

根据支持向量机的结构风险最小化原则,引述结构风险函数:

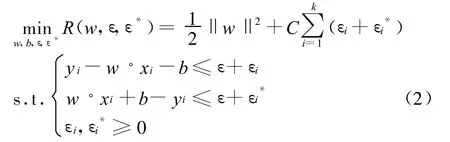
式(2)中右边第一项是描述回归函数 f(x,a0)复杂度的项,称为结构风险,回归函数越平坦,泛化能力越好,为了控制回归函数的复杂度,应使‖w‖2尽量小;右边第二项为训练样本产生的经验风险,规则化常数(C＞0)是对超出误差ε的样本的惩罚程度进行控制,也称惩罚系数,其作用是在经验风险和结构风险(模型复杂度)之间取一折中点,C越大,则对训练数据的拟合程度越高,但泛化能力越差 ;εi,≥0为引入的松弛因子,是为了使式(2)的解存在.然后根据最优化理论中非线性规划最优解与拉格朗日函数鞍点的关系,可求得问题的最优解,再根据对偶原理转化为式(3)求其最大点.

式(3)中K(xi,xj)是满足Mercer定理的内积核,ai≠对应的数据点定义为支持向量.核函数可以将非线性的自变向量转换到高维特征空间,最后在高维特征空间内进行线性函数拟合,以实现原问题的非线性回归估计.虽然通过非线性变换可将样本数据映射到高维甚至无穷维空间,并在高维空间中构造最优分类超平面,但在求解最优化问题和计算分类平面时,并不需要计算该非线性函数,甚至不需要知道其具体形式,而只需计算K(xi,xj).

3 汽轮机转子应力修正系数的支持向量回归机模型

3.1 模型输入量与输出的选择

支持向量回归机网络基本上可以分为3层:输入层、核函数及输出层.网络的输入层即目标问题的影响特征因素;中间层为核函数,可以根据解决问题的实际需要进行构造;输出层为目标问题,即模型的回归结果.

在汽轮机启动状态下,高中压转子主要承受热应力与机械应力,而这两种应力的影响因素比较复杂,所以在确定模型输入时,应综合考虑特征因素,特征因素过多或过少均会严重影响神经网络模型的泛化性能.通过对应力影响因素的分析,并考虑现场的实际监测条件,最终选取主蒸汽压力、主蒸汽温度、转速、转子平均温差(转子体积平均温度与转子外表面温度之差)、机组负荷、汽缸内表面温度、前1～5 min汽轮机主蒸汽温度及负荷的变化率、前6～14 min汽轮机主蒸汽温度及负荷的变化率等10个参数作为模型的输入,应力修正系数作为模型的输出[7].

3.2 模型参数及核函数选取

支持向量回归机的模型参数主要有惩罚系数C、不敏感系数和核函数的待定参数[9].C值的大小决定着由训练样本产生的经验风险对模型的影响,当C值减小时,经验风险也随之减小,若C值过于微小,则由于没有得到大量的训练数据信息,建立的模型也就失去了解决具体问题的能力.不敏感系数的值反映了模型对数据中噪声幅度的容许界限,也反映了支持向量机对数据噪声水平的预测和对数据点的逼近程度.核参数宽度系数对支持向量回归机的学习过程起着关键作用,选择合适的宽度系数,将使支持向量回归机避免过学习现象.

模型参数采用交叉验证结合人工搜寻的方法进行选取,首先将训练数据分为10份,其中9份作为训练数据集,而另外的1份作为验证数据集,用验证集来验证所得回归数据的误差,循环10次,直到10份数据全部被选择一遍;然后利用人工搜寻的方法对交叉验证得到的模型参数进一步优化.

支持向量算法常用的核函数有:线性核函数、多项式核函数、径向基核函数和Sigmoid核函数.由于影响汽轮机高中压转子应力修正系数的因素非常复杂,而且这些因素之间也存在着强烈的耦合,所以最终选取径向基函数:k(x,y)=exp{-(‖x-y‖2/σ2)}作为模型的核函数,该核函数可以很好地解决复杂的非线性回归问题.

3.3 应用实例及分析

综合以上分析,以某超临界600 MW机组高压转子为例,建立基于支持向量回归机的汽轮机高中压转子应力修正系数模型.

首先采用等直径实心圆柱的简化模型和有限元模型计算出高压转子调节级叶轮根部圆角部位在冷态启动、温态启动、热态启动和极热态启动过程中的等效应力,将2种应力计算结果进行比较,从而得到一定数量的修正系数样本数据;然后随机选取一半的样本数据作为训练样本,利用支持向量回归机建立应力修正系数的神经网络模型,为了避免数据溢出现象,训练之前对样本中的特征因素数据进行标准化处理,余下的样本数据用来对模型的性能进行验证.为了与一般神经网络进行对比,本次研究也利用径向基函数网络(RBF)对转子应力修正系数进行了建模.图1～图4所示为利用2种神经网络模型得到的在冷态启动、温态启动、热态启动和极热态启动下应力修正系数测试样本的回归结果.

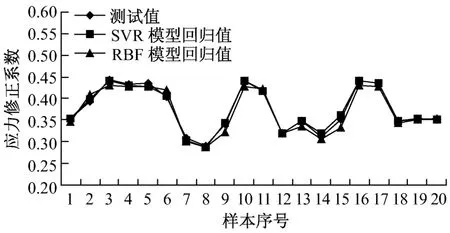
图1 冷态启动下修正系数回归值与测试值的比较Fig.1 Comparison between reg ression value and measurement during a cold start-up

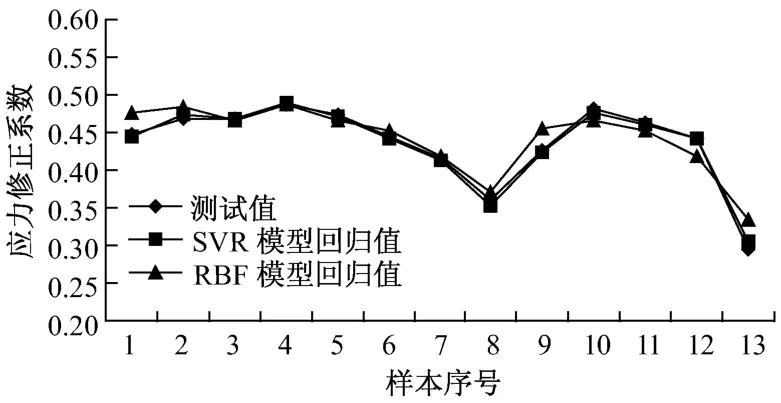
图2 温态启动下修正系数回归值与测试值的比较Fig.2 Comparison between reg ression value and measurement during a warm start-up

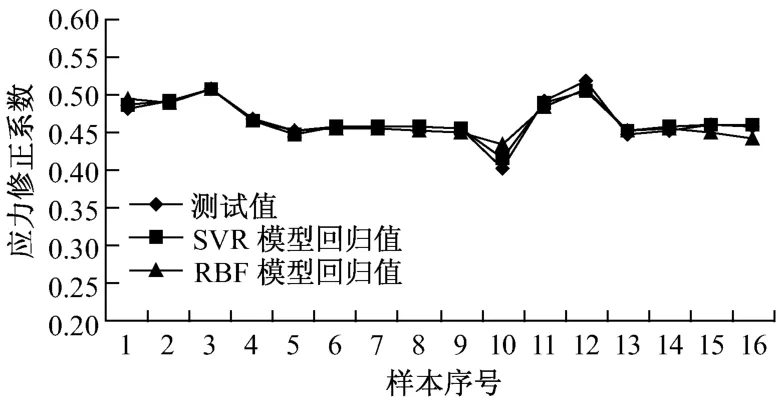
图3 热态启动下修正系数回归值与测试值的比较Fig.3 Comparison between reg ression value and measurement during a hot start-up

图4 极热态启动下修正系数回归值与测试值的比较Fig.4 Comparison between reg ression value and measurement during an extremely hot start-up

从图中可以看出,在4种不同的启动状态下,支持向量机模型和径向基函数网络模型都对测试样本进行了较准确的预测;从总体上看,支持向量机的回归值与测试值的吻合程度优于径向基函数网络.2种模型的误差比较示于表1.从表1可以看出,支持向量机模型的平均误差小于1%,远小于径向基函数网络模型;尤其在冷态启动和温态启动下,支持向量机模型的平均相对误差仅是径向基网络模型的1/4,说明在汽轮机转子应力变化剧烈的情况下,支持向量机模型具有更好的泛化性及稳定性.

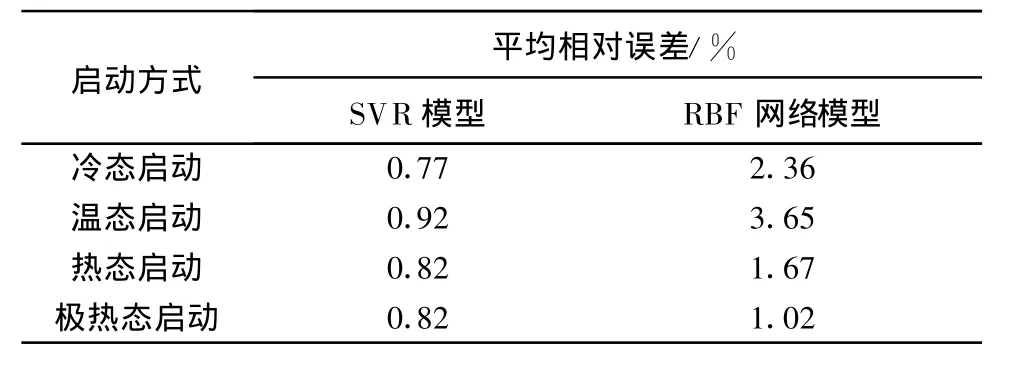
表1 SVR模型与RBF模型相对误差的比较Tab.1 Relative error comparison between SVR and RBF

4 结 论

通过对汽轮机转子应力计算的分析,采用支持向量回归算法对转子的应力修正系数进行建模,避免了应用一般神经网络进行回归分析过程中容易遇到的网络结构选择问题及局部极小等问题.对测试数据进行验证,结果表明:与一般的神经网络相比,在样本数据有限及目标数据影响因素复杂的情况下,该模型可以更准确地对转子应力的修正系数进行预测,而且模型的稳定性更好,泛化能力更强,能够满足对汽轮机转子应力在线监测的要求,为机组运行人员及时准确地了解转子应力的变化提供有效手段.

[1]丁有宇,周宏利,徐涛,等.汽轮机强度计算[M].北京:水利电力出版社,1985.

[2]吴志锋,周宇阳,陈汉平.600 MW汽轮机空气强制冷却时高中压转子热应力比较[J].上海汽轮机,2000(4):8-13.

[3]陈四利,杨凤,金生吉,等.汽轮机转子温度场和应力场的有限元分析[J].沈阳工业大学学报,2007,29(2):125-129.

[4]张恒良,谢诞梅,熊杨桓,等.600 MW汽轮机转子高精度热应力在线监测模型研制[J].中国电机工程学报,2006,26(1):21-25.

[5]武新华,宋春汀,张新江,等.汽轮机转子热应力简化计算公式的选取[J].汽轮机技术,2000,42(1):20-23.

[6]吕智强,韩万金.采用热流法计算汽轮机转子表面热应力[J].动力工程,2005,25(6):765-769.

[7]SHI Jinyuan,YANG Yu,DENG Zhicheng,et al.A neural network based method for on-line calculation of equivalent stress in steam turbine rotors[C]//International Conference on Power Engineering.Hangzhou:Chinese Society of Power Engineering,2007.

[8]HAYKIN Simon.神经网络原理[M].叶世伟,史忠植,译.2版.北京:机械工业出版社,2004.

[9]侯媛彬,杜京义,汪梅.神经网络[M].西安:西安电子科技大学出版社,2007.