高速透平膨胀机叶轮动力学模态的有限元分析

李 超, 艾丽昆, 刘延峰, 顾文婷

(兰州理工大学石油化工学院,兰州730050)

透平膨胀机是利用气体膨胀输出外功并产生冷量的机器.它是空气分离设备、天然气(石油气)液化分离设备和低温粉碎设备等获取冷量所必需的重要部件,是保证整套设备稳定运行的关键部分.透平膨胀机的核心部件是叶轮.在实际工作中,叶轮结构受到随时间变化的动载荷作用,如由于叶轮入口气流分布的不均匀及转子的不平衡产生的离心力等周期性载荷的作用[1-2].当其所受的动载荷较大时,或者虽然动载荷不大,但作用力的频率与叶轮的某一阶固有频率相等或接近时,叶轮会产生强烈的共振,从而造成很高的动应力,导致叶轮结构强度破坏或变形[3-5].因此,叶轮振动特性分析对于保证机器的稳定和安全运行十分重要.笔者对透平膨胀机叶轮进行了预应力下的模态分析,对提高机器运行的可靠性、安全性以及延长透平膨胀机的使用寿命均具有理论意义和实际意义.

1 叶轮结构的动力方程[6-7]

根据振动学理论,具有多自由度结构系统的动力方程可表示为:

{Q}节点载荷列阵通常是时间的函数.对于不同的结构,可以选用不同的单元和形状函数矩阵,但动力方程的建立过程均相同.在模态分析过程中,可以研究分析叶轮在无激振力作用下的自然属性.因此,取{Q}={0},则动力方程简化为:

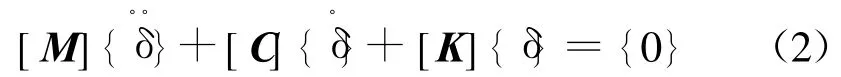
由于结构阻尼较小,对固有频率和振型的影响可忽略不计,由此可得到叶轮结构无阻尼自由振动方程:

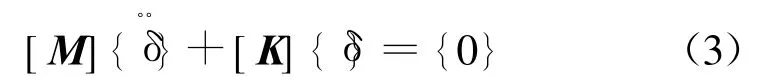
弹性结构的振动本身是连续体的振动,位移是连续的,具有无限多个自由度.经有限元离散化后,单元内的位移按假定的位移形式进行变动,并可用节点位移插值表示.这样,连续系统的运动可离散化为有限个自由度系统的运动.如全部节点有N个自由度,则式(3)即为N阶自由度系统的自由振动微分方程.

当透平膨胀机叶轮高速旋转运动时,受离心力作用而产生径向拉应力.在进行叶轮模态分析中这一载荷被作为初应力处理.因此,方程中[K]刚度矩阵主要考虑了初应力刚度矩阵[Kg]和弹性刚度矩阵[Ke],而初应力刚度矩阵[Kg]则来源于叶轮内部的初应力.初应力刚度矩阵考虑了初应变所产生的非线性刚度矩阵.在叶轮的旋转平衡位置附近和叶轮小变形范围内,可以认为初应变产生的非线性不显著,应力不受应变二次项的影响,因而可忽略大变形对平衡方程的影响.因此,将求解叶轮微幅振动平衡位置简化为叶轮在静力分析条件下得到的离心拉应力作用在叶轮上的各个离散有限单元.根据非线性有限元理论,某一个单元的初应力刚度矩阵Kgi表示为:

式中:N1～N4 分别为节点插值形函数;σx、σy、σz分别为初应力分量;dV为体积微元.

弹性刚度矩阵表示为:

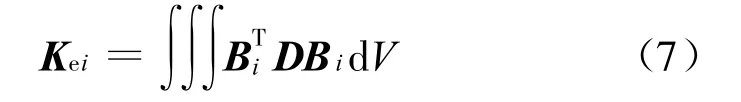
式中:Bi为单元应变矩阵;D为弹性矩阵.

2 基于预应力下的叶轮模态分析

由于叶轮的结构特点,叶轮在高速旋转过程中的旋转刚化作用对模态分析具有明显的影响.因此,本文采用考虑叶轮离心力影响的预应力分析模型.一般,基于Ansys的高速透平膨胀机叶轮动力学模态分析包括:①建立叶轮实体模型;②叶轮前处理;③划分网格后添加约束条件,对模型进行静力分析;④叶轮带有预应力下的模态分析;⑤计算结果后处理,分析计算结果并得出结论[8].

2.1 叶轮的材料属性与建模

透平膨胀机的叶轮设计要求如下:叶轮材料为6A 02(旧牌号为LD2)锻铝合金,其密度为2 700 kg/m3;弹性模量为71 GPa;泊松比为0.31;叶轮工作转速为31 328 r/min.透平膨胀机的叶轮主要由轮盖、叶片和轮盘3部分组成.轮盖和轮盘的结构均为圆周对称结构,几何形状较简单,但叶片的几何形状较复杂,其前、后面均为一个空间的弯扭曲面.因此,叶轮的三维实体建模可通过Pro/E软件强大的曲面造型功能来实现.在建模过程中,考虑到有限元分析时对实际情况的模拟以及计算的准确性和可行性,对叶轮进行适当简化:①叶轮轮盘轮毂密封齿对叶轮整体的模态分析影响较小,在模型中可不考虑;②叶轮模型中可忽略各处的圆角与倒角;③叶轮中的焊接部位均作一体化链接处理.

2.2 叶轮模型的前处理、边界条件加载与后处理

将Pro/E建立的透平膨胀机叶轮实体模型导入Ansys后对其进行前处理:定义材料的弹性模量、泊松比和密度;采用20节点实体单元,自由网格划分方式(free mesh)对叶轮模型进行网格划分,并在关键部位采用modify mesh方式进行网格细化.划分网格完成后,对叶轮实体模型添加载荷和约束.模态分析中唯一有效的“载荷”是零位移约束.若指定了非零位移约束,程序将以零位移约束代替该约束;在叶轮的计算过程中,叶轮的载荷为离心力,约束为全自由度约束.首先,对叶轮实体模型进行静力计算,并在静力分析的基础上扩展模态,对模型进行带有预应力的模态分析,同时应用Block-Lanzos法求解振动方程的特征值.叶轮实体模型的静力计算完成后,观察结果并对其进行后处理.模态分析包括:①固有频率;②已扩展的振型;③相对应力和力的分布.

2.3 预应力下半开式叶轮的模态分析

划分网格后的半开式叶轮三维模型示于图1.在进行叶轮的振动频率和相应的模态计算分析时,由于高阶模态对振动系统的贡献不大,不会对系统产生较大的影响[8],因此,笔者只计算了半开式叶轮的前八阶模态,结果示于表1.图2和图3分别为典型的一阶和八阶振型图.

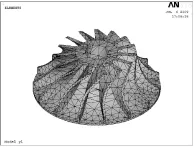
图1 划分网格后的半开式叶轮三维模型图Fig.1 Meshed three-dimensional model of semi-open impeller

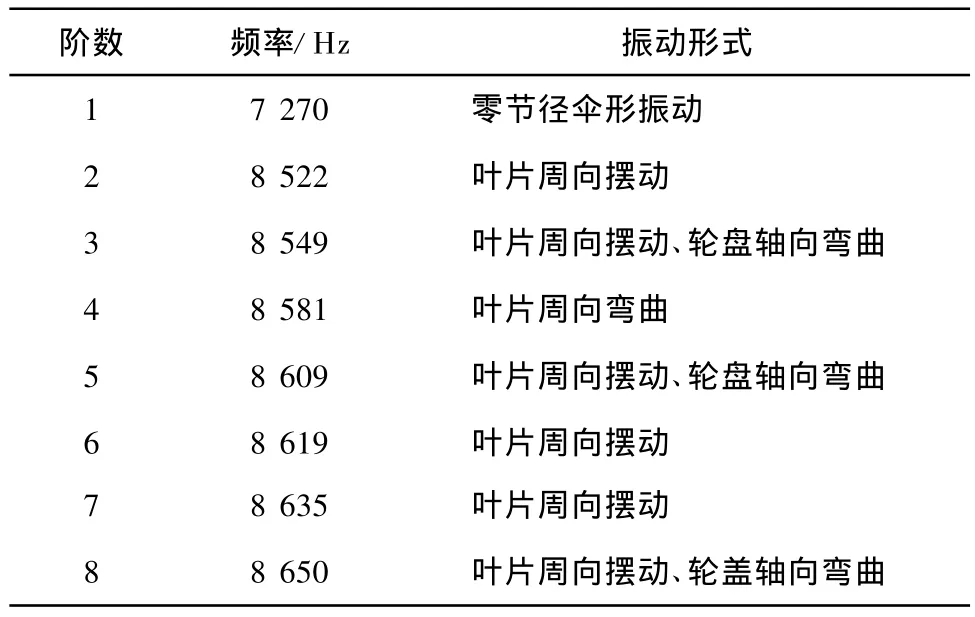
表1 半开式叶轮前八阶频率Tab.1 The first eight-order frequencies of semi-open impeller

图2 半开式叶轮一阶振型图Fig.2 The first-order vibration mode of semi-open impeller

图3 半开式叶轮八阶振型图Fig.3 T he eight-order vibration mode of semi-open impeller

2.4 预应力下闭式叶轮的模态分析

闭式叶轮的模态分析与半开式叶轮模态分析方法完全相同,其有限元网格划分示于图4.

图4 划分网格后闭式叶轮的三维模型Fig.4 Meshed three-dimensional model of closed impeller

通过相应的模态分析,由计算结果得到闭式叶轮的前八阶振动频率,结果示于表2,图5和图6分别为典型的一阶和八阶振型图.

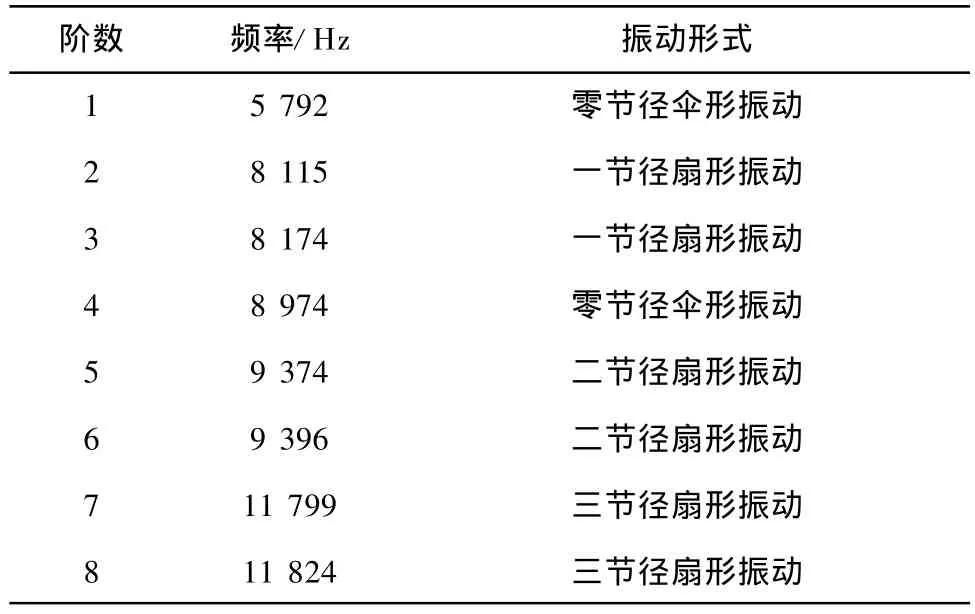
表2 闭式叶轮前八阶振动频率Tab.2 The first eight-order vibration frequencies of closed impeller

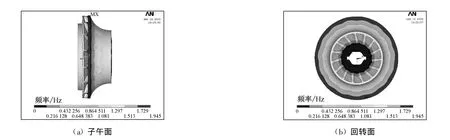
图5 闭式叶轮一阶振型图Fig.5 T he first-order vibration mode of closed impeller

图6 闭式叶轮八阶振型图Fig.6 The eight-order vibration mode of closed impeller

2.5 不同转速下闭式叶轮的模态分析

为深入分析离心力对叶轮的刚化作用和对模态分析的影响,笔者对不同转速下闭式叶轮的模态进行了分析,经计算得到闭式叶轮在不同转速下的固有频率和振型,其前八阶固有频率计算值示于表3.

3 分析与讨论

在进行模态分析时,半开式叶轮与闭式叶轮的模型结构尺寸完全相同,只是半开式叶轮比闭式叶轮少了轮盖部件,因此其质量低于闭式叶轮.通过对2种叶轮振型图的分析,可以看出:闭式叶轮低阶频率的振动形式以轴向摆动为主,此时,闭式叶轮的振动以质量效应为主,表现为低阶固有频率低于半开式叶轮;随着频率阶数的增加,闭式叶轮的振型变为轴向弯曲变形.由于离心力的刚化作用,使其固有频率有所加快,数值高于半开式叶轮(见表1和表2).

从2种叶轮的振型图可知:半开式叶轮由于叶片长厚比和宽厚比均较大,叶片比较薄,振动形式主要表现为叶片的周向摆动,叶片在内径处变形较大;而且半开式叶轮轮盘变形相对较小,主要表现为轴向的弯曲变形.闭式叶轮与半开式叶轮相比,增加了轮盖部件,轮盖对叶片的刚性具有增强作用,因此叶片的变形较小.由于叶片、轮盘和轮盖的振动耦合效应,闭式叶轮的变形以叶轮轴向摆动、弯曲以及扭转振动形式为主.随着叶轮振动频率的加快,叶轮的主要振型也在发生变化,由原来的零节径逐渐过渡到三节径,呈现出比较明显的扇形和伞形振动.确定模态频率是模态分析最基本的目的,因为确定了系统的模态频率就可以知道其在何频率范围内振动比较敏感;并且当外加激励频率与叶轮的固有频率一致时,会发生共振,同时叶轮振动幅度加剧,导致叶轮因共振而受到破坏.因此,在设计叶轮的旋转频率时,应避免共振区域,防止叶轮受破坏.图7所示的共振区域是应避免的危险区域.由表1和表2可知:透平膨胀机叶轮各部分的刚度较大,其频率也较快.半开式叶轮的第一阶频率(ω0=7 270 Hz)和闭式叶轮的第一阶频率(ω0=5 792 Hz)均远高于工作转速31 328 r/min时的频率(ω=3 279 Hz),即不在叶轮的共振区域范围内.由此可以确定:2种叶轮均能满足设计余量和振动安全性要求.所以,在一定的工作转速范围内选用叶轮时,可以不考虑叶轮产生共振的影响,只需直接根据叶轮的级比焓降和热效率等因素选取叶轮类型.通常,透平膨胀机的工作转速很高,大部分转速均在10 000 r/min以上,叶轮高速旋转产生的离心惯性力对叶片、轮盘以及轮盖的耦合振动特性具有显著影响.由于离心力的刚化效应,叶轮的固有频率比静频有所提高,且随着转速的提高,叶轮的振动频率也随之加快(表3).

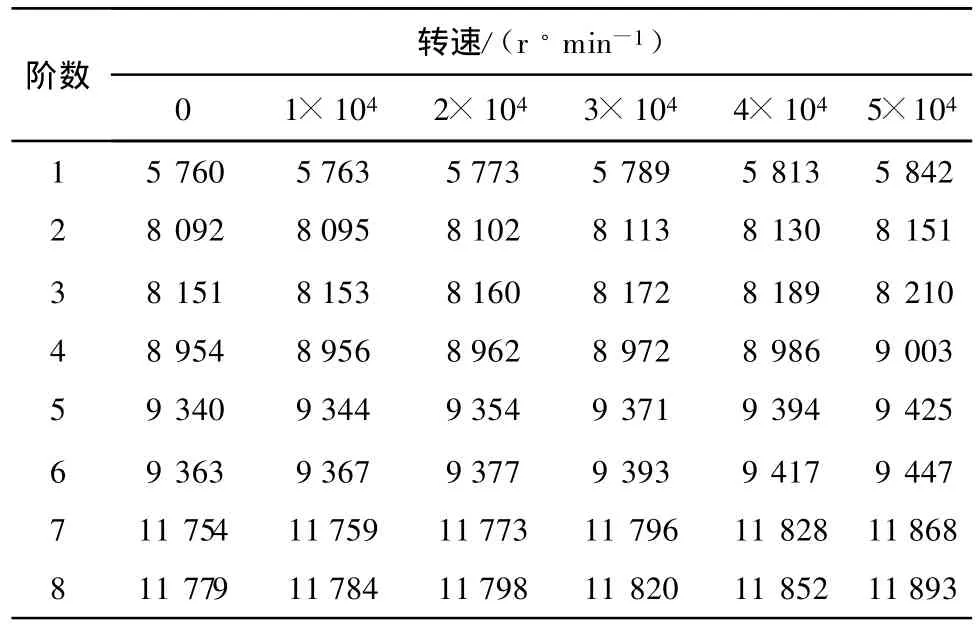
表3 闭式叶轮不同转速下的前八阶固有频率Tab.3 The first eight-order natural frequencies of closed impeller under different rotating speeds Hz

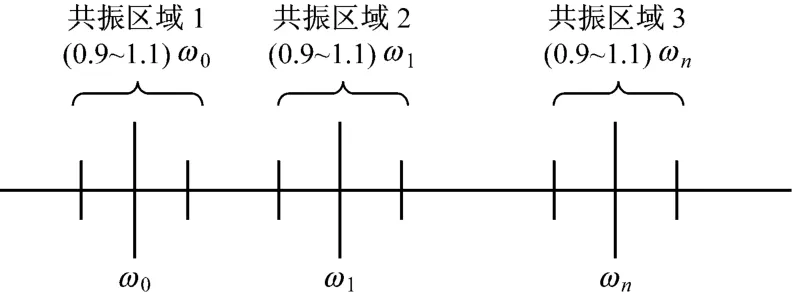
图7 叶轮的共振区域Fig.7 Resonance region of the impeller

4 结 论

(1)采用初应力模式将离心应力对固有频率的影响引入振动方程总刚度矩阵中,并对初应力刚度矩阵采用了小变形条件下计入非线性影响的线性处理,得到了叶轮在高转速下的固有频率.

(2)与闭式叶轮相比,半开式叶轮少了轮盖部件,轮盖对叶片具有刚性增强作用,因此半开式叶轮的频率和振动形式与闭式叶轮的完全不同.半开式叶轮的第一阶频率高且模态密集,振动形式以周向摆动和轴向弯曲为主;而闭式叶轮的频率与半开式叶轮的低阶相比较低且模态密度较小,振动形式以叶轮轴向摆动、弯曲和扭转振动形式为主;随着叶轮振动频率的加快,叶轮主要振型由原来的零节径逐渐过渡到三节径,呈现出较明显的扇形和伞形振动.

(3)叶轮的振动是轮盘、轮盖和叶片耦合的结果,由于其转动和变形的耦合将导致叶轮刚度增大,即使在小变形条件下,也将产生动力刚化现象.因此,动力刚化效应对叶轮固有频率的影响不可忽略.由于离心力的刚化作用,叶轮在不同旋转速度下的振动频率也不同,叶轮的固有频率比静频快,并且随着转速的提高,叶轮的振动频率也随之加快.

[1]张锦,刘晓平.叶轮机振动模态分析理论及数值方法[M].北京:国防工业出版社,2001:348-369.

[2]沈景凤,姚福生,王志远.微型燃气轮机向心透平的设计和研究[J].动力工程,2008,28(1):71-75.

[3]李德源,叶枝全,包能胜,等.风力机旋转风轮振动模态分析[J].太阳能学报,2004,25(1):72-77.

[4]张大义,陈璐璐,洪杰.离心叶轮与轴流叶轮振动特性的对比分析[J].战术导弹技术,2006(1):22-26.

[5]DIRK H,HEINRICH H,MANFRED R.Coupled vibratioin of unshrouded centrifugal compressor impellers[R].Germany:University of Hannover,2000.

[6]赵经文,王宏钰.结构有限元分析(第二版)[M].北京:科学出版社,2001:137-139.

[7]骆天舒,戴韧.整体式向心叶轮模态的有限元分析[J].内燃机工程,2005,26(1):77-80.

[8]杨阳,王益群,向小强,等.连体膨胀机叶轮应力及模态分析[J].流体传动与控制,2008,27(2):9-11.