1 MW塔式太阳能电站换热网络的动态模拟

李 显, 朱天宇, 徐小韵

(1.河海大学机电工程学院,常州213022;2.河海大学水利水电工程学院,南京210098)

符号说明:

T——温度,℃ρ——密度,kg/m3 d——直径,m Pr——普朗特数n——换热管数τ——时间,s D——壳径,m cp——比定压热容,J/(kg◦K)Re——雷诺数h——传热膜系数,W/(m2◦K)m——质量流量,kg/s λ——导热系数,W/(m◦K)Nu——努塞尔数μ——粘度,Pa◦s i——换热器分段数下标s——壳程流体t——管程流体o——外i— —内in——入口out——出口w — —管壁1——逆流程2——顺流程

塔式太阳能热发电系统集热温度高,是太阳能热利用的一个重要方向[1].目前,太阳能的间歇性是制约塔式太阳能热发电的重要因素之一,因此蓄热系统是塔式太阳能热发电系统的重要组成部分.换热网络作为蓄热系统和集热系统的桥梁,起着传递热能的重要作用.在蓄热系统充、放热时,换热网络的工作状况直接影响蓄热系统的正常运行.

在塔式太阳能热发电系统中,由于换热网络在运行时受到入口温度和流量的扰动,采用流量进行精确控制尤为重要.因此,建立换热器的动态数学模型并进行换热网络动态特性研究是塔式太阳能电站蓄热系统实时控制的前提.国内外学者针对管壳式换热器的动态特性进行了大量研究.Roppo等[2]和Correa等[3]采用有限元法研究了多管程换热器的动态特性;Roetzel等[4]建立了单壳程、多管程换热器的数学模型,并采用拉氏变换研究了换热器入口温度扰动对出口温度的动态影响,但此模型未能反映流量扰动对出口温度的动态影响;Luo等[5]利用拉氏变换建立了多管程换热器的动态数学模型,并对简单换热器网络的动态特性进行了分析,但此模型不能反映入口温度和流量同时扰动时换热器的动态特性;吴峰等[6]建立了管壳式换热器的动态模型,并采用顺、逆流换热器串联的方式进行了换热器的动态特性预测.

在上述研究的基础上,笔者建立了管壳式换热器的分布参数模型,并采用非线性机理模型对 1 MW塔式太阳能电站蓄热系统中换热器A和C的动态特性进行了计算.

1 塔式太阳能电站蓄热系统

1 MW塔式太阳能电站蓄热系统采用双级蓄热流程结构,将太阳能集热器吸收到的热量根据品位进行分级存贮,具体热力流程示于图1.

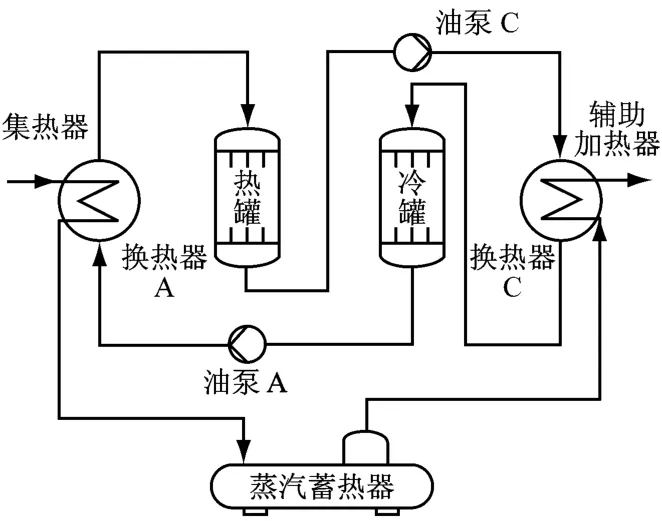
图1 蓄热系统示意图Fig.1 Schematic of thermal storage sy stem

1.1 充热

太阳能集热器产生压力为2.5 MPa、温度为400℃、流量为8.4 t/h的过热蒸汽,其中一路过热蒸汽进入高温蓄热系统的换热器A,在加热蓄热工质(导热油)的同时将大部分高温显热(261.4～400℃)存储于热罐中;另一路过热蒸汽经过降温降压(压力变为2.43 MPa)后,存储在低温蓄热系统(蒸汽蓄热器)中.

1.2 放热

当太阳能不足时,存储于蓄热系统的热能可以释放出来,产生蒸汽供汽轮机使用,具体方法如下:蒸汽蓄热器经过节流装置产生流量为8.4 t/h、压力为2.35 MPa、温度为220.7℃的饱和蒸汽;饱和蒸汽进入换热器C,被来自热罐的350℃高温导热油加热到320℃;之后这部分蒸汽在辅助加热器中进一步被加热到汽轮机要求的入口温度,然后进入汽轮机作功;经换热器C降温后的240℃导热油先存储在冷罐中,冷罐中的导热油经过换热器A加热后再存储于热罐中.

2 数学模型

2.1 换热器A和C的组成

换热器A和C均由4台同类型的1-2型管壳式换热器逆流串联组成,管程流体为蒸汽,壳程流体为高温导热油.换热器的网络结构示于图2.

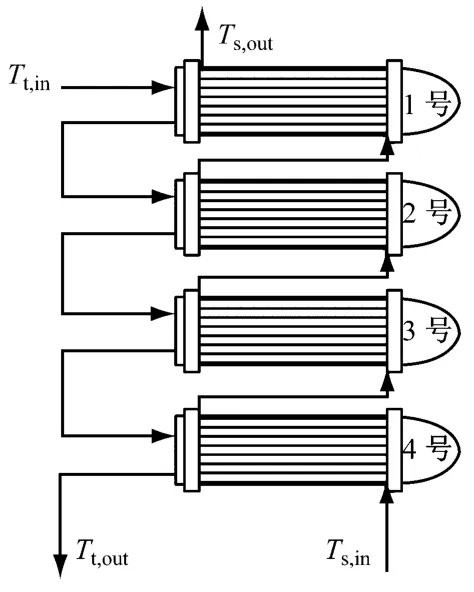
图2 换热器网络结构图Fig.2 Structure drawing of heat exchanger networks

2.2 动态数学模型

管壳式换热器的非稳态数学模型是对时间和空间的偏微分方程组.首先对管壳式换热器的实际模型进行简化,提出如下假设[7-8]:

(1)沿流体轴向流动方向的传热及壳体散热损失忽略不计;

(2)流体为不可压缩流体,无相变;

(3)流体及换热管的热物理性质为常数;

(4)冷热流体的流动为平推流状态,冷热流体没有轴向混合,属于分布参数模型.

为了求解分布参数模型,将换热器沿轴向方向划分为一些长度为dx的微元(图3),有效换热段总长为L.根据上述假设,建立了1-2型管壳式换热器的动态数学模型:

图3 管壳式换热器示意图Fig.3 Schematic of shell-and-tube heat exchanger

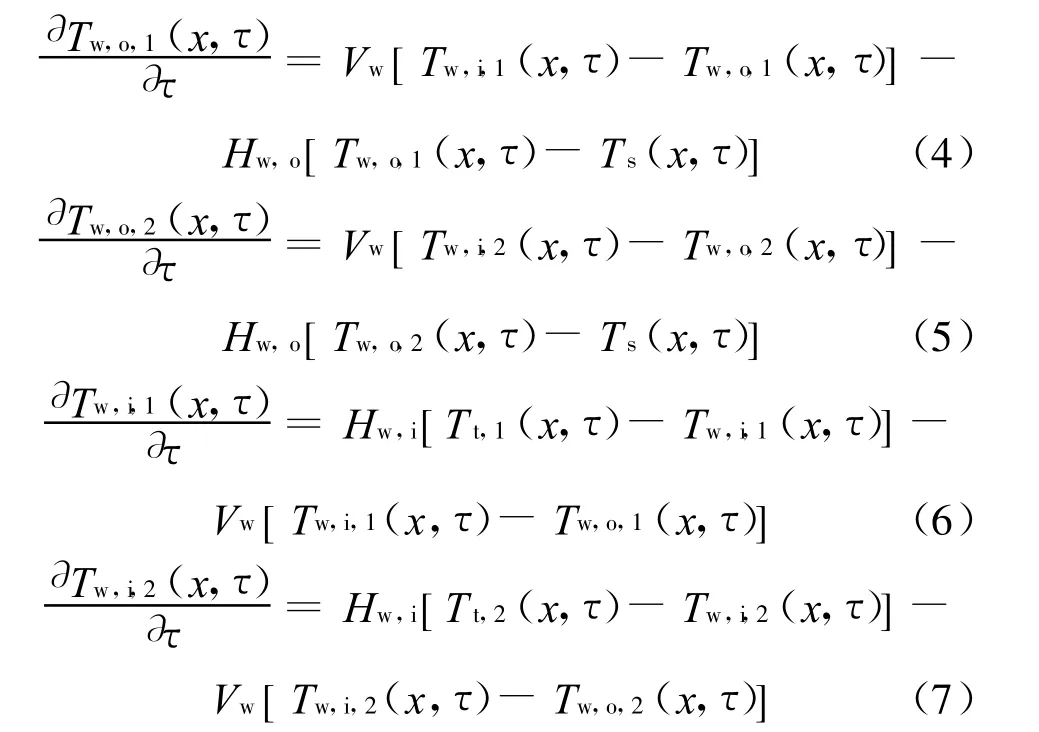
边值条件如下:Tt,1(0,τ)=Tt,1,in;Tt,2(0,τ)=Tt,2,out;Ts(L,τ)=Ts,in;Ts(0,τ)=Ts,out;Tt,1,out=Tt,2,in.

管内传热系数采用Sieder-Tate公式[9]:

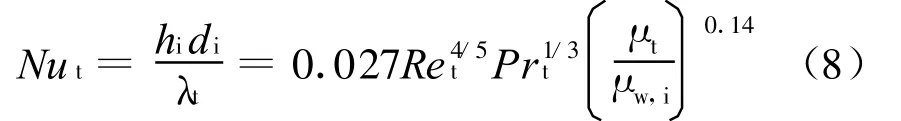
管外传热系数的计算公式为[9]:

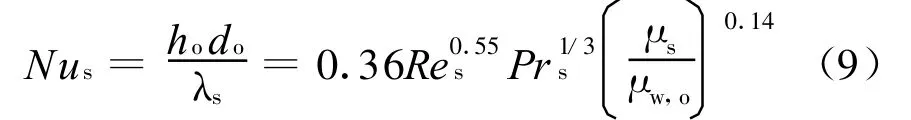
2.3 数值计算方法

对式(1)～式(7)进行分段集中化处理,将换热器沿x方向进行空间离散化,可得到换热器的非线性机理模型:

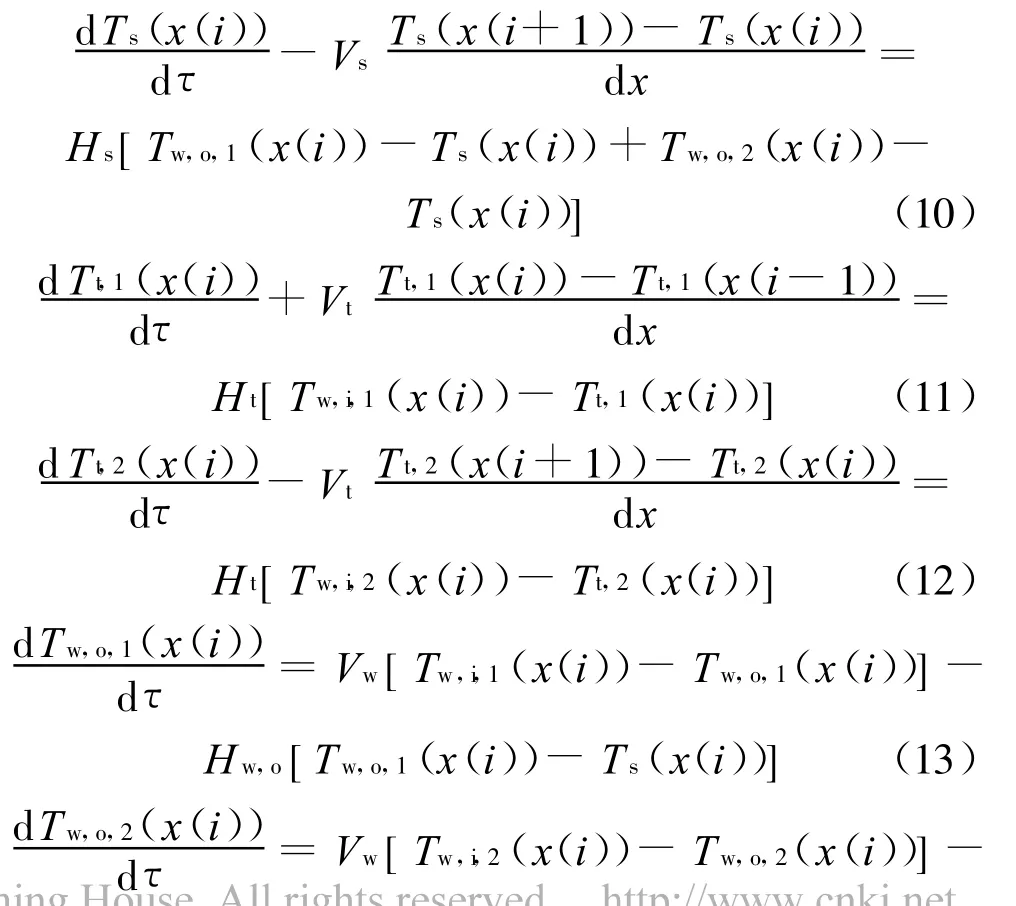
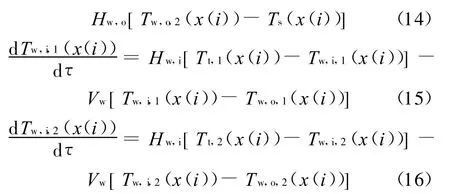
2.4 模型的验证

采用非线性模型对1个1-2型管壳式换热器的动态特性进行了模拟计算,模拟初始条件见文献[10].图4为管程流体流量发生阶跃变化时,换热器管、壳程流体出口温度的动态响应图.由图4可知,本文模拟值与文献计算值的偏差在扰动初始时刻相对较大,这是因为文献计算值采用了线性化模型,而本文采用的是非线性机理模型.图4中模拟值与计算值吻合良好,证明本文的换热器计算模型具有较好的准确性.

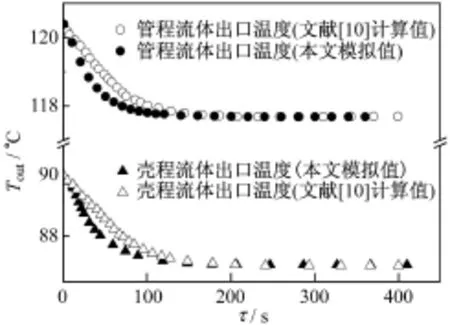
图4 换热器A出口温度模拟值与计算值的比较Fig.4 Comparison between the simulated results and the calculated results of the outlet temperature of heat exchanger A

2.5 换热网络模拟方法

由于动态模拟以定物性为假设条件,为减小计算误差,可采用模块化仿真方法,即将单台1-2型换热器作为一个模块,每个模块具有独立的物性参数.根据换热器A和C的网络结构进行动态特性计算.

3 模拟结果与分析

3.1 模拟条件

换热器A和C中1-2型管壳式换热器的几何参数为:D=0.6 m;L=3 m;n=283;d0=0.025 m;di=0.02 m.

换热器A:Ts,in=240℃;Tt,in=400℃;ms=2.735 kg/s;mt=2.333 kg/s.

换热器C:Ts,in=350℃;Tt,in=220.7℃;ms=2.75 kg/s;mt=2.333 kg/s.

导热油采用Therminol VP-1.

3.2 换热器A的动态特性

在蓄热系统充热时,换热器A易受集热器出口过热蒸汽温度、流量及温度和流量同时扰动的影响.图5、图6、图7分别为过热蒸汽温度、流量以及温度和流量同时扰动下,换热器A两侧流体出口温度的动态特性图.由图5～图7可知,当集热器出口过热蒸汽温度、流量或温度和流量同时在第10 min和第60 min发生阶越扰动时,导热油和过热蒸汽出口温度的动态响应时间一致,约为30 min.

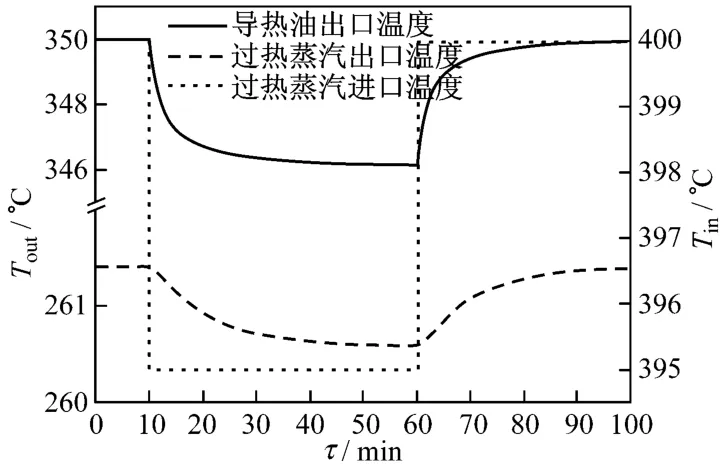
图5 在过热蒸汽温度扰动下,换热器A出口温度动态特性Fig.5 Dynamic behaviour of outlet temperature of heat exchanger A under the disturbance of superheated steam temperature

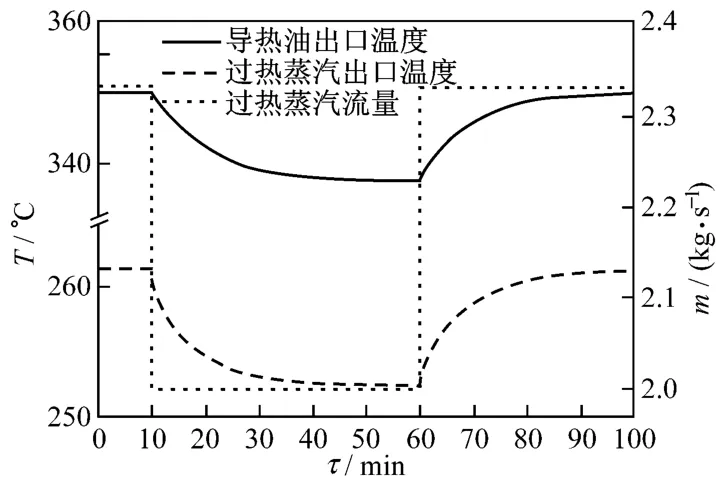
图6 在过热蒸汽流量扰动下,换热器A出口温度动态特性Fig.6 Dynamic behaviour of outlet temperature of heat exchanger A under the disturbance of superheated steam flow rate

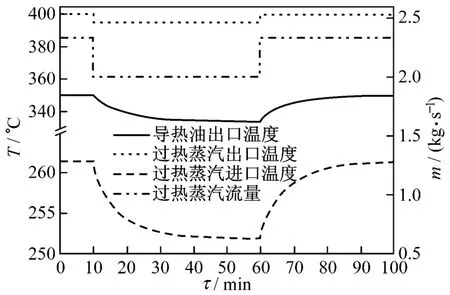
图7 在过热蒸汽温度和流量同时扰动下,换热器A出口温度动态特性Fig.7 Dynamic behaviour of outlet temperature of heat exchanger A under the disturbances of superheated steam temperature and flow rate

3.3 换热器C的动态特性

在蓄热系统放热时,蒸汽蓄热器出口蒸汽维持饱和状态,随着出口饱和蒸汽压力的下降,温度也随之降低.图8为蓄热器出口蒸汽温度阶跃下降时,换热器C两侧流体出口温度的动态特性图.由图8可知,导热油和蒸汽出口温度的动态响应时间基本一致,约为20 min.

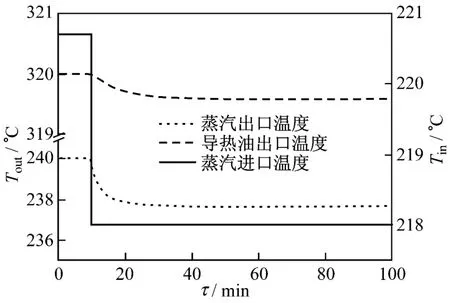
图8 在蒸汽进口温度扰动下,换热器C出口温度动态特性Fig.8 Dynamic behaviour of outlet temperature of heat exchanger C under the disturbance of inlet steam temperature

当蓄热系统在充、放热同时进行的模式下运行时,换热器C导热油侧进口温度必然发生扰动,此时换热器C出口温度的动态特性示于图9.由图9可知,当热罐出口导热油温度在第10 min和第60 min发生阶越下降和上升时,换热器C蒸汽侧出口温度响应没有时滞,但受换热器C网络结构的影响,导热油侧出口温度有5 min左右的响应时滞,其动态响应时间与蒸汽一致,约为20 min.

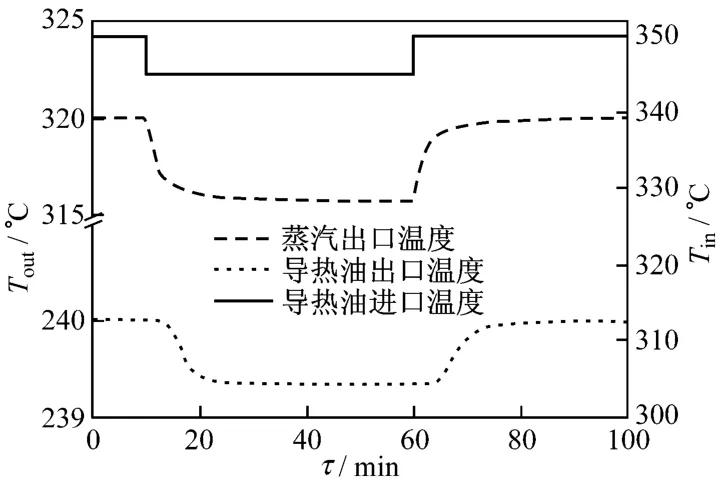
图9 在导热油进口温度扰动下,换热器C出口温度动态特性Fig.9 Dynamic behaviour of outlet temperature of heat exchanger C under the disturbance of inlet temperature of heat transfer oil

4 结 论

(1)换热器A和C都具有较大的热惯性,其动态响应时间分别为30 min和20 min.

(2)在过热蒸汽温度、流量以及温度和流量同时扰动下,换热器A蒸汽和导热油的出口温度响应无时滞.

(3)在蒸汽进口温度的扰动下,换热器C蒸汽和导热油的出口温度响应无时滞;而在导热油进口温度的扰动下,换热器C的导热油出口温度存在响应时滞.

[1]ROMERO M,MA RCOS M J,TELLEZ F M,et al.Distributed power from solar tower systems:a mius approach[J].Solar Energy,1999,67(4/5/6):249-264.

[2]ROPPO M N,GANIC E N.Time-dependent heat exchanger modeling[J].Heat Transfer Engineering,1983,4(2):42-46.

[3]CORREA D J,MARCHET TI J L.Dynamic simulation of shell-and-tube heat exchangers[J].Heat Transfer Engineering,1987,8(1):50-59.

[4]ROETZEL W,XUAN Y.T ransient behaviour of multipass shell-and-tube heat exchangers[J].International Journal of Heat and Mass Transfer,1992,35(3):703-710.

[5]LUO Xing,GUAN Xin,LI Mei-ling,et al.Dynamic behaviour of one-dimensional flow multistream heat exchangers and their networks[J].International Journal of Heat and Mass Transfer,2003,46(4):705-715.

[6]吴峰,曾敏,吴一宁,等.连续螺旋折流板换热器动态特性的数值预测和分析[J].动力工程,2007,27(4):573-578.

[7]孙宝芝,曹民侠,赵嘉明,等.管壳式换热器瞬态换热性能分析[J].哈尔滨工程大学学报,2007,28(12):1332-1336.

[8]解增忠,张俊峰,罗雄麟,等.管壳换热器模型库及在换热网络仿真中的应用[J].系统仿真学报,2005,17(12):2882-2887.

[10]罗雄麟.化工过程动态学[M].北京:化学工业出版社,2005:52-53.