电机的定点DSP控制中转速测量新方法

赵仁德,曲华龙

(1.中国石油大学(华东)信息与控制学院,山东 东营 257061;2.山东省荣成市华力集团,山东 威海 264300)

1 引言

定点DSP具有成本较低、对存储器的要求较低、耗电少及丰富的专用接口等优点,在现代电机控制系统中得到广泛应用[1]。随着电机调速精度要求越来越高,调速范围越来越大,如何在较大的转速范围内快速准确地检测转速,是电机控制系统需要解决的关键问题之一。光电编码器和DSP性能的提高为高精度转速检测奠定了基础。但在电机调速系统中,DSP是控制系统的核心,测速只是DSP的一部分任务,不宜过多地占用DSP的硬件和软件资源。传统的M 法、T法及M/T法不能适应基于定点DSP的电机数字控制的需要。

本文以Ti公司的 TMS320F2812 DSP为例分析了上述3种传统测速方法存在的问题,提出了一种适合于定点DSP测速的最大绝对和相对误差可控的测速方法,并进行了实验验证。

2 增量式光电编码器与QEP电路

一般来说增量式光电编码器有3路信号输出:A,B和Z。A,B信号正交,相位差90°,超前滞后关系取决于光电编码器的转向。Z信号是光电编码器每转一圈输出的那一个脉冲信号。

光电编码器输出的A,B,Z信号通过光耦隔离、电平转换和整形接到DSP的QEP引脚上[2]。在TMS320F2812中,有2个QEP单元,可以将A,B和Z信号分别接到CAP1-QEP1,CAP2-QEP2和CAP3-QEPI1(或CAP4-QEP3,CAP5-QEP4和CAP6-QEPI2)引脚上。经过 QEP电路,不仅可以得到4倍于A,B信号的脉冲信号QEP-CLK,而且还可以得到电机的转向信号DIR,如图1所示,这都是DSP内部电路完成的功能。

图1 QEP电路的输入和输出信号Fig.1 Input and output signals of the QEP circuit

3 传统测速方法存在的问题

通用定时器2(或通用定时器4)对QEPCLK进行计数,得到以脉冲个数表示的转子角度信息,即转子位置角。需要注意的是,这个角度是相对于Z信号出现的位置而言的,是增量角度。

某段时间ΔT内转子位置角的变化量 Δ θ除以这一段时间,即得到转速[3]:

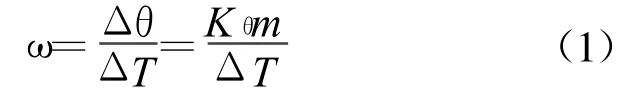
式中:m为在这段时间内QEP-CLK的脉冲数;Kθ为每个脉冲对应的机械角度。

T法测速测量的是转子转过确定的Δ θ角所经历的时间ΔT,然后根据式(1)计算转速。它不适用于定点DSP的测速,主要原因有2点。

1)ΔT是变化的,在计算转速时必须采用除法,Ti C2000系列定点DSP中没有除法指令,需调用虚拟浮点数学库(IQmath.lib)中的除法函数[4],调用一次需要63个指令周期,而执行一次16位乘法只需1个指令周期,所以计算量较大,计算时间较长。

2)QEP电路得到的脉冲信号不是DSP的中断源,而且Ti C2000定点DSP的中断无法嵌套,无法准确得到ΔT。

M法测速测量的是在确定的时间段ΔT内,转子转过的角度 Δ θ,然后根据式(1)计算转速。其优点是可用乘以1/ΔT取代除以ΔT,以节省DSP运算时间。其不足是低速测量误差较大,如需减少误差,则要增加测速时间,这将影响高速下的动态响应。

可见,传统的M法和T法测速均不适用于转速变化较大的场合。M/T法测速[5]可在高速和低速下均能准确测速。其基本思想是将M法和T法相结合,在确定的时间ΔT内,测得m个脉冲,第m+1个脉冲不完整,则对这个脉冲的不完整部分进行计时为ΔT′,则转速为

由式(2)可知,分母不是确定的,所以M/T法测速也不适合于定点DSP的测速,原因同T法测速一样。

4 适合于定点DSP的测速方法

由上面的分析可知,T法和M/T法测速不适合于定点DSP测速。而传统的M法测速则不能满足在较大转速范围内高精度测速的需要,需对其进行改进。

在确定的ΔT的时间内,M法测速最多可能少计或多计2个脉冲。测速的最大绝对误差为

所以,M法测速的绝对误差取决于2个因素:一是光电编码器的线数,线数越多,Kθ越小,误差越小;二是测速的时间间隔ΔT,ΔT越小,误差越大。M法测速的最大绝对误差与转速的高低无关。提高光电编码器的线数和增大ΔT,可减少绝对误差。

设在ΔT时间内,计数器计得的脉冲数为m,则测速的最大相对误差为转速越高,m越大,最大相对误差越小;反之,转速越低,m越小,最大相对误差越大。提高光电编码器的线数和增大 ΔT,可以增大m,可减少相对误差。

可见,在使用相同的光电编码器的情况下,增大ΔT是提高测速精度的唯一方法。但增大ΔT必将影响动态响应。传统的M法测速,因为ΔT是确定的,不能兼顾动态响应与测速精度,所以不适合转速变化较大的场合,必须进行改进。本文提出了一种适合于定点DSP测速的新方法。

首先通过设定最短时间ΔTmin来限制绝对误差。在ΔTmin内不读取m的数值,也不进行转速计算。其次通过设定脉冲数的下限值mmin来限制相对误差。当脉冲数小于mmin,不进行转速计算。通过这2个条件来限制最大绝对和相对误差。

若在ΔTmin内,脉冲数已超过了设定的下限值mmin,则进行转速计算。如在 ΔTmin内,脉冲数小于设定的下限值mmin时,则延长计数时间为原来的2倍,如仍不能满足,再增大计数时间2倍,依此类推,直至脉冲数大于mmin为止。此时计数的时间为

式中:n为延长计数时间的次数。这样转速的计算公式为

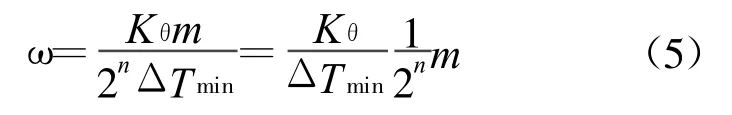
式中:m和n为变量;其它的量都是常数。

在定点DSP的运算中,除以2n可以用右移n位来实现,不使用除法,减少计算量。

5 实验结果

将所提出的测速方法用于以 TMS320F2812为控制核心的直驱式永磁同步风力发电系统的最大功率追踪控制中。在此系统中,发电机转矩指令由转速的结果进行运算得到[6],准确测速非常重要。采用型号为OIH60-TS5246的光电编码器,每转输出 8 192个脉冲,经 QEP电路 4倍频后得到32 768个脉冲。部分实验结果如图2和图3所示。

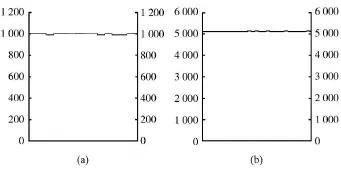
图2 不同转速下DSP测速结果Fig.2 Speed measurement results in DSP under different conditions

图2给出在不同转速下,从DSP中读出的格式为Q11的单位为r/s的测速结果。图2a所示的是发电机实际转速为29.086 r/min的测速结果,转换成以r/min为单位的实际值是1 000÷211×60=29.297 r/min;图 2b所示的是发电机实际转速为149.584 r/min的测速结果,转换成以r/min为单位的实际值是 5 118÷211×60=149.941 r/min。由此可见,DSP测速结果在不同的转速下都有较高的测速精度。

图3 风速突变时并网电流的动态响应Fig.3 Phase current response to step change in wind speed

图3给出了风速由6m/s突变为8 m/s然后再突变为6 m/s这一过程中 A相并网电流的波形。由图 3可以看出:风速为6 m/s时,并网电流的峰值约为5 A,风速为8 m/s时,并网电流约为12 A,在单位功率因数下,并网电流的幅值与系统向电网发出的功率成正比,所以,在2种风速下向电网发出的功率之比为12/5=2.4。而在最大功率点处,风力机的输出功率与风速的立方成正比[6],两种风速下风力机的输出功率之比为83÷63=2.37。考虑到风力机的输出功率与系统的并网功率之间有各种损耗,这表明系统有良好的最大功率追踪的动静态特性,也间接证明了测速方法的精确性。

[1]苏硅峰,吕强,耿庆锋,等.TMS320F2812原理与开发[M].北京:电子工业出版社,2005.

[2]谷海涛,颜湘武,曲伟.正交解码电路和捕获单元在转角和转速测量中的应用[J].电气应用,2005,24(1):113-115.

[3]陈伯时.电力拖动自动控制系统[M].第3版.北京:机械工业出版社,2003.

[4]付旭东,徐冰,薛必春,等.电动机转速的数字检测[J].控制工程,2003,10(2):186-189.

[5]Texas Instruments Inc..IQmath Library A Virtual Floating Point Engine[R].2002.

[6]赵仁德,王永军,张加胜.直驱式永磁同步风力发电系统最大功率追踪控制[J].中国电机工程学报,2009,29(27):106-111.