螺栓连接结构的爆炸冲击破坏*

金 晶,吴新跃

（海军工程大学机械工程系,湖北 武汉 430033）

现代海战中军舰受到精确制导武器攻击的概率越来越大。激光炸弹和反舰导弹等武器通常在舰体附近或舰体内部形成非接触爆炸,造成舰船结构及各种设备的破损,使舰船失去战斗力。在舰艇不沉没的情况下保持舰用设备的战斗力显得尤为重要,因此需要对舰用设备进行爆炸冲击响应分析。而各种设备的连接结构中应用最广泛的一种方式是螺栓连接,对设备的整体破坏分析必然涉及部件之间的连接,因此需要分析螺栓的冲击破坏响应,从而建立真实可信的螺栓连接破坏模型。

对结构抗爆的研究主要采用实验、理论分析与数值计算的方法。爆炸实验是检验结构抗爆性能最有效、最直接的方法,但破坏性实验耗资巨大[1]。爆炸冲击下,绝大部分重要部位的螺栓联接不只受轴向拉力的作用,而是受各个方向的力和力矩的作用,还受非周期性的瞬态作用以及考虑材料的塑性应变。这使问题成为状态非线性和材料非线性组合在一起的高度非线性问题,必须借助于有限元分析。

本文中建立3维螺栓有限元模型,采用部分降温法对螺栓施加预紧力,并用接触算法模拟螺栓和被连接件的相互作用。在此基础上对螺栓连接和螺栓-螺母连接分别进行不同情况的爆炸冲击分析,评估预应力大小对冲击响应的影响,建立螺栓连接的简化破坏模型。

1 求解方法理论分析

1.1 爆炸冲击波传播

用3维欧拉运动方程表达理想气体爆炸冲击波的传播[1]

式中:q为状态矢量,式（1）满足质量、动量、能量守恒定律,f（q）、g（q）、h（q）表示状态变量的流动

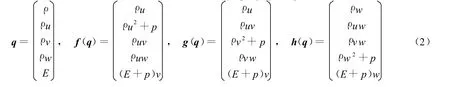
式中:ρ为材料密度;u,v,w为直角坐标系下3个速度分量;p为压力;E为气体总能量。

进行抗爆分析就是要找出在不同方向的爆炸冲击作用下结构的薄弱之处,并加以改进。本文中采用球面加载法对电站结构施加爆炸载荷,即将炸药起爆点布置在以结构为圆心的球面上。当球面半径为结构外形尺寸的10倍以上时,就能保证结构各部位的爆炸超压基本一致。当需要对不同距离上的爆炸进行评估时,先测出结构附近空气网格的冲击波峰值,然后利用下式[1]就能计算出不同距离上产生同样冲击波超压所需的炸药质量

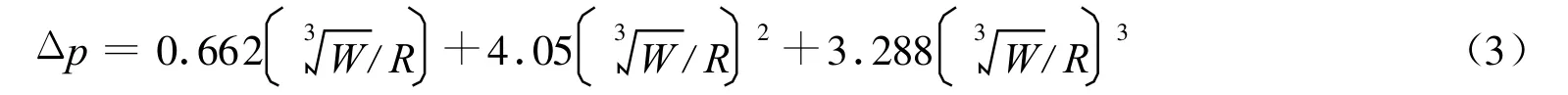
式中:R为爆炸点至测量点的距离,m;W为炸药质量,kg。

1.2 流固耦合算法

流固耦合算法是指在用有限元模拟爆炸作用时,通过一定的约束方法将结构与流体耦合在一起,以实现力学参量的传递。主要的约束方法有:速度约束、加速度约束和罚函数约束。这种算法的优点在于在进行有限元网格划分时,不需要耦合面上的流体单元和结构单元一一对应,大大减少了工作量。其中速度和加速度约束的计算步骤为:

（1）搜寻包含结构节点的流体单元,将结构单元节点参数（质量、动量、节点力）分配给流体单元节点

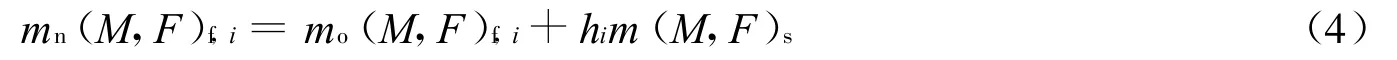
（2）计算新的流体节点加速度（速度）

（3）约束结构节点的加速度（速度）

式中:mn、mo分别为分配前后流体单元节点质量;M、F分别为动量、节点力;a、v为节点加速度和速度;h为单个流体单元中包含的节点数;f和s为流体和实体单元符号[2]。

1.3 接触算法

罚函数算法是ANSYS处理接-碰撞表面最常用的接触算法,相当于在2个接触面之间放置1个法向弹簧,使法向界面接触力的大小与穿透深度、主接触面刚度成正比。考虑2物体A、B接触问题,如图1所示,当前构形为 SA和SB,边界面为 ΩA和 ΩB,接触面记为ΩC=ΩA∩ΩB。由于2物体不能互相重叠,事先无法确定2物体在哪一点接触,因此只能在每一时步,对比 ΩC面上物体A、B的坐标或速率来实现位移协调条件[2]

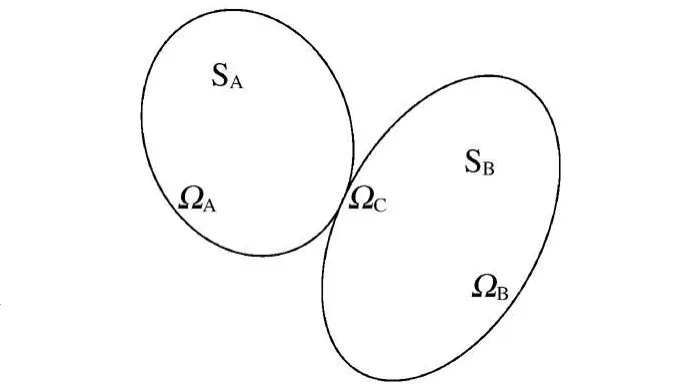
图1 接触算法原理图Fig.1 A principle for the contact algorithm

式中:U、V表示物体整体的位移和速度,u、v表示物体在接触点位移和速度,n表示接触界面法向矢量,N表示法线方向,由此产生表面接触和接触点间力的传递。

2 建立有限元计算模型

2.1 建立几何和有限元模型

螺纹部分的几何形状复杂,与螺母的接触面是1个空间螺旋面。螺纹升角很小,几何建模中忽略螺纹升角的影响,利用一系列标准螺牙代替连续螺纹。这样不仅将螺栓划分为计算精度更高的六面体网格,而且减少了网格数量。简化螺纹的螺栓有限元模型见图2。M24螺栓共划分六面体网格14 458个,节点16 491个;螺母划分网格3 130个,节点4 331个。

空气状态方程采用Gamma律状态方程,即

式中:p、ρ、e为气体的压力、密度、比内能,γ为气体比热比。计算中 ρ=1.2 kg/m3,e=250 J/g,γ=1.4。高速冲击下,材料的应力与应变关系随应变率的大小呈非线性变化。本文中采用应变率方程式[3]

2.2 预紧力的施加

现在普遍采用降温法对螺栓添加预紧力,即通过降低螺栓的温度来产生收缩变形,当这种变形受到被连接件的阻碍时,就会产生内部拉力,即预紧力Q0=αEAΔT[4],其中α为螺栓材料的线膨胀系数,E为螺栓材料的弹性模量,A为螺栓的危险截面面积,ΔT为温度变化量。

这种方法没有考虑螺纹间的应力分布,如果应用在此,就会造成螺栓两端的应变最大,导致底部螺纹应力大于2连接件的交界处的螺纹应力,在计算螺纹动态响应时就会与实际不符。本文中只对从螺栓顶部到螺纹受力最大的截面以上区域施加温度载荷。这样处理能够对螺纹高应力区只产生拉力,从而让拉应力自动在螺纹上合理分布[5]。

紧螺栓连接装配时需要拧紧,因此预紧螺栓截面除受拉应力外还受螺纹力矩T1所引起的扭切应力τ。由于本文中建立的有限元模型螺纹相互平行,没有螺纹升角λ,所以模拟拧紧力矩T1时,阻力全部由接触面间的摩擦力提供,等效摩擦因数f′=tan（λ+ρ′）可通过下式[6]计算

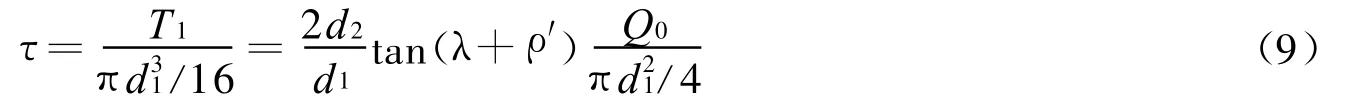
式中:d1、d2为螺纹小、中径,λ为螺纹升角,ρ′为当量摩擦角,τ≈0.5σ。施加轴向与拧紧力矩后,热膨胀因数取1.2×10-5。计算得到螺纹间应力分布如图3所示,从图中可以看出应力分布符合实际情况。

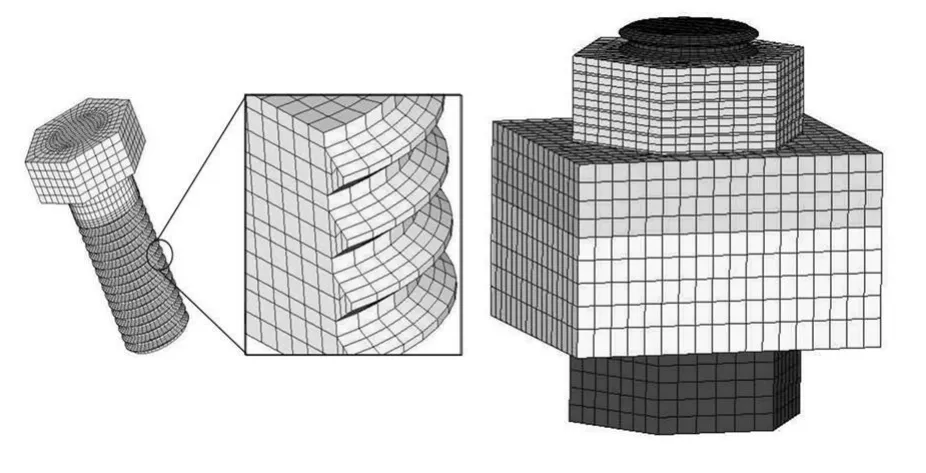
图2 螺栓连接有限元模型Fig.2 A finite element model of the bolt joint

图3 预紧螺栓剖面应力云图Fig.3 Prestress distribution on the bolt cross section

2.3 边界条件

建立包含所有实体单元的长方体空气网格,6个面全部作为冲击波加载面和非反射边界,即冲击波可以从任意位置传入和传出空气网格;在下部连接部件一侧施加固定约束,形成悬臂梁结构;流固耦合算法使用罚函数约束;接触算法使用面-面接触算法;仿真计算使用LS-DYNA进行,计算时间为1 ms。

3 M24螺栓仿真分析

3.1 螺栓自身受爆炸冲击响应

将爆炸点置于距离模型半径为1 m的球面上,对M24螺栓连接模型进行爆炸响应分析。由于螺栓螺母为轴对称,因此只需在xz平面上布点即可。螺栓连接在0°～90°上间隔45°布置3个点,螺栓-螺母连接在-90°～90°间隔45°布置5个点。分别计算有、无预应力时的响应情况。图4为2种连接方式各方位爆炸条件下受力最大的单元应力时程曲线。从图中可以看出,在螺栓连接情况下,在有、无预应力时45°方向爆炸单元均已达到塑性变形;有预应力时0°方向上最大应力约800 MPa;其余3种情况应力峰值值较小,峰值约400 MPa。对螺栓-螺母连接,有、无预应力时-45°、0°、45°方向单元达到塑性应变;90°方向应力峰值最小,有预应力时的应力峰值大于无预应力时的应力峰值但差距不大;-90°方向有、无预应力时应力峰值均约840 MPa。

将上述计算结果中达到塑性应变的单元做一个塑性应变率的比较,各种情况的最大塑性应变如表1所示。从表中可以看出,在所有达到塑性应变的单元中,螺栓-螺母联接的-45°方向对螺栓冲击最大,其中无应力情况下单元已经达到极限应变而失效,其次是螺栓联接45°方向,其余方向应变较小。

表1 各种情况下单元的最大塑性应变Table 1 Maximum plastic strain of elements under different conditions

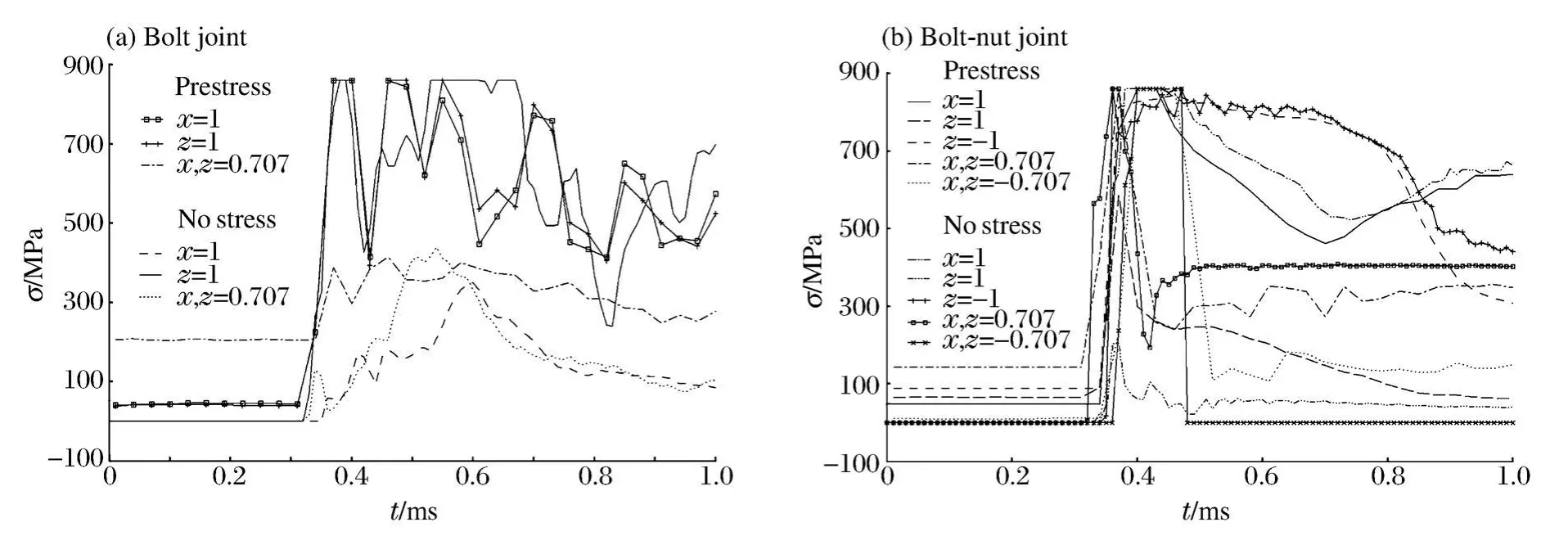
图4 各种爆炸情况下单元的最大应力曲线Fig.4 Maximum stress-time curves of elements under different explosion conditions

综上所述,爆炸冲击对螺栓自身作用时,斜向入射时对连接螺栓的冲击作用最大;螺栓-螺母连接受冲击时,内部应力明显大于螺栓连接,特别是有螺母的那端首先受到爆炸冲击时,峰值应力明显较高;而预紧应力对冲击效果的影响不明显。

3.2 螺纹连接部件爆炸冲击响应

机械系统受爆炸冲击时,除螺栓连接本身受冲击波作用外,连接的部件也受冲击波的作用,所受作用力还会传递到螺栓连接处对螺栓连接产生作用。由此产生的破坏远大于冲击波对螺栓自身的作用。因此在分析螺栓自身的基础上必须分析连接部件受爆炸冲击的响应情况。连接件冲击波作用面积与螺栓破坏形式密切相关,无法对所有情况做出分析,因此只分析冲击波入射角度与螺栓破坏冲击力大小的关系。受计算机条件限制,无法将包含有螺栓详细模型的机构整体进行流固耦合计算,因此采取施加等效爆炸

载荷的方法进行分析。在空气中传播时,爆炸冲击波超压值呈指数函数变化[7]

式中:Δp0为冲击波超压初始值,τ+为冲击波作用时间,b为常数。因此连接件上的压力也呈指数变化。在由式（10）所得的曲线上均匀取10个点作为压力载荷施加在连接件的冲击波作用面上见图5。

首先对螺栓连接预紧力从0～300 MPa间隔50 MPa取值,冲击载荷施加在0°、45°和90°等3个方向进行冲击破坏计算,为了保证螺栓被破坏而不是被连接件被破坏,此处被连接件材料屈服应力取值远高于螺栓材料,计算结果见图6。从图中可以看出,无论是哪个方向的冲击,连接预紧力对螺栓破坏的临界值影响很小,约5%。这说明正常的螺栓预紧力产生的摩擦力和阻力与冲击力相比很小,不影响冲击破坏效果,因此可以忽略预紧力的影响。

图5 在螺栓联接件上施加载荷Fig.5 Adding load on a bolt joint part

其次分析冲击波入射方向对螺栓破坏的影响。文中分析的是螺栓连接破坏的临界值,与图示相反方向的作用力会部分作用在下连接件上,计算结果肯定要大,因此冲击波入射角只在0～90°间取值,方向见图5。分别计算螺栓和螺栓-螺母连接破坏临界值,结果见图7。从图中可以看出,2条曲线形状相似,最大值出现在约25°,最小值出现在约70°。但是螺栓-螺母联接的0°方向值要大于90°方向,而螺栓联接则0°方向小于90°方向。总体来看,螺栓-螺母连接的抗冲击破坏能力大于螺栓连接的。

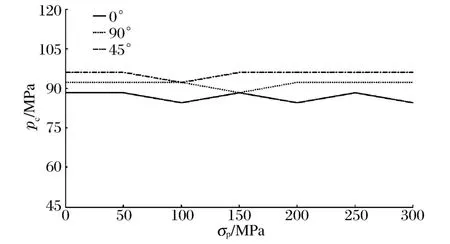
图6 预紧力对临界破坏载荷的影响Fig.6 Critical damage load affected by prestress

4 螺栓简化破坏模型建立

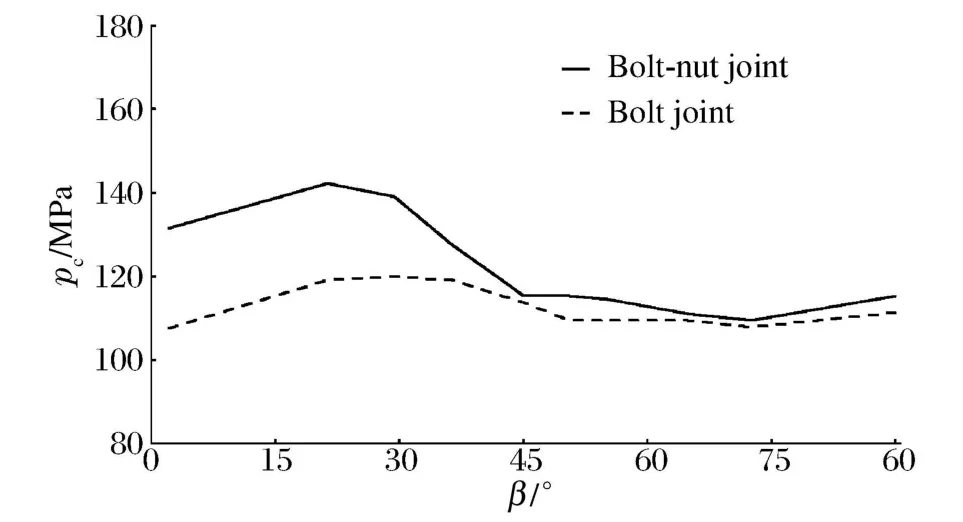
图7 冲击压力方向角对临界破坏载荷的影响Fig.7 Critical damage load affected by shock directions

对机械系统进行整体冲击响应分析时,受各种条件的限制不可能将每个连接螺栓都划分为详细的3维有限元模型进行计算。已有的简化螺栓模型往往是通过共节点或者梁单元进行模拟,这种模型无法进行破坏分析。能进行破坏分析的也只是简单的以某个应力值为破坏标准,无法真实模拟螺栓连接的破坏情况,因此需要建立一种简化的螺栓连接模型来模拟破坏分析中的螺栓连接。

根据3维模型的计算结果,本文中提出用单个实体单元建立螺栓简化破坏模型。在使用整体模型分析系统冲击响应时,不考虑螺栓内部应力状态,只关心连接破坏时被连接件所受应力以及被连接件的相对位置是否真实。LS-DYNA中对此单个单元使用各向异性材料模型,设定各个方向的弹性模量和剪切模量,使发生破坏时单元变形及被连接件应力值与用3维有限元模型的计算结果基本相同。基本步骤为:（1）用3维螺栓有限元模型模拟螺栓连接冲击破坏状态;（2）在后处理软件中测量发生破坏时的螺栓拉伸变形量ΔLz和剪切变形量ΔLx;（3）计算螺栓破坏临界塑性正应变ε和剪切应变γ;（4）建立单个单元简化模型,此单元截面积与螺栓小径截面积基本相同;（5）使用LS-DYNA中的各向异性材料模型,调整各个方向的弹性模量Eij和剪切模量Gij的数值,使单元失效时的塑性变形与用3维模型的计算结果吻合。此方法获得的是准确的螺栓连接部位的平均应力值,但如果连接处有应力集中等情况,需要获得此处精确应力值,分析中不适用此简化模型。

5 结 论

（1）对预紧螺栓连接建立了符合实际情况的3维有限元模型,分析了螺栓连接在爆炸冲击状态下的动态响应规律。（2）冲击波对螺栓连接的破坏与冲击波入射角度密切相关。斜向入射冲击波对螺栓自身的影响最大;而连接件传递冲击时,同等受冲击面积时接近90°方向的入射角最容易产生破坏。在同等冲击波压力峰值作用下,连接件传递冲击破坏大于其自身遭受的冲击破坏。因此在布置重要螺栓安装位置时应尽量减小可能的冲击波作用面积。（3）预紧力的大小无论对自身冲击结果还是传递冲击效果影响都不大,因此在冲击破坏计算时螺栓连接可以不施加预紧力。（4）螺栓-螺母连接的抗冲击能力要强于同等直径的螺栓连接,因此应尽量使用螺栓-螺母连接。（5）基于3维螺栓有限元模型的计算结果,建立了螺栓破坏简化模型。此模型能够模拟螺栓破坏时连接部件的相对位置及被连接件受力情况,但应用有局限性。

[1] 李晓彬,杜志鹏,夏利娟,等.空中爆炸下舰船桅杆结构动态响应的数值模拟[J].船舶力学,2006,10（4）:133-139.

LI Xiao-bin,DU Zhi-peng,XIA Li-juan,et al.Numerical simulation of the dynamic response of vessel mast structure under air explosion[J].Journal of Ship Mechanics,2006,10（4）:133-139.

[2] Hallquist J O.LS-DYNA Theoretical Manual[M].California:Livemore Software Technology,1998:716-717.

[3] 胡昌明,贺红亮,胡时胜.45号钢的动态力学性能研究[J].爆炸与冲击,2003,23（2）:188-192.

HU Chang-ming,HE Hong-liang,HU Shi-sheng.A study on dynamic mechanical behaviors of 45 steel[J].Explosion and Shock Waves,2003,23（2）:188-192.

[4] 张红兵,杜建红.有限元模型中螺栓载荷施加方法的研究[J].机械设计与制造,1999,6（1）:32-33.

ZHANG Hong-bing,DU Jian-hong.Study on the method of applying load of bolt in the finite element model[J].Machinery Design&Manufacture,1999,6（1）:32-33.

[5] 石秀勇,李国祥,胡玉平.发动机飞轮螺栓的三维有限元计算分析[J].中国机械工程,2006,17（8）:845-848.

SHI Xiu-yong,LI Guo-xiang,HU Yu-ping.3D finite element analysis on flywheel bolt of engine[J].China Mechanical Engineering,2006,17（8）:845-848.

[6] 吴新跃,郑建华.舰用机械基础[M].武汉:海军工程大学,2000:157-174.

[7] Balden V H,Nurick G N.Numerical simulation of the post-failure motion of steel plates subjected to blast loading[J].International Journal of Impact Engineering,2005,32（3）:14-34.