反应金属冲击反应过程的理论分析*

张先锋,赵晓宁,乔 良

（南京理工大学智能弹药技术国防重点学科实验室,江苏 南京 210094）

1 引 言

反应金属又称含能金属,是指将1种或多种金属以一定工艺方法组合形成的具有一定强度、硬度和密度的多功能含能结构材料,这类材料在一定条件下（特别是高速冲击作用下）可发生反应生成新的产物并伴随强烈的放热过程。反应金属可以是铝热剂、金属间化合物、金属聚合物、亚稳态分子化合物、矩阵材料及氢化物等[1]。反应金属在冲击作用下的反应行为最早作为材料爆炸烧结课题而被提出来,如NiTi等记忆合金的爆炸烧结。随着反应金属应用价值的日益显著,特别是利用反应金属所制备的活性毁伤元（活性破片、活性聚能药形罩）在提高对目标毁伤效能方面具有较大的潜力,反应金属冲击反应行为得到了广泛关注。受材料种类、微观特性、致密程度以及冲击波特性等的影响,反应金属在冲击波作用下可能出现如下情况:（1）冲击波幅值过小或脉冲时间不足以使材料发生反应,仅使材料致密化及组织均匀化;（2）反应金属在冲击作用下完全发生反应;（3）在冲击压力作用下反应金属部分发生反应,反应过程因压力的卸载而停止;（4）在冲击作用下反应金属部分发生反应,压力卸载后反应继续进行。近30年来学者们开展了大量有关于反应金属冲击反应行为的研究工作。早期工作主要集中于冲击条件下不同组分的粉末混合物发生反应并且生成新的产物[2-3]。进入20世纪90年代,反应金属冲击响应及反应机制得到了深入而广泛的研究[4-7],主要采用宏观与细观相结合的方法研究反应金属的冲击响应行为,主要从反应过程实验观测与数值模拟2方面进行研究,并建立了相应的理论模型。近几年来对反应金属的冲击响应行为研究工作主要集中于反应金属在典型战斗部上的应用验证实验上[8-10]。

本文中在1维冲击波理论基础上分析不同密实度的反应金属的响应行为,结合粉末材料冲击温度及冲击反应的化学动力学方法,提出考虑反应效率的冲击反应理论模型。

2 反应金属冲击状态分析计算

反应金属撞击目标时,撞击瞬间界面处分别向反应金属及靶板传出冲击波。初始冲击波在金属中传播时将会因摩擦等原因使其强度和波长发生衰减而减弱。很高压力下,材料可能发生液化或汽化,体积增大;较低压力下,反应金属及靶板材料都受到强烈压缩。为了简化问题按1维处理,设撞击过程中初始冲击波的传播适用于1维冲击波理论。此处只考虑反应金属内的冲击波传播,忽略靶板的响应。

2.1 初始冲击波的产生

设反应金属以速度v撞击静止的靶板,反应金属及靶板中所产生的冲击波速度分别为us1和us2。在碰撞前反应金属所有粒子具有相同的速度v,碰撞时,金属压缩区的粒子速度减小为up1,方向与初始速度相反,粒子合速度为v-up1。在靶板内碰撞后粒子速度为up2。由界面连续条件[11]

同时利用反应金属及靶板冲击波前后质量、动量守恒,可得到反应金属及靶板中初始冲击波压力表达式分别为

式（1）～（2）中有 5个未知数,为了求解,必须增加材料的状态方程,此处利用线性 Hugoniot关系来表示材料中冲击波速度与质点速度之间的关系

由此可得靶板冲击波质点速度的计算式

2.2 反应金属状态方程参数的确定

利用质量平均方法来确定混合物的状态方程参数

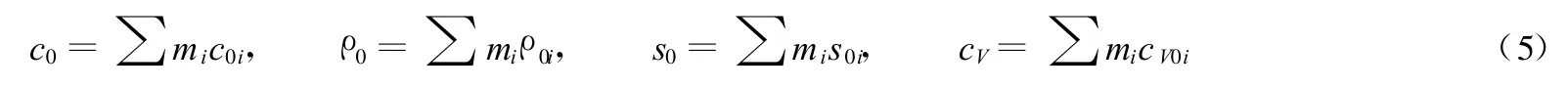
式中:c0为密实度为1时的Hugoniot经验常数,多孔材料孔隙的存在将大大衰减介质中的波速。因多孔介质对冲击波呈指数衰减[12],对多孔介质的声速定义如下

式中:cair为声速,δ为材料的密实度。

2.3 基于上述模型的计算结果

以铝热剂（Al+Fe2O3）及Ni+Al反应为例,反应物的 Hugoniot系数如表1所示[11]。由此可以计算不同密实度的铝热剂（2Al+Fe2O3+PTFE）及 3Al+Ni材料以不同速度撞击钢质靶板所形成的初始冲击波压力,如图1所示,表 2给出了基于本文模型的计算结果与已有的实验数据[13-14]的对比。

从上述的计算结果可以看出:（1）随着冲击速度的提高,在密实度较低的情况下,初始冲击压力增大较慢;随着密实度增大,初始冲击压力增大加快。说明多孔介质的初始孔隙吸收了部分的冲击能量。（2）与已有的实验数据[13-14]比较可知,采用本文中给出的初始声速计算式能够较准确地计算多孔疏松介质的初始冲击波参量。

表1 几种材料的Hugoniot系数Table 1 Hugoniot parameters for several materials

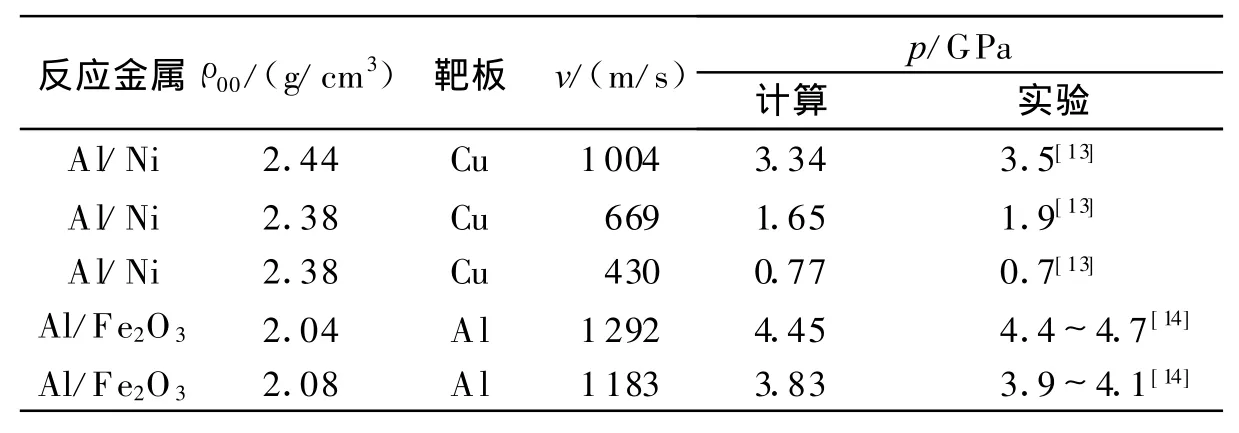
表2 冲击压力的计算结果与实验结果的比较Table 2 Comparison of computational and experimental shock pressures

3 反应金属冲击响应及温升分析

由于反应金属的冲击反应过程复杂,冲击反应过程中存在材料的破碎、侵蚀等,为了方便分析问题,采用如下假设:（1）反应金属的反应仅决定于冲击所引起的材料温度升高,即材料仅对热敏感;反应金属材料在高速撞击时产生高压冲击波,由于冲击波的作用引起材料的压缩、孔隙压垮、颗粒间的摩擦等,由此产生温度的升高,最终诱发材料发生化学反应。（2）由于冲击引发的化学反应过程快,通常在微秒量级内完成,假设反应金属的冲击反应过程是绝热过程,冲击波的加载与卸载是等熵的。（3）问题为准1维过程,与反应金属撞击轴线相垂直的平面上,任意物理量具有相同的值。

根据上述分析将反应金属的冲击反应过程分解为如下几个步骤:

（1）反应金属材料在冲击作用下产生压缩,反应组分间产生强烈挤压作用并伴随界面温度的升高。由于冲击作用过程较短,此阶段只存在材料间的碰撞与摩擦升温,未发生化学反应。

（2）由于温度升高导致反应金属间产生反应,并伴随强烈的放热过程。反应速率与材料冲击温升结果有关,反应效率决定于反应速率和时间。同时冲击作用使材料温度继续升高。

（3）伴随化学反应过程冲击波继续作用,此过程可视为带化学反应的冲击作用过程。

图1 撞击速度与初始冲击波压力的关系Fig.1 Initial shock pressure as a function of impact velocity

3.1 反应金属在冲击作用下的响应过程

冲击波在流体弹塑性介质中传播时,稀疏作用、介质中存在的摩擦以及多孔介质的吸能作用等使冲击波压力衰减,相应波长增加。

在传播距离x上,衰减冲击波压力表达式为[15]

式中:η为冲击波压力衰减系数,由实验确定。对多孔铝,当δ=0.396时,η=296[12]。

从前述的反应金属在冲击载荷作用下的响应行为,冲击载荷对粉末材料的作用效果首先表现为使金属产生压缩。根据质量、动量及能量守恒方程,并假设初始压力p0远小于冲击压力。对于反应金属材料,有

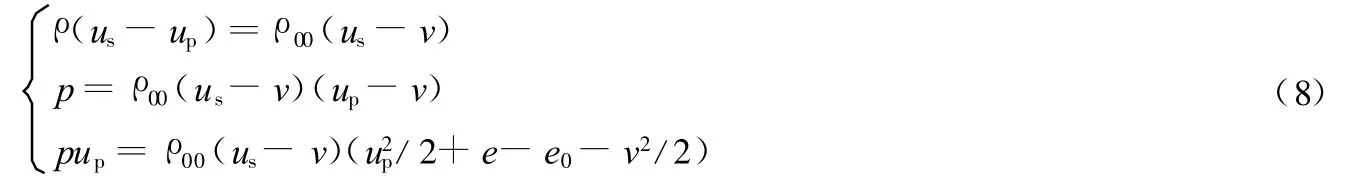
式中:ρ00、ρ分别为反应金属材料初始密度及冲击作用下的密度;us、up分别为冲击波速度和粒子速度;v为初始冲击速度;p为冲击压力;e0、e为初始比内能和瞬时比内能。

能量守恒方程更一般的形式可写为

由方程（7）～（9）和反应金属材料的状态方程,即可求解反应金属材料任意时刻冲击波参数。

3.2 反应金属冲击温升过程分析计算

冲击波作用于反应金属材料时,导致材料的强烈压缩,并引起温度升高,在冲击波波阵面上,假设力学过程是绝热的。由于固体反应物和产物的Hugoniot曲线差异小,通常假设从冲击状态到卸载状态过程是等熵的。材料的冲击温度可以写成如下的形式[13]

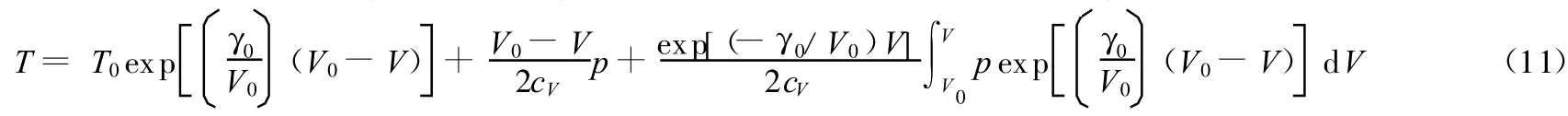
结合冲击所产生的压力及比容的变化,并通过数值计算方法,可以较容易求解冲击波压缩所达到的温度。图2为2种典型冲击反应材料在不同冲击压力下反应金属由冲击所达到的温度。不同撞击速度下,不同密实度的反应金属的冲击温度计算结果如图3～4所示。由图2～4可以看出:

（1）随密实度的增大,同一压力条件下,反应金属材料的冲击温度增大。这是因为,与密实材料相比,存在一定孔隙率的反应金属具有较大的初始比容,从而冲击压缩特性与一般材料的不同。将一定孔隙率的反应金属冲击压缩到与其相应的密实材料具有同一终态比容或压力,所需的冲击压力和能量要高得多,反应金属内部将产生更高的冲击温度。

（2）随着密实度的增大,反应金属的温度分布趋向均匀。这主要是由于随着密实度的增大,反应金属对冲击波的衰减减弱,最终导致了冲击温度的变化。

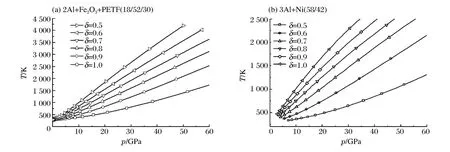
图2 冲击温度与冲击压力的关系Fig.2 Shock temperature as a function of shock pressure

图3 δ=0.7时的冲击温度分布Fig.3 Shock temperature distribution when δ=0.7

图4 v=1 800 m/s时的冲击温度分布Fig.4 Shock temperature distribution when v=1 800 m/s

4 反应金属冲击反应过程

4.1 基于冲击温升的反应过程模型

根据对以铝热反应为代表的反应金属反应放热的DSC分析[16-17],反应金属释放能量的速率定义为

式中:Z为指前因子;Ea为反应材料的表观活化能;T为冲击温度;R为气体常数。利用实验数据[18]对指前因子进行计算

式中:β为升温速率,Tr为实验研究中主放热峰所对应的温度,其余参数同前。根据文献[19],Al+Fe2O3的表观活化能为486.81 kJ/mol,求出指前因子为2.105 3×1018。

反应效率可采用下列计算式式中:k为反应速率,n为根据实验测定的常数,参考文献[20]的定义,n=0.10。

由式（12）～（14）,并结合前述冲击温度的计算结果,可以求得不同冲击速度下2种典型反应金属的反应速率。

由于冲击过程中发生的化学反应伴随发热效应,根据M.B.Boslough[13]的金属冲击反应放热理论模型,并考虑不同冲击温度引起的反应效率因子y,得到反应金属的Hugoniot方程、反应放热的温度方程如下

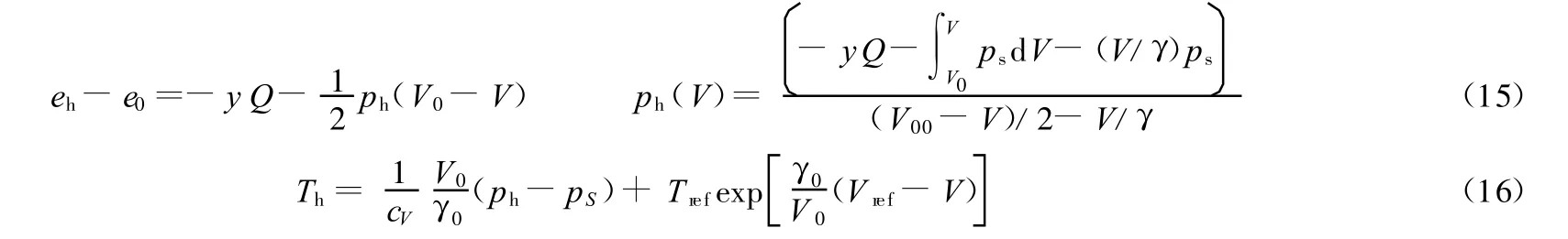
式中:Q为反应金属材料由于冲击反应所释放的能量,其余参数同前。

4.2 基于上述模型的计算结果与分析

铝热反应的化学方程式为2Al+Fe2O3=Al2O3+2Fe-3.97 kJ/g。

利用式（15）～（16）可以求解得到在不同密实度条件下冲击压力影响反应速度及反应效率的结果如图5～6所示。图7为冲击作用时间为1 s时,不同冲击压力与冲击反应温度的关系。反应金属物最终温度（冲击温升与反应温升）与冲击速度计算结果如图8所示。基于上述计算模型对已有的实验结果[21,13]进行了计算,计算结果如表3所示。

从上述计算结果可以看出:

（1）冲击压力对反应金属反应速率影响较明显,随着冲击压力的提高（直接体现为冲击速度的变化）,反应速率显著提高。对（2Al+Fe2O3）反应体系而言在冲击速度超过2 000 m/s时,在1 ms内可达到较高的反应效率。

（2）与不考虑材料反应行为的计算结果相比（仅为材料的冲击温升）,考虑材料反应效率的计算结果较真实地反映了反应金属材料在不同冲击压力的响应行为。且随冲击压力的增加,由于材料反应放热所导致的温度增加较为明显。

（3）随着冲击速度增加,反应金属材料最终温度变化较显著,撞击速度超过2 000 m/s时,材料在较短的时间（0.2 ms）内即可达到较高的反应效率,反应物最终温度也较高。

表3 冲击化学反应结果与已有实验结果比Table 3 Computational and experimental shock temperatures with chemical reaction

图5 反应速率与冲击速度的关系Fig.5 Reaction rate as a function of impact velocity

图6 反应效率随时间的变化Fig.6 Reaction efficiency as a function of time

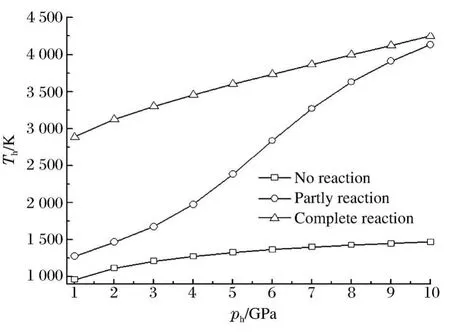
图7 冲击反应温度与冲击压力的关系Fig.7 Shock reaction temperature as a function of shock pressure

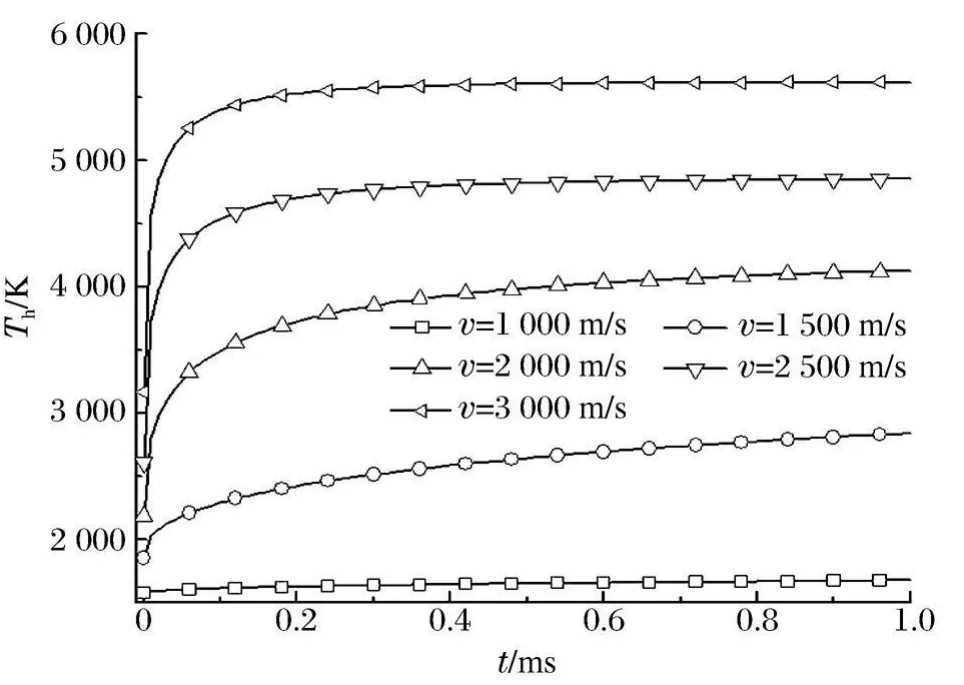
图8 冲击反应温度随时间的变化Fig.8 Shock reaction temperature as a function of time

5 结 论

（1）基于已有的反应材料冲击反应过程理论模型,结合反应材料有关反应速率及效率的研究成果,建立了考虑反应金属材料反应效率的冲击反应理论模型,结合该模型进行相关分析计算,并与已有的实验结果进行了对比,结果表明计算结果是可信的。（2）反应材料冲击升温和反应放热实际上是同时进行的,伴随着复杂的作用过程,而且材料的微观特性（如粒度、改性处理等）都将影响反应金属的冲击反应行为及其结果。

下一步工作重点将材料的化学反应动力学与冲击力学相结合,以期获取更可信的研究结果。

[1] Committee on Advanced Energetic M aterials and Manufacturing Technologies,National Research Council.Advanced Energetic Materials[M].Washington:the National Academy Press,2004.

[2] Psakhie S G,Skripnyak V A.Shock Induced Chemical Processing[M].US:Army Research Office,1996.

[3] Meyers M A.A fundamental study of shock-induced chemical reactions[R].A842003,1994.

[4] Thadhani N,Chen E.Shock synthesis of materials workshop held in Atlanta[R].A148003,1995.

[5] Merzhanov A G.Combustion and explosion processes in physical chemistry and technology of inorganic materials[J].Russian Chemical Reviews,2003,72（4）:289-310.

[6] Ferranti L,Thadhani N N.Dynamic Impact Characterization of Al+Fe2O3+30%Epoxy Composites Using Time Synchronized High-speed Camera and VISAR Measurements[M].US:M aterials Research Society,2006:588-593.

[7] Tomar V,Zhou M.Molecular dynamics simulations of shock-induced thermite reaction[J].Materials Science Forum,2004,465:157-162.

[8] 黄辉,王泽山,黄亨建.新型含能材料的研究进展[J].火炸药学报,2005,28（4）:9-13.

HUANG Hui,WANG Ze-shan,HUANG Heng-jian.Researches and progresses of novel energetic materials[J].Chinese Journal of Explosives&Propellants,2005,28（4）:9-13.

[9] 徐锦仁,何宝国.含能反应式破片材料用于舰船反（高）超音速导弹的设想[J].水雷战与舰船防护,2006（4）:69-72.

[10] HE Yuan,PAN Xu-chao,HE Yong.Explosible fragment shock initiation investigation[C]//Proceedings of International Conference on Mechanical Engineering and Mechanics.2007:1094-1199.

[11] 张庆明,刘彦,黄风雷,等.材料的动力学行为[M].北京:国防工业出版社,2006.

[12] 程和法,黄笑梅,许玲.泡沫铝镁合金的压缩与吸能性的研究[J].兵器材料科学与工程,2002,25（6）:12-14.

CHENG He-fa,HUANG Xiao-mei,XU Ling.Investigation of the compressive properties of the foamed Al-Mg alloy[J].Ordnance Material Science and Engineering,2002,25（6）:12-14.

[13] Boslough M B.A thermochemical model for shock-induced reactions（heat detonations）in solids[J].Journal of Chemical Physics,1990,92:1839-1843.

[14] Eakins D,Thadhani N N.Shock-induced reaction in a flake nickel+spherical aluminum powder mixture[J].Journal of Applied Physics,2006,100:113-121.

[15] Frenkel J.Theory of Liquid[M].London:Oxford University Press,1946:110.

[16] Wang H,Pring A,Ngothai Y,et al.A low-temperature kinetic study of the exsolution of pentlandite from the monosulfide soild soulution using a refined avrami method[J].Geochimica et Cosmochimica Acta,2005,69（2）:415-419.

[17] Kanury A M.A kinetic model for metal+nonmetal reactions[J].Metallurgical Transactions:A,1992,23:2349-2354.

[18] 王毅,姜炜,程志鹏,等.纳米Cu/Al-WO3亚稳态复合材料热反应机理分析[J].物理化学学报,2007,23（11）:1753-1759.

WANG Yi,JIANG Wei,CHEN Zhi-peng,et al.Thermal performance investigation of core-shell Cu/Al micronnano composites with WO3[J].Acta Physico-chimica Sinica,2007,23（11）:1753-1759.

[19] 王毅,姜炜,程志鹏.核壳结构Ni（Cu,Co）/Al微纳米复合粒子的制备及其与Fe2O3的热反应性能表征[J].稀有金属材料与工程,2008,37（7）:1198-1203.

WANG Yi,JIANG Wei,CHEN Zhi-peng,et al.Preparation of core-shell Ni（Cu,Co）/Al micron-nano composites and characteristics of thermite reactions with Fe2O3[J].Rare MetalM aterials and Engineering,2008,37（7）:1198-1203.

[20] Umbrajkar S M,Schoenitz M,Dreizin E L.Exothermic reactions in Al-CuO nanocomposites[J].Thermo-chimica Acta,2006,451（1-2）:34-39.

[21] Bennett L S,Horie Y,Hwang M M.Constitutive model of shock-induced chemical reactions in inorganic powder mixtures[J].Journal of Applied Physics,1994,76（6）:3394-3399.