爆炸膨胀环的截面尺寸效应*

汤铁钢,李庆忠,刘仓理,桂毓林

（中国工程物理研究院流体物理研究所冲击波物理与爆轰物理国防科技重点实验室,四川绵阳 621900）

1 引 言

爆炸膨胀环实验技术一直以来被用于研究材料在高应变率拉伸加载时的动态性能,包括本构关系和断裂特性。P.C.Johnson等[1]通过爆炸膨胀环实验结果计算了膨胀环材料的流动应力-塑性应变-应变率响应;C.R.Hoggatt等[2]运用爆炸膨胀环实验技术,测试了许多工程材料的本构关系数据。由于需要对膨胀环的位移历史进行2次微分,数据的精度一直困扰着膨胀环实验技术的广泛应用。R.H.Warnes等[3]利用激光速度干涉仪（VISAR）直接测量爆炸膨胀环的径向膨胀速度,克服了求流动应力时位移关于时间2次微分的困难,使膨胀环技术得以推广。近年来,对于爆炸膨胀环实验的数值模拟研究逐渐开展起来,F.Llorca等[4]通过数值模拟研究了膨胀环中的应变历史与速度历史,A.Pandolfi等[5]利用3维有限元程序研究了膨胀环的破碎问题。无论实验研究还是数值模拟研究中,大都采用正方形截面的膨胀环,截面边长为1～3 mm。由于正方形截面膨胀环在冲击加载下的运动不稳定,影响了实验数据的精度,F.Llorca等[4]在实验中采用了在膨胀环两侧加约束环的方法解决这一问题。

当截面特征尺寸远小于环向特征尺寸时,膨胀环为小截面尺寸的圆环结构的膨胀过程被近似认为满足1维拉伸应力状态。实际上,处于冲击加载下的膨胀环的内表面往往会在冲击加载早期发生塑性变形,然后才持续径向膨胀,早期的加载过程显然不满足1维应力状态,因此加载早期的数据通常在数据处理时不予采用。膨胀环截面尺寸不同,膨胀行为也会有所不同,将直接影响材料应力-应变-应变率关系的计算。膨胀环截面尺寸的设计没有统一的标准,如何选择合适的截面尺寸,既有利于实验的测试,又不明显影响1维应力状态假定,目前还未见报道。本文中,将利用已有的实验结果及数值模拟对膨胀环的截面尺寸效应进行研究。

2 膨胀环运动分析

爆炸膨胀环实验装置可见文献[6]。驱动器在爆炸产物压力作用下向外膨胀变形,应力波由驱动器传进膨胀环,膨胀环中的应力波到达外边界自由面时反射为拉伸卸载波,质点速度倍增。由于膨胀环与驱动器材料的阻抗不匹配,当膨胀环中的拉伸波返回到驱动器与膨胀环的界面上时,膨胀环将脱离驱动器进入自由膨胀阶段。在自由膨胀阶段,膨胀环中的径向应力很小,近似看作0,因此膨胀环仅在环向应力作用下做减速运动。

对于自由膨胀阶段的膨胀环（如图1所示）,取其中任意环向单元建立运动方程

图1 膨胀环运动分析示意图Fig.1 Movement analysis for an expanding ring

式中:σ为环向应力;R为膨胀环外半径;R0为膨胀环初始外半径;r为膨胀环内半径;r0为膨胀环初始内半径;z为膨胀环宽度;z0为膨胀环初始宽度;ρ为膨胀环材料密度。

假定材料不可压缩,而且膨胀环的厚度相对很小,R与r近似相等,式（2）可以简化表示为

膨胀环的应变、应变率分别为

在运动分析中假定膨胀环的厚度很小,这是膨胀环实验设计的基本条件。明显地,膨胀环的宽度将影响膨胀环中的轴向应力,而由运动方程的求解,轴向应力对膨胀环的运动没有影响,膨胀环的运动规律取决于膨胀环中的应力状态。事实上,利用膨胀环实验直接求解的是环向应力,由于求解过程中假定了1维应力状态,忽略了径向应力和轴向应力,以此作为膨胀环材料的流动应力进行本构关系的计算。因此,无论存在径向应力还是轴向应力,都会对实验结果的数据处理造成影响。

3 计算模型与本构参数

采用3维动力学有限元程序LS-DYNA对爆炸加载下膨胀环的尺寸效应进行数值模拟,计算模型如图2所示。中心柱形装药为密度1.05 g/cm3的PETN,直径10 mm,采用JWL状态方程;装药容器厚度3 mm,材料为PMMA;驱动器厚度12 mm,材料为20钢;膨胀环内径 40 mm,厚度1 mm,材料为无氧铜T U1。网格划分时,膨胀环的特征网格尺寸为0.5 mm,其他部件的特征网格尺寸为1.0 mm。

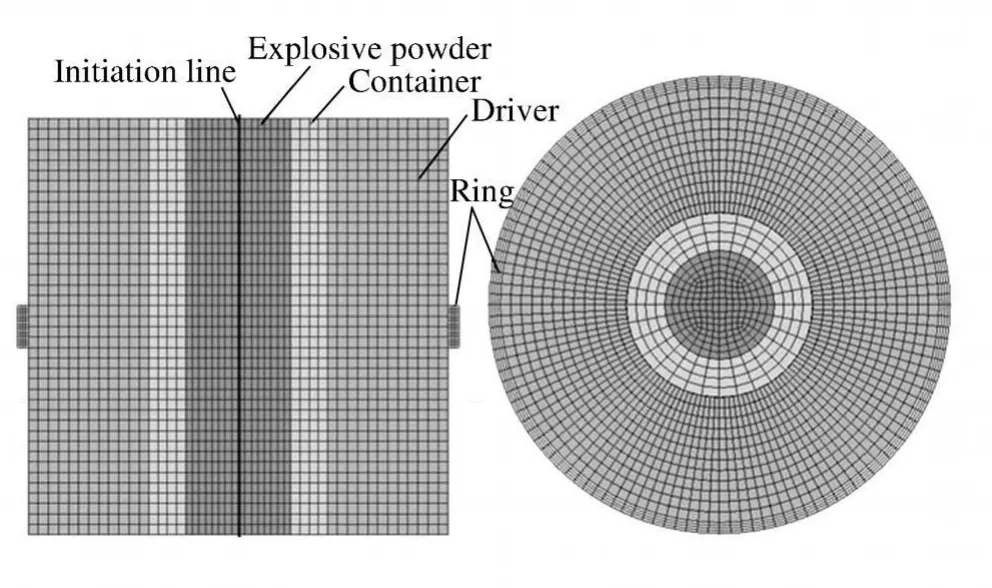
图2 计算模型Fig.2 Computational model

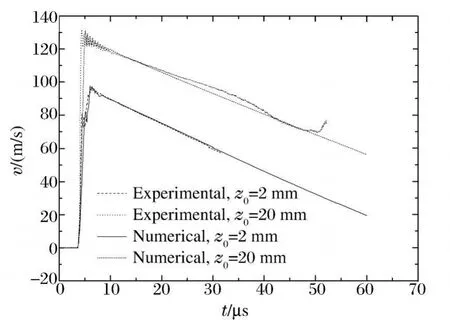
图3 膨胀环膨胀速度Fig.3 Velocities of rings

20钢和无氧铜均采用J-C本构模型,利用文献[7]中的无氧铜J-C本构模型关系参数对膨胀环的膨胀过程进行计算,计算速度曲线与实验曲线偏离较大,即速度斜率不同,而速度斜率（加速度）正是利用膨胀环实验数据计算本构关系的敏感参数。利用已有的实验数据（膨胀环宽度为2 mm）对无氧铜的JC本构模型中的硬化指数n和应变率因数C进行修正,修正后的计算速度历史与实验结果的比较见图3,两者符合较好。同时计算了宽度20 mm膨胀环的膨胀过程,炸药直径为12 mm,计算的速度历史与实验曲线也符合较好,说明修正后的参数可以用于膨胀环的运动规律计算。20钢与无氧铜的J-C本构模型参数见表1。表中,ρ为密度,cp为比定压热容,E为杨氏模量,ν为泊松比,A为屈服应力,B为硬化常数,n为硬化指数,C为应变率因数,m为热软化指数。

表1 20钢和无氧铜的本构模型参数Table 1 Constitutive parameters for 20 steel and copper

在实验中膨胀环的宽度越小,越能满足假定条件。实际上膨胀环的宽度太小时,在实验中存在2个不利因素:1个是由于边界稀疏严重影响,加载速度峰值上不去;另1个是加载过程中膨胀环膨胀运动不稳定,容易发生侧向翻转,影响实验数据的精度。

4 计算结果分析

对膨胀环尺寸效应的计算分析中,采用相同的加载条件,即炸药直径均为10 mm,装药容器与驱动器的尺寸也都完全一致,计算中膨胀环厚度为1 mm,仅改变膨胀环的宽度,膨胀环宽度分别取1、2、4、6、8和20 mm。截面1 mm×1 mm的膨胀环最能满足1维应力状态的假定,称为标准膨胀环,以它作为基准,分析膨胀环宽度变化对运动规律及内部应力状态的影响。

4.1 膨胀环宽度对膨胀速度的影响

膨胀环的速度历史如图4所示。膨胀环的速度历史是反演材料本构关系的主要依据,也是实验中能直接测量的参数。速度的大小和斜率是反映材料本构关系特征的2个因素,速度的大小反映了加载强度（或加载应变率）,速度的斜率反映了材料在此应变率下的动态特性。

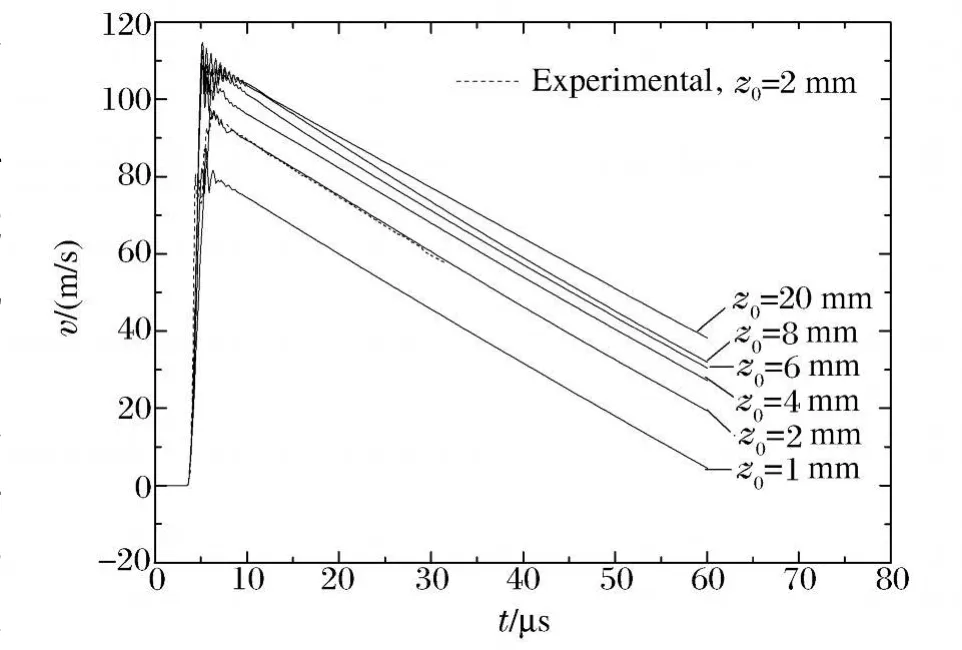
图4 不同宽度时膨胀环膨胀速度Fig.4 Velocities of rings with different width

从速度历史看,膨胀速度峰值随着膨胀环宽度的增加而增加,当宽度大于8 mm后,速度峰值不再增加。在相同加载条件下,膨胀环的宽度增加使其膨胀速度峰值增加。这是因为宽度的增加减少了边界稀疏的影响,提高了冲击能量的利用效率。

从速度的斜率看,膨胀环宽度为2 mm时,速度曲线特征与标准膨胀环完全一致。当膨胀环宽度增加至4 mm时,膨胀环膨胀早期的速度曲线特征有所变化,呈现向下弯曲的特征,后期速度斜率基本上仍与宽度1、2 mm膨胀环的速度曲线平行。当膨胀环宽度大于4 mm后,速度曲线的斜率发生了明显的变化,不再与标准膨胀环的速度曲线平行。

4.2 膨胀环宽度对应力状态的影响

膨胀环实验时,忽略了膨胀环中的径向应力和轴向应力,采用环向应力表征流动应力（等效应力）进行本构关系的拟合,环向应力与等效应力的符合程度也是反映实验是否满足1维应力状态的判据。不同宽度膨胀环的环向应力和等效应力的比较,如图5所示。

图5 膨胀环的环向应力和等效应力Fig.5 Hoop stress and effective stress in expanding rings

由于不同宽度的膨胀环获得不同的膨胀速度峰值,因此其屈服应力的幅值也不一致,这是材料强度的的应变率效应,不影响对尺寸效应的分析。从环向应力的特征看,只有宽度2 mm的膨胀环中的环向应力特征与标准膨胀环基本相似,在加载早期存在明显的卸载过程,而且在整个自由膨胀过程中,环向应力与等效应力符合很好。当膨胀环宽度增加至4 mm及以上时,加载早期不再有明显的卸载过程;当膨胀环宽度增加至6 mm及以上时,环向应力与等效应力在较长时间段内不吻合,不能再用环向应力来表征等效应力。

随着膨胀环宽度的增加,环向应力与等效应力的偏差越来越大,说明另外2个主应力已经不可忽略。不同宽度膨胀环的径向应力和轴向应力如图6所示,不同宽度膨胀环中的径向应力只是在加载早期存在差别,幅值与持续时间均随着膨胀环宽度的增加而增加,到中后期所有宽度的膨胀环中的径向应力都衰减为0。轴向应力则在加载早期最大幅值相差不大,衰减速率随着膨胀环宽度的增加而减小。对于宽度2 mm的膨胀环,径向应力和轴向应力的幅值和变化规律均与标准膨胀环保持较好的一致性。

图6 膨胀环的径向应力和轴向应力Fig.6 Radial stress and axial stress in expanding rings

由此看来,膨胀环宽度对于膨胀环的1维应力状态存在明显的影响,随着膨胀环宽度的增加,应力状态逐渐偏离1维应力状态的假定。数值模拟表明:对于厚度1 mm的膨胀环,宽度为2 mm时,速度历史、应力状态的变化规律均与标准膨胀环一致,能较好满足1维应力状态;当膨胀环宽度大于4 mm时,速度历史、应力状态均与标准膨胀环出现明显偏离,不再满足1维应力状态的假定。因此,在爆炸膨胀环实验研究中,适当增加膨胀环的宽度是可行的,这样既可以提高加载应变率,又可以增加膨胀环膨胀运动的稳定性。

5 结 论

利用实验结果修正了无氧铜的J-C本构模型参数,通过3维数值模拟研究了爆炸膨胀环实验中膨胀环宽度变化对运动规律、应力状态的影响,获得以下结论:

（1）膨胀环的宽度对加载速度峰值存在明显的影响,随着膨胀环宽度的增加,加载速度峰值增加;当宽度增加至8 mm后,加载速度峰值不再增加。

（2）膨胀环的宽度对速度斜率有明显影响,宽度不大于厚度的2倍时,速度斜率保持一致。

（3）膨胀环的宽度对3个主应力的幅值及变化规律均有影响,当膨胀环宽度不超过2 mm时,可以较好满足1维应力假定;当膨胀环宽度继续增加时,应力状态不再满足1维假定。

（4）实验研究时,可以适当增加膨胀环的宽度,既可以提高膨胀环的加载应变率,又可以增加膨胀环的运动稳定性。

[1] Johnson P C,Stein B A,Davis R S.Measurement of dynamic plastic flow properties under uniform stress[C]//Symposium on Dynamic Behavior of M aterials.ASTM Special Publication,1963:195-198.

[2] Hoggatt C R,Recht R F.Stress-strain data obtained at high rates using an expanding ring[J].Experimental Mechanics,1969,9（10）:441-448.

[3] Warnes R H,Duffey T A,Karpp R R,et al.An improved technique for determining dynamic material properties using the expanding ring[C]//Meyer M A,Murr L E.Shock Waves and High-strain-rate Phenomena in Metals.New York:Plenum Press,1981:23-36.

[4] Llorca F,Juanicotena A.Expanding ring test:Numerical simulation-application to the analysis of experimental data[J].Journal De Physique IV,1997,7:325-340.

[5] Pandolfi A,Krysl P,Ortiz M.Finite element simulation of ring expansion and fragmentation:The capturing of length and time scales through cohesive models of fracture[J].International Journal of Fracture,1999,95:279-297.

[6] 汤铁钢,李庆忠,陈永涛,等.实现材料高应变率拉伸加载的爆炸膨胀环技术[J].爆炸与冲击,2009,29（5）:546-649.

TANG Tie-gang,LI Qing-zhong,CHEN Yong-tao,et al.An improved technique for dynamic tension of metal ring by explosive loading[J].Explosion and Shock Waves,2009,29（5）:546-649.

[7] Johnson G R,Cook W H.Fracture characteristics of three metals subjected to various strains,strain rates,temperatures,and pressures[J].Engineering Fracture Mechanics,1985,21（1）:31-48.