半球阻波结构体底部的约束形式*
李晓杰,秦小勇,闫鸿浩
(1.大连理工大学工业装备结构分析国家重点实验室,辽宁大连 116023;
2.大连理工大学土木工程学院岩土工程研究所,辽宁大连 116023)
1 引 言
目前,我国有大小爆炸加工厂家80余家,爆炸焊接复合板总产值达40多亿人民币。由于复合板生产的需要,10~20 m2的大板幅不锈钢复合板已成为常用产品,2~3 mm的不锈钢复层通常需要铵油炸药量20~30 kg/m2,因此,10~20 m2的大板幅不锈钢复合板一次爆炸的总炸药量在200~600 kg,有时甚至达到1 000 kg炸药爆炸量。爆炸焊接是在野外地表进行裸露爆炸,爆炸所引起的空气冲击波强度很高,对周围环境会造成一定的影响,使附近环境问题日渐突出;另外,由于是在野外露天生产,爆炸焊接直接受到气候和天气的影响,造成产品质量不稳定、雨季停产等问题。
对冲击波在容器内部的传播及冲击波与壳体的耦合作用已有过研究,如Gupta等用有限差分程序计算了半球容器在29 kg TNT炸药爆炸下的响应;T.A.Duffey等运用有限差分和有限元程序模拟了炸药在球壳中心的爆炸动力响应[1];T.A.Duffey等[2]和B.B.Lewis[3]用DYNA3D进行了数值模拟和实验研究;胡八一等[4]、朱文辉等[5]、钟方平[6]、闫鸿浩等[7]对球形和圆柱形爆炸容器都进行过研究。爆炸容器的流固耦合计算是非常复杂的动力学问题,很难给出解析解,而实验却往往难于涵盖全貌,这时数值计算可以弥补实验的不足[8]。采用LS-DYNA进行大型的爆炸空气冲击波问题的计算,尽管计算结果精度与实际相差较大,但可以获得全场形貌和相对数据,便于规律性的发现。因此为了准确确定这类问题,有效途径应该是实验和模拟相结合。
爆炸焊接半球阻波结构体是一种专门用于爆炸焊接的特殊爆炸洞,主要用于解决爆炸焊接中的冲击波防护和全天候生产问题。由于大多数的爆炸洞均是采用钢壳与钢筋混凝土结构,造价较高。为此,我们与大连爆炸加工研究所合作,借鉴爆炸容器与爆炸洞特点,设计一种专门用于爆炸焊接生产的半球型钢壳覆土抗爆结构,用以部分消除爆炸冲击波和解决全天候生产问题。为确定半球壳与地基基础的连接形式,用LS-DYNA模拟自由放置与刚性连接2种形式。
2 半球阻波结构体底部约束形式数值模拟
爆炸焊接半球阻波结构的设计炸药量为600 kg铵油炸药,主体为掩埋在土中的直径36 m半球壳,球壳为壁厚36 mm的16MnR钢板,入口为直径12 m拱形通道,上部设有直径8 m的排烟口,半球底部自由放置在基础上。为了减少计算量,根据所设计的1/6缩比实验模型来建立数值模型,如图1所示。模型为直径6 m、壁厚6 mm的钢壳,排烟口直径1.333 m、门口直径3 m,半球上覆土厚度为66 cm,密度2.0 t/m3,炸药为5 kg铵油(相当原型上1 080 kg ANFO)。建立如图2的简化计算模型,只考虑炸药、空气与球壳3部分,将覆土直接化为压力静载施加在球壳上,筋板折减强度加在球壳厚度上,门口和排烟口部分定义为无反射边界,将中部对称面与地面设为刚性边界,划分单元总计6 175 888个,其中炸药单元8个,空气单元605 888个,球壳单元11 692个。利用LS-DYNA分析球壳底边仅对垂直方向约束、全约束与自由情况,当计算时程为12 ms时,每种情况耗费机时为约18.73 h。

图1 1/6实验模型Fig.1 The 1/6 experimental model
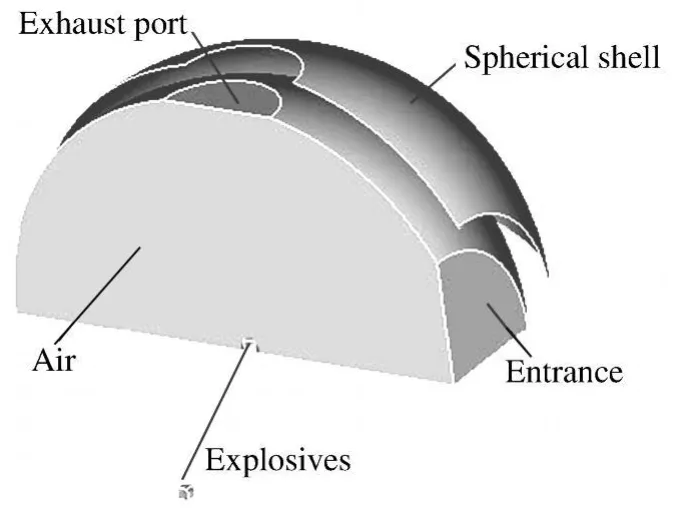
图2 炸药、空气与球壳计算模型图Fig.2 The numerical model of explosives-air-spherical shell
图3为对球壳底部在y方向(地面法向)进行约束时球壳上对应单元点的等效应力时程图。从中可以看出,由于孔口应力集中效应,导致在排烟口和门口的壳体等效应力最大,其中排烟口点C应力最大值为260.68 MPa,点D的应力最大值为259.35 MPa;门底部点B应力最大值为384.70 MPa,门角部点A应力最大值为222.28 MPa;而球面3/4高度点E应力峰值为141.51 MPa,其余各部位的应力峰值均接近160 MPa,门口底部点B应力峰值是其余部位的2倍以上,受力状态明显不合理。另外,尽管一般16MnR钢板屈服强度σs可以达到390 MPa,但是由于材质均匀性与焊接质量原因,一般钢板实际许用应力仅为140 MPa,球壳上的应力明显大于许用应力,在工程上是不允许的。由此可见,必须对孔口部分进行增强处理,并采用其他措施降低球壳应力。
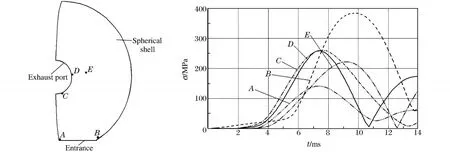
图3 底面y方向约束时球壳上的等效应力时程图Fig.3 Time-histories of equivalent stress on spherical shell under bottom y direction constrained
球底边施加全约束的计算结果见图4。由于应力集中效应,依然在排烟口和门口的壳体等效应力最大,但比底面y方向约束时应力状态有较大的改善。排烟口点D的应力最大值为260.83 MPa,附近点C应力最大值为233.06 MPa;门底部点B应力最大值为266.52 MPa,门角部点A应力最大值为206.34 MPa;而球面3/4高度点E应力峰值为132.10 MPa,其余各部位的应力峰值均接近130 MPa,排烟口点D和门口底部点B应力峰值是其余部位的2倍左右,受力状态依然不合理,进一步说明了孔口部位必须进行补强。
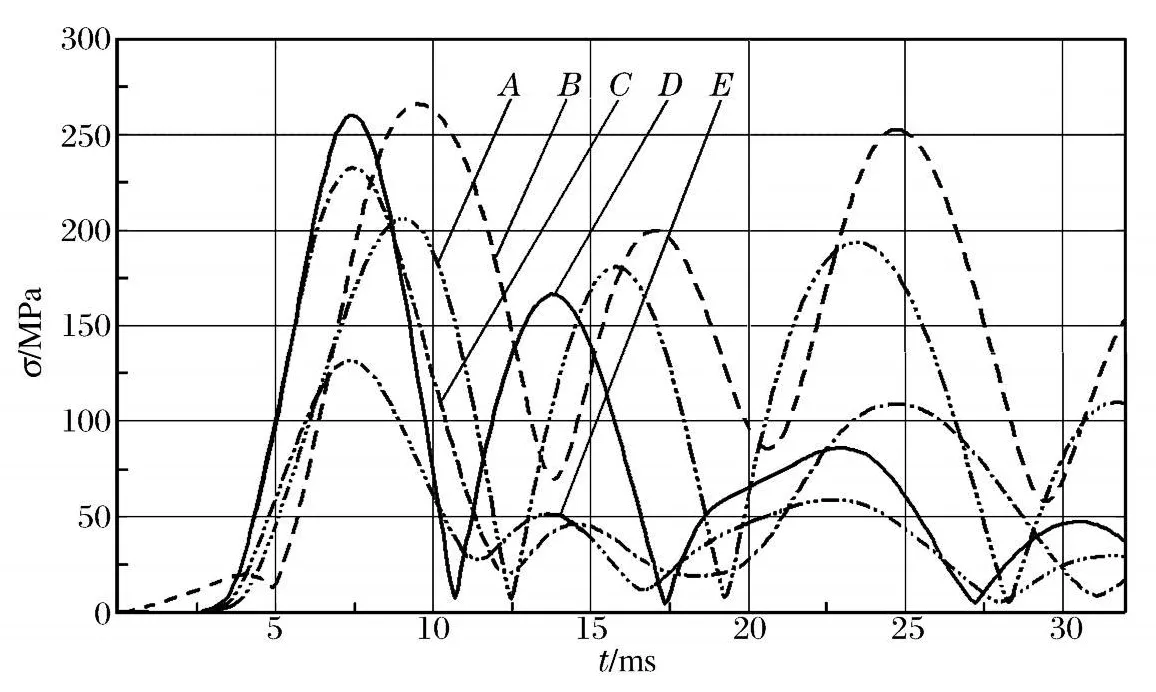
图4 底面全约束时球壳上的等效应力时程图Fig.4 Time-histories of equivalent stress on spherical shell under bottom constrained
基于进一步降低球壳应力考虑,完全解除对球壳底面的约束,计算结果见图5。解除球壳底约束后,尽管排烟口与门口依然存在应力集中效应,但排烟口点D的应力最大值为187.54 MPa,附近点C应力最大值为 183.54 MPa;门顶部点A应力最大值仅为86.87 MPa,其余各部位的应力峰值均接近100 MPa。由计算结果可以看出,只有排烟口边缘点D和C应力较大,其余部分应力小于100 MPa,受力状态得到改善。由此可见,采用球底面自由放置于地面的方法,可以大大降低球壳抗内爆时的应力,如果进一步对排烟口、入口等部位进行适当的补强,完全可以使球壳受力更加合理。同时这种方法将不用考虑球壳如何与地基连接,大大降低了地基处理难度,将大幅度地降低爆炸焊接阻波结构体的造价。
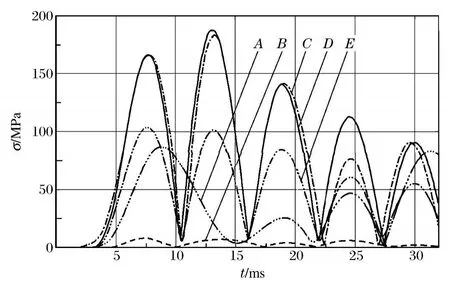
图5 底面无约束时球壳上的等效应力时程图Fig.5 Time-histories of equivalent stress on spherical shell under free bottom
3 底面自由放置半球阻波结构体应力测试结果
考虑到上述LS-DYNA所建立的计算模型较粗糙,而且对于空气中爆炸问题的计算精度很差,为此建立了如图1的1/6缩比实验模型。考虑外压稳定性,在缩比模型上采用了立筋增加球壳刚度;在底部、中部和排烟口都加有环梁,一来保证球壳整体刚度,二来用于补强底部和排烟口的边缘与应力集中部位;出入口采用门柱连接底环梁与中环梁,提高门口强度,降低应力集中。将球壳直接放置在地面上,用砂土掩埋,进行了一系列的爆炸实验。使用铵油炸药,药量为2、3、4和5 kg,对入口的门角、门顶、排烟口边缘、球壳3/4高度等重要部位采用应变花贴片进行了动态应力测试。进行了200余次6 kg药量加强爆炸冲击实验,除球壳3/4高度部位局部焊缝开裂外,球壳整体结构完好。发现焊缝开裂与覆盖砂土震落有关,对焊缝开裂部位进行修补,重新补充砂土,再进行50余次加强爆炸冲击试验,球壳未发现进一步损伤。
应力测试结果表明,采用自由状态放置并对局部应力集中部位进行补强后,球壳的出入与排烟口部分应力状态得到很好的改善,这些部位测得的应力值均小于球壳3/4高度部位。图6~7分别为球壳3/4高度的应力测试结果:图6为5 kg铵油炸药的von-Mises等效应力时程(放大到原型上的对应药量为1 080 kg);图7为3 kg铵油炸药的von-Mises等效应力时程(放大到原型上的对应药量为648 kg)。从应力时程可见,5 kg药量时的应力峰值为253 MPa,远小于16MnR的屈服应力,但大于许用应力;3 kg药量时的应力峰值为132 MPa,小于16MnR许用应力,因此,原型满足600 kg铵油炸药设计。对比实验与计算的应力时程曲线可以看出,数值计算应力峰值与实际测试偏差较大,这正是计算模型较粗糙和LS-DYNA对空中爆炸问题计算精度差2方面引起的;另外,实验与计算的应力波动时间衰减情况也不完全一致,实测曲线只有1~2个较大的峰值,应力随时间的衰减比计算曲线要快得多,究其原因,是因为在计算模型中将土的作用简单考虑成静载、忽略了土的消振作用所致,如何进一步考虑复杂的土载效应尚需进一步研究。

图6 5 kg硝铵炸药爆炸的等效应力时程图Fig.6 Time-histories of equivalent stress with 5 kg ANFO explosion

图7 3 kg硝铵炸药爆炸的等效应力时程图Fig.7 Time-histories of equivalent stress with 3 kg ANFO explosion
4 结 论
根据简化计算模型,利用LS-DYNA对不同底部约束情况下的爆炸焊接阻波结构体进行了数值模拟。由计算结果分析发现,球壳在排烟口、出入口部位,存在着不同程度的应力集中现象,局部应力远远超出其他部位,应进行局部补强;除排烟口、出入口应力集中部位外,球壳高度约3/4处的应力最大,需作为关键部位考虑。当球壳底部完全自由时,球壳整体的应力水平大大下降,采用球底面自由放置于地面的方法可以进一步提高球壳抗内爆能力。
实验结果表明,对排烟口、出入口部位进行补强降低应力集中后,测试球壳高度约3/4处的应力最大部位与计算结果吻合,这说明尽管计算数值与实际相差较大,但计算模拟可以反映整场全貌,便于发现问题。采用球底面自由放置于地面的方法不仅提高了球壳的抗爆能力,同时也节省了地基处理,大幅度地降低阻波结构体的造价。
[1] 郑津洋,徐平,傅强,等.爆炸容器研究进展和新结构探讨[C]//第二届全国爆炸力学实验技术交流会议论文集.洛阳,2002:243-250.
[2] Duffey T A,Greene J M,Baker W E,et al.Containment of explosions in spherical vessels[R].LA-U R-92-4061,1992.
[3] Lewis B B.Confinement vessel analysis final report[R].LA-SUB-93-241,1992.
[4] 胡八一,柏劲松,张明,等.球形爆炸容器动力响应的强度分析[J].工程力学,2001,18(4):136-139.
HU Ba-yi,BO Jin-song,ZHANG Ming,et al.The dynamic response analysis of spherical explosion-containment vessels[J].Engineering Mechanics,2001,18(4):136-139.
[5] 朱文辉,薛鸿陆,张振宇.解析方法与数值模拟相结合求解炸药在容器内部爆炸产生的壁面载荷[J].国防科技大学学报,1997,19(6):102-106.
ZHU Wen-hui,XUE Hong-lu,ZHANG Zhen-yu.Combining analytical method with numerical simulation to obtain blast load on chamber wall produced by an explosive charge[J].Journal of National University of Defense Technology,1997,19(6):102-106.
[6] 钟方平.双层园柱形爆炸容器弹塑性结构响应的实验和理论研究[D].合肥:中国科学技术大学,1999.
[7] 闫鸿浩,李晓杰,曲艳东,等.爆炸焊接半球结构体的阻波研究[C]//中国力学学会学术大会2007.北京,2007:658.
[8] 霍宏发,于琴,黄协清.组合式爆炸容器冲击载荷及其动力响应数值模拟[J].精密制造与自动化,2003(增刊):39-40.
HUO Hong-fa,YU Qin,HUANG Xie-qing.Numerical simulations of impact loading and dynamical response for assembled explosion vessels[J].Precise Manufacturing&Automation,2003(supple):39-40.

