用VLW状态方程计算水的冲击Hugoniot曲线*

韩 勇,龙新平,蒋治海,黄毅民,何 碧,吴 雄

（1.中国工程物理研究院化工材料研究所,四川绵阳 621900;

2.中国工程物理研究院,四川 绵阳 621900;

3.西安近代化学研究所,陕西 西安 710065）

1 引 言

炸药爆轰性能参数的理论计算对炸药配方设计十分重要,炸药爆轰研究者对此开展了大量的工作。C.L.Mader[1]根据BKW爆轰产物状态方程,编写了BKW程序。其他研究者也开发了基于不同状态方程的爆轰性能参数计算程序,如基于JCZ3状态方程的Tiger[2]、CHEETAH[3]程序,基于WCA状态方程的CHEQ[4]程序等。20世纪80年代,吴雄[5]应用张光鉴[6]的相似理论,提出了一个以L-J势函数为基础的简化维里模型的爆轰产物状态方程,即VLW爆轰产物状态方程,并编制了FORTRAN VLW程序。不同形式的状态方程意味着对理论状态方程不同方式的简化,从而所采用势参数也应有所不同。JCZ3、WCA等状态方程中所选用势参数值均通过与实验压缩数据或分子动力学计算数据相匹配来调节获得[7-9],而我国在VLW状态方程方面尚未进行该方面的工作。在VLW程序中,部分爆轰产物势参数引用文献值,部分爆轰产物根据炸药爆轰性能实验值调整获得[10],并未与该产物的静压或冲击Hugoniot实验数据对比。针对这一不足,本文中结合VLW状态方程,初步开展不同势参数值对计算炸药爆轰产物组分之一的水的冲击Hugoniot曲线的影响研究,并将计算结果与文献实验结果及采用BKW状态方程的计算结果进行比较分析。

2 VLW状态方程及冲击Hugoniot计算原理

VLW状态方程由维里状态方程简化而来,其假设高阶维里系数与低阶维里系数相似,高阶维里系数可通过二阶维里系数求得,进而将维里物态方程以简便形式写出

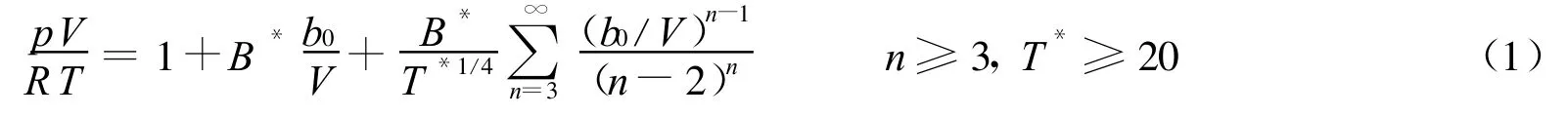
VLW状态方程的第二阶维里系数通过理论计算获得

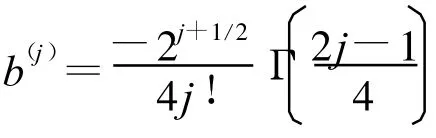
根据热力学理论,若选取独立变量温度T、摩尔体积V,则热力学函数p（T,V）、E（T,V）可从自由能F=F（T,V）导出

结合式（1）、（3）推导可得物质自由能的表达式

式中 :q=B*/T*1/4,w=b0/V,φ0=[（G0-）0+（）0]/（R T）,其中（G0-）0为自由能,为焓。根据式（4）、（5）可得内能E的表达式

物质的冲击Hugoniot关系为

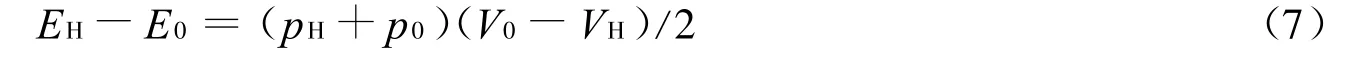
式中:EH、pH、VH分别为物质受冲击后的内能、压力及体积,E0、p0、V0分别为物质的初始内能、压力及体积。

由式（1）、（5）、（6）、（7）即可计算获得物质的冲击Hugoniot曲线。

3 计算结果与讨论

水的初始态参数引用文献值[12]:T0=294.7 K,V0=18.014 cm3/mol,p0=100 kPa,E0=19.757 9 kJ/mol。ε、b0分别取不同参数值,计算获得水的冲击Hugoniot曲线如图1所示。图1（a）中b0=30.42,ε/K=80～ 400;图 1（b）中 ε/K=120,b0=28.0 ～32.0。

图1 水的冲击Hugoniot曲线的计算值与文献值比较Fig.1 Comparison between calculation data and experiment data about Hugoniot curve of water

由图1可得,适当调整势参数的值,可改变计算所得水的Hugoniot曲线位置。当势参数ε/K=120、b0=30.42时,采用VLW状态方程能够与A.C.Mitchell等[13]的实验结果和杨向东等[14]的理论计算结果符合较好。而由文献[15]可得,采用VLW状态方程计算炸药爆轰性能参数时所采用的水的势参数为:ε/K=180、b0=30.42,与我们计算所得的势参数有所差异。然而,VLW程序仍然能够成功计算炸药的爆轰性能参数,这一方面是由于所选用参数与优选参数所得水的冲击Hugoniot曲线相差不大,另一方面也与该程序的开发者在混合法则及部分爆轰产物势参数的调整方面所作的努力分不开。

图2 采用VLW和BKW状态方程计算的水的冲击Hugoniot曲线与文献值的比较Fig.2 Comparison between calculation data by VLW and BKW EOS and experiment data about Hugoniot curve of water

分别采用VLW状态方程及BKW状态方程计算水冲击Hugoniot曲线的结果与文献值的比较如图2所示。VLW状态方程选取2套势参数（ε/K,b0）,分别为（120,30.42）、（180,30.42）;BKW 状态方程选取2种余容值k=250、420。其中,k=250为C.L.Mader[1]拟合水的冲击Hugoniot曲线所选用值,k=420为根据分子结构计算的几何余容。由图2可得,即使当势参数ε/K=180、b0=30.42时,在爆轰条件（压力p一般小于50 GPa）下,VLW状态方程仍然能够比BKW状态方程更准确描述水的冲击 Hugoniot关系,这也进一步证明了采用该套参数预测炸药爆轰性能的有效性。根据2种状态方程的形式分析可得,采用VLW状态方程之所以能够比BKW状态方程更准确地描述水的冲击Hugoniot关系,是因为BKW状态方程是基于维里方程的一级近似建立的,而VLW状态方程的前3项是维里方程的理论式,第4项以后才是经验式,VLW状态方程更趋近于理论状态方程[16]。

4 结 论

（1）通过对势函数参数的调整,采用VLW状态方程可以较好地拟合炸药爆轰产物组分 水的冲击Hugoniot关系曲线;（2）与BKW状态方程相比,VLW状态方程能够更准确地描述水的冲击压缩状态;（3）通过对炸药其他爆轰产物冲击Hugoniot实验数据的拟合,可建立一套基于基础实验、并适用于VLW状态方程的势函数参数。

[1] Mader C L.Numerical modeling of explosives and propellants[M].New York:CRC Press,1998.

[2] Cowperthwaite M,Zwisler W H.The JCZ equations of state for detonation products and their incorporation into the Tiger code[C]//Proceedings of the 6th International Symposium on Detonation.Coronado,California,1976:162-172.

[3] Howard W M,Fried L E,Souers P K.Kinetic modeling of non-ideal explosives with CHEETAH[R].DE200114716,2001.

[4] Ree F H.Statistical mechanical theory of chemically reacting multiphase mixtures:Application to detonation properties of PETN[J].Journal of Chemical Physics,1984,81（3）:1251-1263.

[5] WU Xiong.Detonation performance of condensed explosive computed with the VLW equation of state[C]//Proceedings of the 8th International Symposium on Detonation.Albuquerque,New Mexico,1985:796-804.

[6] 张光鉴.相似论[M].南京:江苏科技出版社,1992.

[7] Hobbs M L,Baer M R,Mcgee B C.Extension of the JCZ product species database[C]//Proceedings of the 11th International Symposium on Detonation.Snowmass,Colorado,1998:958-968.

[8] Fried L E,Howard W M,Souers P C.Exp6:A new equation of state library for high pressure thermochemistry[C]//Proceedings of the 12th International Symposium on Detonation.San Diego,California,2002.

[9] Fried L E,Nir G,I-Feng W K,et al.Non-molecular phases of H2O and HF under detonation-like conditions[C]//Proceedings of the 13th International Symposium on Detonation.Virginia,Norfolk,2006.

[10] 龙新平,何碧,蒋小华,等.论VLW 状态方程[J].高压物理学报,2003,17（4）:247-254.

LONG Xin-ping,HE Bi,JIANG Xiao-hua,et al.Discussions on the VLW equation of state[J].Chinese Journal of High Pressure Physics,2003,17（4）:247-254.

[11] Hirschfelder J O,Curtiss C F,Bird R B.Molecular theory of gases and liquids[M].New York:Wiley,1964.[12] Ree F H.Molecular interaction of dense water at high temperature[J].Journal of Chemical Physics,1982,76（12）:6287-6302.

[13] Mitchell A C,Nellis W J.Equation of state and electrical conductivity of water and ammonia shocked to the 100 GPa（1 M bar）pressure range[J].Journal of Chemical Physics,1982,76（12）:6273-6281.

[14] 杨向东,胡栋,经福谦.炸药爆轰产物液氮液氦和水状态方程研究[J].高压物理学报,1999,13（2）:93-102.

YANG Xiang-dong,HU Dong,JING Fu-qian.Studies of EOS for detonation products:Liquid nitrogen,liquid helium and water[J].Chinese Journal of High Pressure Physics,1999,13（2）:93-102.

[15] 吴雄.新型爆轰产物物态方程[J].高压物理学报,1991,5（2）:98-103.

WU Xiong.A new equation of state for detonation products[J].Chinese Journal of High Pressure Physics,1991,5（2）:98-103.

[16] 吴雄,龙新平,何碧,等.VLW 状态方程的回顾与展望[J].高压物理学报,1999,13（1）:55-58.

WU Xiong,LONG Xin-ping,HE Bi,et al.Review and look forward to the progress of VLW equation of state[J].Chinese Journal of High Pressure Physics,1999,13（1）:55-58.