一种变步长最小均方算法

王才能，裴承鸣，刘东来，王怀文

(西北工业大学动力与能源学院，西安710072)

1 引言

自适应滤波在没有先验知识的情况下具有跟踪输入统计量随时间变化的能力，是信号与信息处理的一个重要手段。在系统辨识、自适应控制、通信、声纳和雷达等技术领域均已得到成功运用。1960年，Widrow和Hoff提出了计算简单、稳定性好、易于实现的最小均方算法(LMS)，随即就成为应用最为广泛的自适应滤波算法。LMS算法基于最速下降原理，将随机梯度用瞬时梯度代替，沿着权值梯度的负方向达到最优权值，实现均方误差最小。自适应滤波器的原理见图1，计算公式为:

其中，d(n)是期望信号，X(n)是输入信号矢量，W(n)是滤波器的权值矢量，e(n)是误差，μ是收敛步长参数。

最小均方算法虽然有着显著的优点，但在收敛速度和稳态误差的兼顾方面却存在难以调和的问题。收敛步长的增加可以改善收敛速度，但稳态误差也随之增大。若为减小稳态误差而减小收敛步长，则收敛速度会降低。为解决这一矛盾，人们提出了很多改进形式，变步长最小均方算法便是其中具有代表性的一类。文献［1］提出了使变步长参数μ正比于误差e(n)，但性能并不理想。文献［2］给出了一种称为S函数的变步长LMS算法(SVSLMS)，其步长调整原则是:在初始收敛阶段或未知系统参数发生变化时，步长比较大，以便保持较快的收敛速度和对时变系统的跟踪速度;在算法趋于收敛后，无论输入噪声如何变化，都应采用较小的步长以获得更小的稳态误差。但在误差接近零时，这种算法的步长变化剧烈，可能导致稳态误差增大。为此，文献［3］对SVSLMS做了进一步的改进。文献［4－6］则分别基于箕舌线、双曲正切函数和反正切函数提出了相应的变步长LMS算法，在一定程度上缓解了收敛速度和稳态误差之间的矛盾。

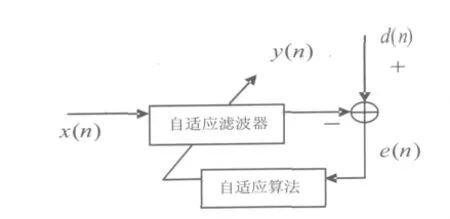
图1 自适应滤波器的原理

2 变步长最小均方算法

现有的一些变步长LMS算法(文献［2－6］所提算法)在处理补偿与误差的关系方面采用了非线性函数，而这些函数的共同特点包括:偶函数、有界(自变量趋于无穷时，函数值为常数;自变量为零时，函数值为零)、是增函数(自变量非负时)。

在对已有算法研究和分析的基础上，下面提出一种新的变步长算法，具体原理如下:

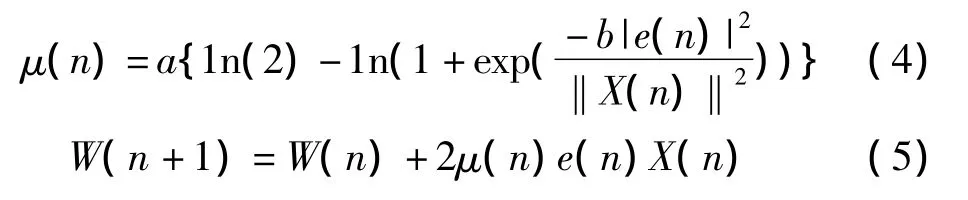
其中，f(z)=a{1n(2)－1n(1+exp(－bz))}是一个有界非线性函数，其随参数a和b的变化特性分别见图 2、图 3。当 Z→∞ 时，f(z)→a1n2≈0.6391a，这样保证了步长在一定范围内变化，不会导致结果发散。当a，b不变时，步长随着误差的增加而增加，符合文献［2］提出的变步长原则。输入信号反映了当前的信息，把它引入到变步长中可提高算法的跟踪性能。

为满足最小均方算法的稳定条件:1＜μ＜1/λmax，要求 1 ＜ μ(n)＜1/λmax，则有 1/1n2 ＜ a ＜λmax×1n2，。当 a增大，步长会增大，收敛速度加快，稳态误差减小。a的具体值需要在实验中确定。参数b用来调整变步长函数的形状以此来控制步长变化的速度。

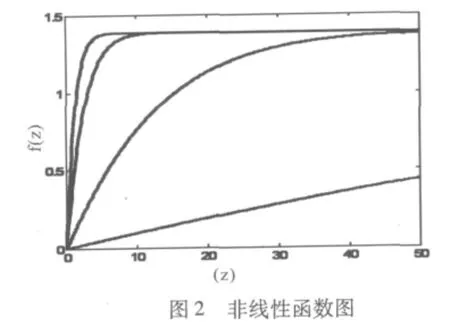
(a=2，从下到上 b=0.01，b=0.1，b=0.5，b=1)

(b=0.3，从下到上 a=0.05，a=0.1，a=0.5，a=1)

3 计算机仿真实验

考虑AR过程u(n)，其差分方程为:

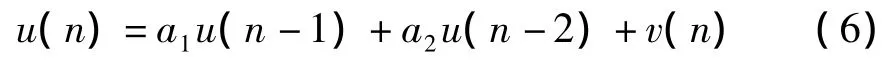
其中，a1= －0.1，a2=0.8。v(n)是均值为零，方差为0.27的加性白噪声。

采用二阶线性自适应预测器来估计AR参数a1，a2。采样点数为500个，为了提高统计置信度共进行100次独立实验。

图4是分别采用上面的新算法(a=0.15，b=0.7)与固定步长(μ=0.025)LMS算法得到的 AR参数变化曲线。可以看出，新算法的收敛速度快，稳态误差小。

图5是分别采用上面的新算法(a=0.15，b=0.7)与文献［3］提出的变步长LMS算法(α=1，β=0.05)得到的AR参数变化曲线。可以看出，新算法在收敛速和稳态误差等性能方面均优于文献［3］算法。

4 结束语

在研究多种变步长LMS算法的基础上，通过引入非线性函数提出了一种新的变步长LMS算法。分析了参数的选取方法，并借助计算机仿真和对比试验验证了新算法的主要性能。为对于收敛速度和稳态误差均要求较高的自适应建模和跟踪控制提供了一种新的计算方法。

［1］Yasukawa H，Shimada S，Furukrawa I，et al.Acoustic echo canceller with high speech quality［C］//IEEE ICASSP，1987:2125－2128.

［2］覃景繁，欧阳景正.一种新的变步长LMS自适应滤波算法［J］.据采集与处理，1997，12(3):171 －174.

［3］高鹰，谢胜利.一种变步长LMS自适应滤波算法及分析［J］.电子学报，2001，29(8):1094 －1097.

［4］邓江波，侯新国，吴正国.箕舌线的变步长LMS自适应算法［J］.采集与处理，2004，19(3):282 －285.

［5］郑莎莎.智能天线变步长最小均方算法的研究与仿真［D］.长春:吉林大学，2007.

［6］朱斌，马艳.一种新的变步长LMS算法分析［J］.计算机仿真，2008，25(9):93 －95，154.