归纳、猜想及证明等差数列前n项平方和公式

陈 达

山东省常乐二中，山东潍坊 262400

归纳、猜想及证明等差数列前n项平方和公式

陈 达

山东省常乐二中，山东潍坊 262400

在不少题目中，当遇到有关“等差数列前n项平方和”的相关问题时，求解很麻烦，大家都很希望有一个解此问题的易理解的固定公式，因此笔者运用 “归纳推理法”加之“数学归纳法”证明推导了“等差数列前n项平方和”公式。

归纳推理；数学归纳法；等差数列；平方和；公式

本文所述内容是根据笔者归纳猜想证明出了“等差数列前n项平方和”公式，即：

1 想法的由来

2 规律的发现与归纳

写出几个等差数列中的几项，通过计算得，这两个值并不是总相等，只有n=1或d=0时才相等且=中位数的平方乘以其个数+R 。并且可断定R定可以写成dm(nk− 1 )的形式，笔者写了一列式子（n≥4，∵n≤3时很难发现其规律）通过他们之间的规律进行了归纳猜想

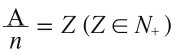
3 猜想及表达

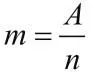
且每组的m1有一定规律：

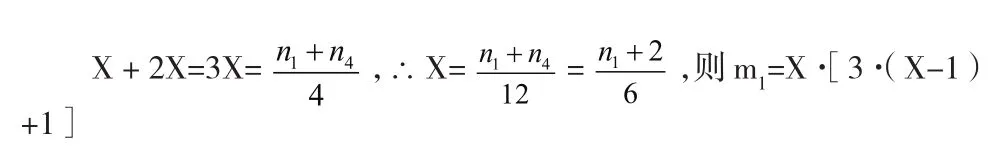
根据这一点猜想归纳出n≥4时求的思路方法步骤进而写出其整体表达式。

思路方法步骤：

1）求项数，之后求出与其项数相连的四个项数n1、n2n3n4，且n1、n4必为偶数 ，n2、n3必为奇数。

3）表示：项数分为4种情况：

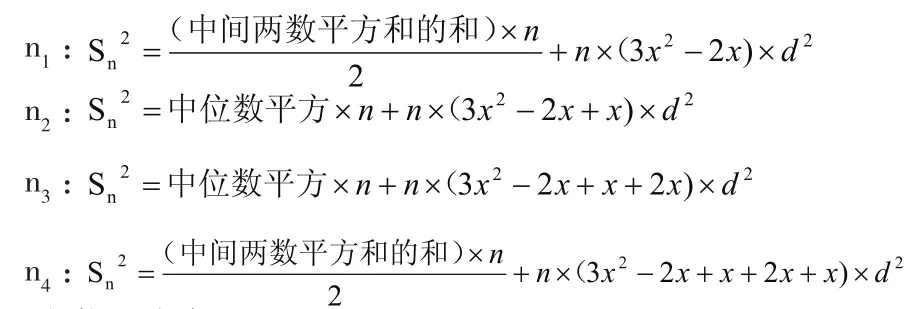
4）推理公式：

观察上面4种情况的最后结果可得都符合一个通式，即：

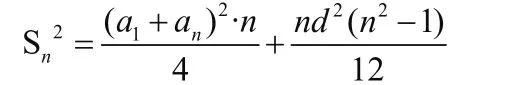
其中n为项数（n≠3Z，，且n≥4，n∈N+），d为公差。另外考虑当n=3Z或n≤3， n∈N+时等式是否成立，为了验证是否在n=3Z或n≤3， n∈N+时等式也成立，我随便举几个例子，看看例子是否成立，如果例子成立，我再进行证明即可。

举例：1）当n=3时，不妨设数列为{1、2、3}，则左边=12+22+32=14

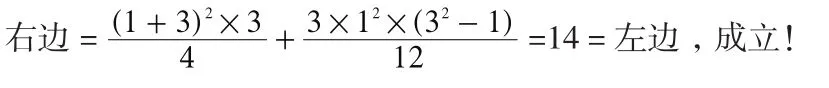
2）当n=6时，不妨设数列为{1、2、3、4、5、6}则左边=12+22+32+42+52+62=91

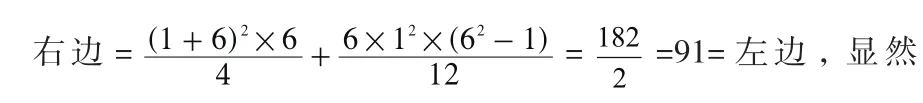
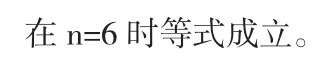
由上面的举例可以看出，在n=3、6时都成立，于是笔者猜想n=3Z或n≤3， n∈N+时等式也成立。通过这些规律等式我大胆的提出一个结论：等差数列前n项平方和公式：

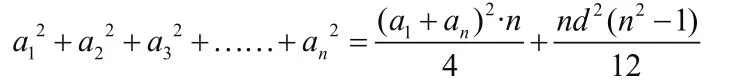
4 “数学归纳法“证明

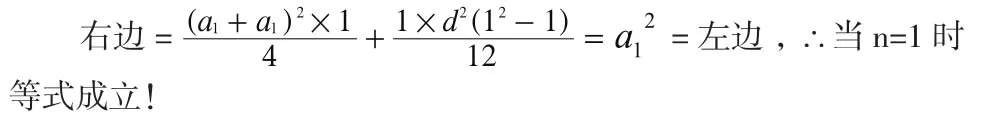
2）假设当n=x时，等式成立。（x≥1，x ∈N+）

∴n=x+1时公式成立

综上所述，对任意正整数，公式恒成立，即等差数列前n项平方和公式：

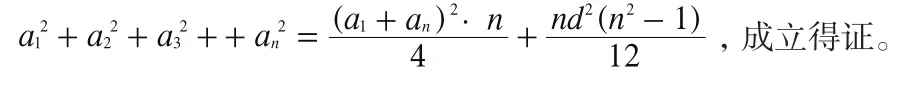
[1]人教B版.高中《数学必修5》之“数列”知识点.

[2]人教B版.高中《数学选修2-1》之“推理与证明”知识点以及“数学归纳法”知识点.

O13

A

1674-6708（2010）30-0164-02

陈达，学生，所在学校：山东省常乐二中