埋地管道、箱涵抗浮计算分析

韩月波，张丽囡

（1.天津市水利勘测设计院，天津 300204；2.天津市水利基建管理处，天津 300204）

近年来，埋地管道、箱涵输水已经成为城市引水、供水工程的首选方式。如，为20世纪80年代建设至今仍为天津市人民造福的引滦入津工程配套的引滦入港、入开发区、入聚酯等供水工程采用的是埋地管道，南水北调中线一期工程天津干线段采用的是埋地箱涵，为南水北调中线一期工程天津干线配套的各条供水线路也将采用埋地管道。埋地管道及埋地箱涵具有保护水质、减少永久占用耕地数量、减少水量损失等明渠供水不可替代的优点。

埋地管道及埋地箱涵的设计中，相关的结构、稳定计算有很多。这里仅以埋地管道为例，就埋地管道及埋地箱涵设计的抗浮计算提出一些看法。

1 埋地管道抗浮计算的目的

埋地管道抗浮计算的目的主要是确定其埋深。埋地管道埋置深度的确定直接影响整个工程的土方开挖及回填量，即影响工程投资。因此，抗浮计算不仅仅是保证工程安全的计算，对工程投资的影响也很大。需要说明的是，管道的埋置深度必须满足抗浮要求，但抗浮计算不是确定其埋深的唯一条件。

2 埋地管道抗浮计算方法

管道的抗浮计算一直被认为是最基本、最简单的计算。凡是搞过管道设计的人应该都很熟悉，实际情况也确是如此。这里，以埋地管道的抗浮计算方法为重点来介绍的原因，是在设计中采用同一个计算公式却出现了两种计算方法，计算结果也有所不同。下面，以壁厚σ为18 mm的DN1800钢管的抗浮计算为例来介绍一下这两种计算方法。

计算条件如图1所示：

2.1 计算公式

计算公式采用 《给水排水工程埋地钢管管道结构设计规程》（CECS 141-2002）中的公式：

式中：∑FGK为各种抗浮作用标准值之和；Ffw，k为浮托力标准值；Kf为抗浮稳定性抗力系数，取Kf＝1.1。

2.2 计算目的

确定满足抗浮要求的管顶最小埋深（H）。

2.3 计算参数

主要计算参数，包括回填土浮容重（γs）＝10 kN、水容重（γw）＝10 kN、钢管容重（γf）＝78.5 kN、钢管外径（D）＝1.82 m、钢管内径（d）＝1.82-0.018×2＝1.784 m。

2.4 计算工况

地下水位至地面高程，管内无水。

2.5 计算方法一

为简化，取1延米管道进行计算。

式中：G土、G管、G水分别为管顶上土重、管材自重和管顶上水重。其计算公式分别为：

管底所受的扬压力计算公式为：

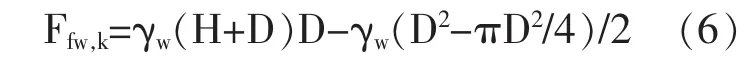
因此，∑FGK＝KfFfw，k可转化为：

经计算，H＝1.28 m。

2.6 计算方法二

为简化，取1延米管道进行计算。

管道所受的浮托力计算方法为：

因此，∑FGK＝KfFfw，k可转化为：

经计算，H＝1.13 m。

3 对两种计算方法的理解

两种计算方法的公式看上去没有太大差别，为什么计算结果却不同呢？我们仔细分析一下这两种计算方法所考虑的受力分析便会明白。

计算方法一考虑的各种抗浮作用（即向下的力）分别为管顶上土重、管材自重和管顶上水重，管道所受的浮托力（即向上的力）为管底所受的扬压力。

计算方法二考虑的向下的力分别为管顶上土重和管材自重，管道所受的向上的力为管道所受的浮托力（该浮托力采用阿基米德定律计算）。

由以上分析可看出，该两种计算方法的区别在于方法二所考虑的水的作用仅为浮托力，浮托力是采用阿基米德定律直接计算得出结果；而方法一所考虑的水的作用是管顶以上的水重和管底的扬压力。其实方法一所考虑的管顶以上的水重和管底的扬压力形成合力后的结果与方法二采用阿基米德定律直接计算得出的结果是相同的，方法一只是将方法二的浮托力分解为向下和向上的两个力。但是，出现最终计算结果不同的原因在于：方法一先将由阿基米德定律计算出的浮托力分解为向上和向下的两个力，然后只是将向上的力乘上了抗浮稳定性抗力系数Kf，而方法二则是将由阿基米德定律计算出的浮托力直接乘以Kf，即相当于将方法一中水的向上和向下的作用均乘了Kf。

搞清了出现不同计算结果的原因后，我们分析一下这两种计算方法的合理性。

这两种计算方法的区别在于方法二是采用阿基米德定律计算浮托力，而方法一则是将阿基米德定律计算的浮托力又分解为向上和向下的两个力。如果没有抗浮稳定性抗力系数Kf，则这两种计算方法的计算结果是相同的，有了Kf以后则采用方法一计算出的允许最小覆土厚度（H）永远比采用方法二计算出的要大。其原因很简单，Kf是个大于1的常数，方法一将方法二中采用阿基米德定律计算出的浮托力F分解为向上的力F1和向下的力F2（F、F1和 F2均为正数），F 是个定值，且 F＝F1－F2，显而易见 KfF＜Kf（F1－F2），KfF 为方法二所需抵抗的浮托力，Kf（F1－F2）则为方法一所需抵抗的浮托力。因此，方法一计算出的允许最小覆土厚度永远比采用方法二计算出的要大。抗浮稳定性抗力系数Kf是个安全系数，工程项目计算中之所以要乘安全系数，是因为有许多不确定因素的存在，而我们的抗浮计算方法一中只给F1乘了安全系数，没给F2乘，相当于将F2也视为不确定因素，而实际上F1和F2的差值是个定值，是可以确定的，因此方法二是比较合理的。假设某工程需要一个1 m3的立方体实心铁块放在 1 000 m深的γw＝10 kN的淡水下，采用方法一和方法二来计算一下它的抗浮，方法一的计算结果是Kf=1.006 85，不满足抗浮稳定要求，若要满足Kf≥1.1的要求还需对铁块施加一个大于或等于931.5 kN的向下的力；而方法二的计算结果则是 Kf＝7.85，7.85 远远大于 1.1， 满足抗浮稳定要求。这个例子虽然有些极端，但是不难想象，实心铁块放在γw＝10 kN的淡水中是不可能浮起来的，无论放在多深的水中其抗浮稳定也应是安全的，从而可以判断出计算方法一是不合理的、方法二是合理的。

4 抗浮计算方法的选择对埋地管道、箱涵工程的影响

如前所述，管涵的抗浮计算影响其埋置深度，进而影响工程投资。那么选择上述两种不同的计算方法会对管涵的埋置深度有多大影响呢？这里以不同公称直径的钢管在一般地段铺设和DN1800钢管穿越不同水深的河道为例来分析一下。

4.1 不同公称直径的钢管在一般地段铺设

不同公称直径的钢管其壁厚均取其公称直径的1%，选取公称直径DN1000—DN3000钢管进行计算，采用两种计算方法计算的满足抗浮稳定要求的允许最小埋置深度见表1：

表1 不同管径钢管在一般地段铺设允许最小埋置深度计算结果

由表1可知，采用两种计算方法计算的允许最小埋置深度差值随着管径的增加而增加。

4.2 DN1800钢管穿越不同水深的河道

DN1800钢管壁厚采用0.018 m，选取河道深度为1～11 m进行计算，采用两种计算方法计算的满足抗浮稳定要求的允许最小埋置深度见表2。

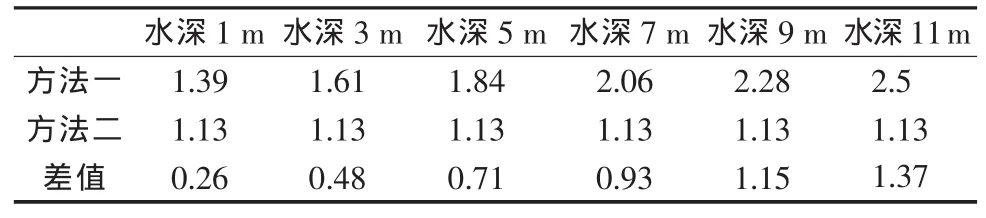
表2 DN1800钢管穿越不同水深河道允许最小埋置深度计算结果

由表2可知，DN1800钢管穿越不同水深的河道时采用方法二计算的结果不会因水深的变化而变化，采用方法一计算的结果则随着水深的增加而增加、增加值与水深呈线性关系。

4.3 分析

通过以上两例可看出，采用方法二计算出的管顶覆土厚度都要小于采用方法一计算出的结果，而且随着管径的增大和管顶以上水深的增加，这差值也越来越大，尤其管线穿越河道时河道水深对管顶覆土厚度影响非常明显。管顶覆土厚度的加大必然使土方工程量增加、占地宽度增加，从而增加工程投资，尤其穿越河道时管顶覆土厚度的加大更是增加了施工的难度。以上两例只是以钢管为例，箱涵也是如此，而且箱涵的方形或矩形断面会使这两种计算方法的差别更明显。因此，抗浮计算方法的选择对埋地管道、箱涵工程的影响还是很大的。

5 结语

在工程设计中，应根据工程实际情况，选择正确合理的抗浮稳定计算方法，再综合其他因素，合理地确定管涵的埋置深度，使工程在满足安全性、适用性的基础上尽量减小投资，以最小的代价造福人民。