降落伞“呼吸”现象研究
郭叔伟 王海涛 董杨彪 秦子增
(国防科技大学航天与材料工程学院,长沙410073)
1 引言
降落伞“呼吸”现象是指在降落伞第一次充满后,伞衣投影面积在一定范围内上下波动,表现为伞衣像呼吸一样以一定周期一张一缩的变化。在国内外空投试验、风洞实验、实际航天器返回中多次发现降落伞“呼吸”现象,如美国的“海盗VIKING”号飞船在试验飞行中有降落伞“呼吸”现象的详细记录[1];国内余莉等人在降落伞风洞实验中也多次发现降落伞“呼吸”现象,且发现在风洞试验条件下降落伞“呼吸”现象特性与伞衣和连接带的材料有关[2-3];在某型号飞行器空投试验中通过图像处理也多次发现其主伞在首次充满后存在比较明显的“呼吸”现象。
降落伞“呼吸”现象首先表现是伞衣第一次充满后,伞衣继续向外扩张充气,导致降落伞阻力面积峰值大于设计的全充满阻力面积,使开伞充气过程中最大开伞力预测精度降低。在降落伞“呼吸”现象发生后,由于伞衣面积产生周期性波动,由此带来物伞系统“喘振”,以及降落伞伞绳和吊带受力周期性波动,进而有可能导致共振发生。
在国内外有关降落伞“呼吸”现象的理论研究文献比较少,大部分有关降落伞“呼吸”现象的文献只是描述“呼吸”现象的产生以及特征。在已有的研究方法中主要有两类:1)流固耦合理论计算,分别建立伞衣流场模型,伞衣应力分析[4],国内以彭勇为代表建立了降落伞充气过程中伞衣伞绳弹簧阻尼模型[5];2)商业软件计算,主要是通过LS-DYNA等商业软件计算降落伞充气过程[6]。以上两种方法其建模过程相当复杂,且带来了一系列需要经验和实验确定的参数,这给降落伞设计单位和相关工程单位带来不便。本文以简化的降落伞充气过程中轴向和径向动量方程为基础,考虑伞绳弹性,给出比较简单的降落伞“呼吸”现象计算方法。
2 降落伞充气模型
在降落伞充气过程中,一般把降落伞充气过程分为两个阶段:初始充气阶段和主充气阶段。初始充气阶段是从空气进入伞衣开始直到空气充至伞衣顶部为止;主充气阶段是完成已充气部分继续膨胀,直到伞衣完全充满,在这过程中降落伞的形状用一个半径为r的半球和一个倒截锥的组合体来表示,伞绳长度为Ls,如图1所示。图中D0为降落伞名义直径;θ为伞绳与降落伞对称轴的夹角。
为了建立方程,首先在充气过程中做如下假设:
1)降落伞简化为轴对称模型;
2)平面大地;
3)载荷物和降落伞轴向速度一致,且垂直下落;
4)伞衣阻力系数不变;
5)大气密度不变;
6)完全充满后,伞衣为半球形,半径为r0。
在主充气阶段,对载荷物和未充气伞衣部分作轴向动量方程:
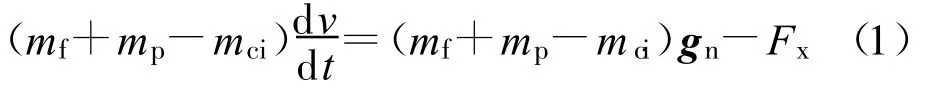

图1 伞衣在主充气过程中的形状
对已充气伞衣和伞衣附加质量作轴向动量方程:

方程(1)、(2)中mf为载荷物质量;mp为降落伞的质量;mci为已充气部分的伞衣质量;v为物伞系统的瞬时轴向速度;Fx为轴向力;mx为降落伞轴向附加质量;qc为动压;Cx为降落伞轴向阻力系数,一般通过风洞实验和空投试验得出;Sc为伞衣投影面积。
对已充气伞衣和伞衣附加质量作径向动量方程:
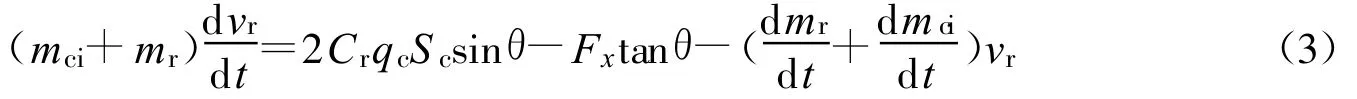
方程(3)中mr为径向附加质量;vr为伞衣瞬时径向速度;Cr为降落伞径向扩张力系数;θ为伞绳与降落伞轴线的夹角。vr可用伞衣瞬时投影半径 r表示:

方程(1)~(4)即为降落伞主充气过程的动力学方程,要解这四个方程还需要得到 mc、mx、mr、Sc、Cr的值和一些初始条件。
降落伞伞衣已充气部分为图1中半径为r的半球的那部分伞衣,因此有:

式中mc为伞衣质量。根据相关文献[7,8]有:

式(6)、(7)中ρ为大气密度。
伞衣投影面积Sc为:

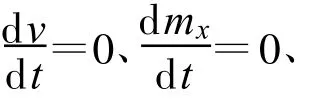

当伞衣半径r>r0时,假定 Cr=0。
伞绳与降落伞轴线的夹角θ为:

考虑伞绳弹性变化,式(10)中Ls也是变化的,对伞绳节点有平衡方程:
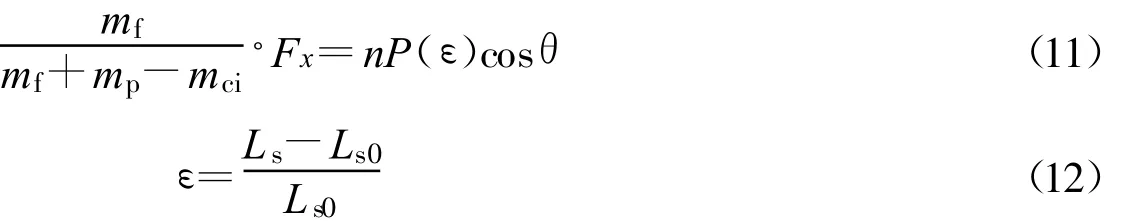
式(11)、(12)中n为伞绳根数;P(ε)为单根伞绳张力P随其应变ε的变化关系;Ls0为伞绳原长。由Fx和r代入方程(10)、(11)、(12)通过迭代得到Ls和 θ。对于线弹簧模型伞绳材料 nP(ε)可简化为:

式中K为弹性系数。
对于一级充气阶段的降落伞,其伞衣投影半径r的初始值可取初始充气时末期的伞衣投影半径r1和初始充气时间t1[5]:

式(14)、(15)中vL为伞衣拉直时系统速度;λ为初始充气参数,对于平面圆实伞[5],λ≈1.73。对于解除收口阶段的降落伞,其伞衣投影半径r的初始值可取收口伞衣半径。物伞系统的瞬时轴向速度v的初始值为vL,Fx和vr的初始值可取为0。把初始条件代入方程(1)、(2)、(3)、(4)进行积分即可得到降落伞充气过程伞衣和伞绳力变化过程。
3 计算结果分析
本文选定伞衣直径为8.53m的美国C-9伞[9]为对象,研究不同开伞速度、载荷物质量、大气密度、伞绳弹性系数等参数对降落伞“呼吸”现象的影响。工况设置如表1所示。其中工况1与文献[10]的试验条件一致,通过计算该工况的充气时间来验证数学模型的正确性,也为其他试验工况的仿真结果提供比较对象。

表1 计算工况
在工况1的计算结果中,包括初始充气的时间在内的降落伞第一次充满的时间约为0.96s,文献[10]试验值为0.93s。根据文献[9]中计算充气时间的经验公式:

式中Kc为充气常数。C-9型伞的Kc值一般在8~10之间[11],本文模型计算得到的结果对应值为8.44。本文模型计算得到的结果与实验结果基本吻合,充气常数在经验公式的大致范围内,由此可见本文的充气过程计算模型是可行的。
工况1充气过程中伞衣半径变化和伞绳力如图2,3所示。图2中伞衣半径变化规律基本与文献[2]的实验现象类似。

图2 工况1充气过程伞衣半径变化

图3 工况1充气过程伞绳拉力
在工况1的基础上,分别增大开伞速度、减小载荷物质量、增大开伞大气密度、减小伞绳弹性系数得到不同工况下伞衣半径变化如图4、5、6、7所示。

图4 不同开伞速度下伞衣半径变化

图5 不同载荷质量下伞衣半径变化

图6 不同大气密度下伞衣半径变化
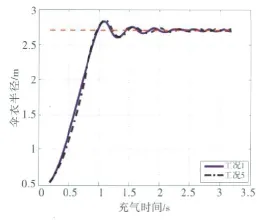
图7 不同伞绳弹性系统下伞衣半径变化
从图4中可以看出,增大开伞速度、充气时间缩短,但充满后伞衣半径变化规律基本不变;从图5中可以看出,减少载荷物质量,伞衣“呼吸”频率降低,上下变化幅度增大;增大大气密度与减少载荷质量的变化情况相类似,如图6所示;从图7中可以看出小范围内改变伞绳的弹性系数变化几乎不影响伞衣“呼吸”现象,这与文献[2]的实验现象类似。从降落伞径向动量方程(3)可知,伞衣半径的变化主要取决于伞绳力和伞衣径向扩张力,而充气过程中、特别是刚充满后系统速度已经接近物伞系统平衡速度时,伞绳力和伞衣径向扩张力一般由载荷物质量、大气密度所决定,此时降落伞“呼吸”现象很大程度上取决于载荷物质量和大气密度,当载荷物质量较小和大气密度较大时,降落伞“呼吸”振荡幅度较大且不易衰减。
4 结论
降落伞“呼吸”现象广泛存在于降落伞充气过程中,一般情况下,在充满后一定时间内,降落伞伞衣半径的振动会逐渐衰减,但也有一些型号的降落伞会产生自激振荡,其伞衣振动一直保持一定的周期和幅度[4]。降落伞“呼吸”现象一般会影响最大伞绳力以及充满后的物伞系统稳定性。本文通过建立简化的非收口型降落伞充气过程中轴向和径向动量方程,基本描述了降落伞充满后伞衣“呼吸”过程,其计算得到的结果与空投试验和风洞试验数据基本吻合。通过数学模型和计算分析发现,在有限质量充气时,尤其是在降落伞刚充满物伞系统就接近稳定平衡速度,降落伞伞衣径向变化主要取决于载荷物质量和大气密度,当载荷物质量较小和大气密度较大时,降落伞“呼吸”振荡幅度较大且不易衰减。在本文的数学模型中没有考虑收口型降落伞中降落伞环向力,也没有考虑降落伞充满后伞衣径向扩张系数,在实际空投试验中发现,在开伞动压较大时,尤其是降落伞充满时刻的动压较大时,充满后伞衣径向扩张系数不可忽略,下一步可开展收口型降落伞和考虑降落伞充满后伞衣径向扩张系数的相关方面研究。
[1]Wbitlock C H,Poole L R,Talay T A.Postflight simulation of parachute deployment dynamics of viking qualification flight tests[R].NASA-TD-D-7415.1973.
[2]余莉,李水生,明晓.降落伞弹性现象对伞衣载荷的影响[J].宇航学报,2008,29(1):375-379.
[3]余莉,明晓,胡斌.降落伞开伞过程的试验研究[J].南京航空航天大学学报,2006,38(2):176-180.
[4]Roberts B W.Axi-symmetric self-excited oscillations in parachutes[R].AIAA 73-452.1973.
[5]彭勇.载人飞船回收系统若干动力学问题的研究与应用[D].长沙:国防科技大学博士学位论文,2004.
[6]Tutt B A,Taylor A P.The use of LS-DYNA to simulate the inflation of parachute canopy[R].AIAA 2005-1608.2005.
[7]程文科.一般降落伞-载荷系统动力学及其稳定性分析[D].长沙:国防科技大学博士学位论文,2000.
[8]王利荣.降落伞理论与应用[M].北京:宇航出版社,1997.
[9]Ewing E G,Knacke T W,Bixby H W.回收系统设计指南[M].吴天爵,马宏林,吴剑萍,等译.北京:航空工业出版社,1988.
[10]Heinrich H G,Saari D P.Parachute opening shock calculations with experimental established input functions[J].Aircraft,1978,15(2):100-105.
[11]《降落伞技术导论》编写组.降落伞技术导论[M].北京:国防工业出版社,1977.

