降落伞充气过程中伞衣外形及流场变化研究
张红英,刘卫华,秦福德,童明波
(南京航空航天大学航空宇航学院,江苏 南京 210016)
0 引言
在降落伞拉直、充气及稳定下降等一系列动作中,充气过程是影响其安全稳定性最为关键的环节,也是物理过程中最复杂的一个过程,因而成为了当前降落伞研究领域的热点及难点问题之一。在对降落伞开伞过程的分析中,传统上主要依靠试验研究,但由于充气时间一般很短,有时不到半秒就完成了充气过程,导致在这样的一个动态充气过程中试验状态的模拟和各项参数的记录非常困难。因此降落伞的风洞试验研究一般偏重在开伞载荷与气动力系数的研究上[1-4]。而事实上,由于降落伞是个柔性织物透气体,它在开伞过程中经历了急剧的结构大变形,因而伞衣内外的流场十分复杂,只有深刻地了解降落伞周围的流场,才能深刻理解降落伞工作时的工作机理,也才能更好地从理论上解决我们关心的问题,解释伞衣充气时的诸多气动力现象。这就必须依靠充气过程的动态数值模拟来获得伞衣形状变化和流场变化之间的关系,从而提高降落伞的理论分析水平。
随着计算机技术的发展和数值模拟技术精确度的提高,同时降落伞设计、研制所要求的周期缩短及日益高涨的试验费用,近年来,已有不少研究人员发表了论文,探讨如何采用计算流体力学(Computational Fluid Dynamics,CFD)方法来模拟降落伞开伞过程[5-10]。这些研究论文已见报道并给了我们很多启示。但同时我们也发现,这些计算模型都不能模拟降落伞从任意初始形状迅速展开直到完全充满,即不能对降落伞初始充气阶段的开伞过程进行模拟。在文献中,一些研究者使用了充分膨胀的形状作为最初形状[7,10];另一些研究者使用了轴对称的假定来进行近似计算[5-6,8];有的甚至仅考虑稳定状态的情况[9,11]。为此,本文以平面圆形伞为原型,对轴对称降落伞整个充气阶段的流场进行了数值模拟和分析,以详细了解降落伞整个开伞过程中伞衣外形变化及伞衣内外流场的变化情况。
1 充气过程数学模型
1.1 结构动力学模型
本文以平面圆形伞为原型建立模型,对降落伞模型作如下假设:
1)忽略质点的重力影响,径向加强带的充气过程是轴对称的;
2)伞绳、加强带和伞衣是弹性体,符合虎克定律。
降落伞伞衣由一定数量的相同伞衣幅彼此缝合连接而成,相邻伞衣幅之间由加强带相连。在对称充气情况下,选取两对称径向加强带来表示伞衣充气过程的形状变化,将研究对象(一根加强带和两边的两个半幅伞衣)离散为一系列用阻尼弹簧连接的质点,分布在加强带上。质点与质点之间的受力示意图如图1所示,其中FP为伞衣质点受到的气动压力,α为气动力与Y轴的夹角,Ti、Ti-1分别为i与i+1质点、i与i-1质点之间的弹性力和阻尼力之和,β为伞衣质点之间的张力和X轴的夹角,Fz为伞衣织物(收口绳、伞顶孔加强带)纬向张力在伞坐标X轴方向上的分力(当两加强带之间的距离大于伞衣幅的宽度时才存在)。根据牛顿运动定律,伞衣各质点的结构动力学方程为:
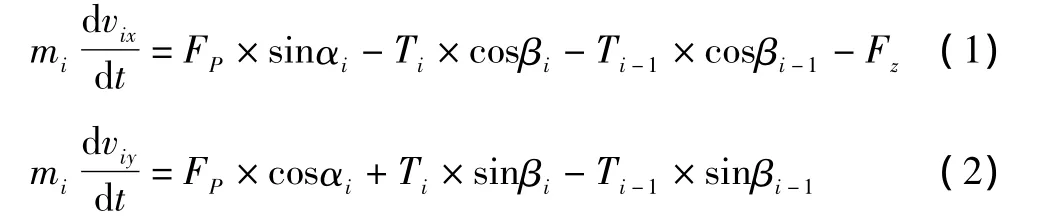

图1 质点间受力示意图Fig.1 Force diagram of the free body of canopy
1.2 计算流体力学模型
降落伞伞衣的厚度很小,远小于伞衣的几何尺度。因此从流体力学的角度来考虑,可以把伞衣看成是薄膜材料,其厚度对流场本质不会产生影响,在对降落伞进行流体力学数值模拟时可以忽略伞衣厚度的影响。采用准定常假设,把充气过程中的降落伞视为刚体,通过对不同充气时刻的不同伞衣外形进行不可压Navier-Stokes(N-S)方程求解来模拟降落伞的流场特性。选用二维雷诺平均N-S方程作为控制方程,采用有限体积结构网格数值格式进行流场模拟。

二维守恒型雷诺平均Navier-Stokes方程可写为:式中:W为守恒通量,Re为雷诺数,E、F为对流通量,Ev,Fv为粘性通量。
在这基础上对结构模型和流场模型进行耦合计算:先根据初始数据,在每一时间步长开始时,降落伞到达一个新位置,将伞面附近的流场网格点移动至伞面上;通过修改这些点相应的动量方程,更新源项,利用CFD程序计算得出交界处质点的压差,将计算结果传给结构动力学方程,进行表面力计算和进行伞面变形运动计算,得到下一形状,依据下一形状,流场计算程序进入下一个时间步长,开始新一轮的计算。
织物的透气性是指在织物的两侧存在空气压力差时,空气从织物的孔隙透过的性能。本文引用了多孔介质(Porous jump)边界条件,并以602锦丝66绸为例进行计算模型验证。Porous jump边界条件是对多孔介质模型(porous media model)的一维简化,用于模拟流场中已知“压力损失-透气速度”关系的“膜”。该边界条件的“压力损失-透气速度”关系由以下公式给定:其中μ是流体粘性系数,ρ为流体密度,α是介质的透气系数,C2是压力跃变系数,v是垂直于介质表面的速度大小,△m是介质厚度。α、C2和△m是Porous jump边界条件中需要设置的参数。

从公式(4)中可见,将压力损失△p表示为透气速度v的二次函数。在实际计算中,流体粘性系数μ、流体密度ρ和介质厚度△m为已知量,还有α和C2两个参数需要确定。如果已知一组透气速度和压力损失的实验数据,则可以通过对实验数据进行二次多项式插值的方法确定α和C2两个参数。下面以602锦丝66绸为例说明α和C2的确定过程。
表1为602锦丝66绸透气速度与压力损失的一组实验数据[12],采用过原点的二次多项式对这组数据进行拟合(如图2所示)可得:
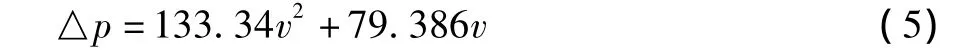
比较式(5)和式(4),由对应常数项相等可得:

标准大气条件下空气密度ρ为1.225kg/m3,粘性系数μ为1.726×106kg/ms,设介质厚度△m为0.0005m,则由以上两式计算可得:


表1 不同透气速度下压力损失的计算值与实验值[12]对比Table1 The comparison of calculated and experimental values [12] of air speed and pressure loss
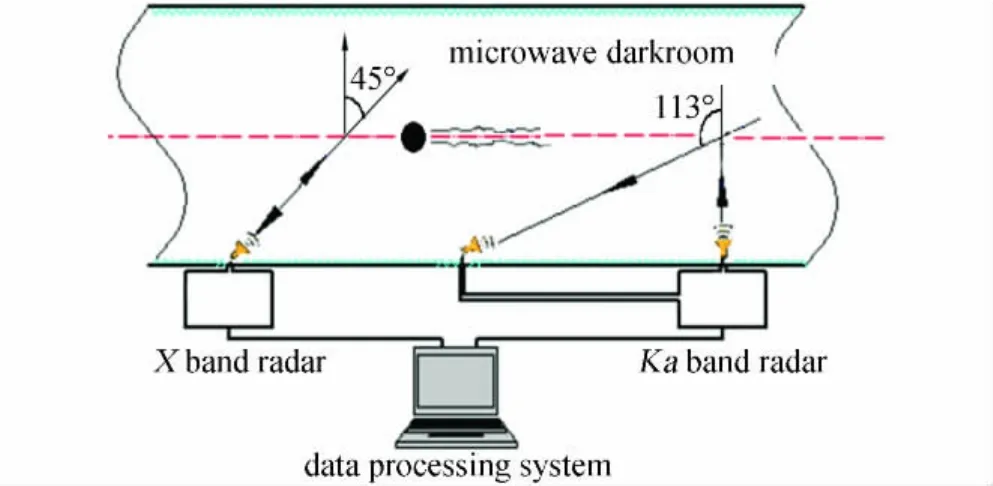
图2 二次多项式曲线拟合结果Fig.2 Quadratic polynomial curve fitting results
为了验证采用Porous jump边界条件模拟降落伞伞衣透气性的可靠性,制作了一个如图3所示的计算模型。该模型的计算域为二维长方形“通道”,侧边指定为周期边界,Porous jump边界设置在“通道”中间位置,相当于在通道中间加了一层“透气膜”,在速度入口指定空气流速,压力出口设置为标准大气压。对该模型进行计算直至收敛后,可以得到入口和出口之间的压力差,此压力差即为Porous jump边界模拟的“透气膜”在当前流速(即透气速度)下的压力损失。根据之前对602锦丝66绸透气参数的计算,设定Porous jump边界的参数为:△m=0.0005m,C2=435395.9,α =1.1270×10-10。将速度入口的空气流速分别设定为表1中的速度,即可计算得到相应的压力损失,结果如表1所示。从表1可看出计算值与实验值的结果比较接近。本文的伞衣材料为411平纹绸,也可使用该方法模拟其透气性。

图3 透气性验证计算模型的边界条件和网格示意图Fig.3 Boundary condition and grids schematic for porosity verification calculation
2 试验装置及测试系统
充气时间一般很短 ,有时不到半秒就完成了充气过程,在如此短的时间内,伞衣发生了剧烈的变形,伞衣周围流场变化十分复杂,在这样的一个动态充气过程中试验状态的模拟和各项参数的记录非常困难。因此只对降落伞充满时的绕流流场进行了定量测量,将该状态的测量结果和计算结果进行对比分析,以检测计算结果的可靠性。
试验是在南京航空航天大学的非定常回流低速风洞进行的,降落伞在风洞中的照片如图4所示。该风洞是国内首座非定常风洞,通过水平并列旁路加上非定常流动控制机构实现试验段的非定常流场,在作为定常风洞使用时具有低湍流度,低噪声的特点。实验段开口为1.5m×1m的矩形,全长1.7m,紊流度小于0.05%,最大风速是40 m/s,最低稳定风速为0.5m/s。

图4 降落伞在风洞中的照片Fig.4 Experimental apparatus
降落伞的内外流场十分复杂,气流有较大的偏角,因此采用七孔探针来测量其周围的流场,七孔探头的结构如图5所示。七孔探针可以得到流场中的三维速度及压力信息,对气流偏角为78°的大偏角流动,其测试精度为1%[9]。为提高测量效率,利用多根七孔探头制成耙,可以同时测量空间多个点的气动参数。气孔探针在试验前需要进行校准,由于气孔探针的校准系数较多,实际试验中七孔探针将流场中局部点的七个孔压力值由多通道微压变送测试仪转换成模拟电压量,经高精度采集模块将电压量转换成数字量。经过计算机采集后按校准试验得到的系数运算得到速度向量,局部总压、静压值等测量结果。整个测试系统的配置如图6所示。

图5 七孔探头的结构Fig.5 Seven-hole probe

图6 测试系统配置图Fig.6 Testing system
本试验采用有伞顶空的平面圆形伞,其物理参数为:伞衣副数为8块,伞顶孔直径为100 mm,伞衣直径为600mm。伞绳长465 mm,材料为3.2-120锦丝绳,其弹性模数为4000 N。伞衣名义面积为0.32m2,材料为411平纹绸,弹性模数为30000N/m。
3 结果分析
3.1 充气过程伞衣外形变化及流场变化
计算模型与试验用伞的物理模型一致,采用以第1节所介绍的数学模型对该模型进行了整个充气阶段的数值模拟,计算的初始状态与实验状态一致,气流来流速度为20m/s。通过计算,得到了伞衣外形变化和伞衣周围的流场变化。
初始充气阶段是气流从伞衣底部冲到伞顶的阶段,图7为初始充气阶段的伞衣外形变化及流场变化图。图7(a)为气流刚进入伞衣口时的状态,从图中可看出,外扩状“喇叭口”导致大的分离区,在“喇叭口”之后产生较大面积的局部低压,该区域伞衣内外压差较大,达到1.6左右,促进伞衣口迅速膨胀扩张。图7(b)所示的状态中,伞衣口外形扩张为“口杯”状,流动分离区紧贴伞衣外表面,相比状态7(a)明显变窄,分离区伞衣的内外压差除紧邻伞衣底边的小区域外,总体上小于状态7(a)的情况,伞衣内存在涡流,但流速极低,基本不影响伞衣内滞止压力的大小。图7(c)所示的状态中,气流在伞衣内形成一对方向相反的漩涡。伞衣呈先扩后收的形状,伞衣外基本为附壁流动。扩张部分伞衣向外排挤气流,使气流加速,伞衣外表面压力降低,伞衣内外压差系数在1.5左右。收缩部分气流减速,伞衣外表面压力逐渐恢复至大气压,伞衣内外压差随之逐渐减小。图7(d)所示的状态为伞顶孔完全冲开时的状态,此时气流从伞衣底边流入,再从伞顶孔流出,没有发生流动分离,可见伞衣的结构透气性对流场会产生显著影响。从压力等值线图来看,伞衣内的滞止压力系数在顶端开口和伞衣透气的条件下仍然达到最高0.85左右,伞衣外表面的压力系数则因为平滑的伞衣外形和伞衣透气性的影响降低到仅有-0.15左右。说明伞衣的透气性对伞衣内滞止压力的影响较小,对伞衣外流场结构的影响较大,从而对伞衣外表面的压力影响较大。

图7 初始充气阶段的伞衣外形变化及流场变化图Fig.7 Canopy shape and flow-field vs.time in the initial inflation phase
图8为主充气阶段的伞衣外形变化及流场变化图。图8(a)所示的状态为主伞主充气阶段的初期,可以看出伞顶孔张开至更大,气流在伞衣内的滞止有所减弱,且由于伞衣织物透气的作用,气流滞止过程从伞衣口至伞衣顶持续进行,伞衣内部压力系数从伞衣口附近的0.76增加至伞衣顶附近的0.9以上。尽管伞衣外形在气流方向前大后小,由于伞衣织物透气的作用,伞衣外表面仍没有发生明显的气流分离。伞衣尾部由于有伞顶孔“射流”的存在,也没有发生明显的流动分离。伞衣外表面压力除伞衣口附近局部较低外,其余部分压力接近大气压,伞衣尾部压力也很快恢复至大气压。
图8(b)所示的状态中伞顶孔面积张至最大,空气首先在伞衣顶部聚集,使伞衣顶部膨胀。没有明显的流动分离发生,伞衣内部流动滞止效应进一步减弱,压力系数为0.74。与图8(a)中的状态不同的是,由于伞顶孔面积增大,结构透气量增大,伞衣织物透气性对气流在伞衣内滞止的影响相对减弱,伞衣内压力系数从上一个状态的逐渐增大转变为基本不变。另外,由于伞衣直径在尾部有增大,形成局部低压。


图8 主充气阶段的伞衣外形变化及流场变化图(前:压力系数等值线图,后:流线图)Fig.8 Canopy shape and flow-field vs.time in the Inflation Phase
如图8(c)所示,伞衣直径继续扩大,呈直筒状。从图中的流线图可以看出,在伞衣外表面附近流线发生扭曲,但没有形成漩涡,这是伞衣织物透气的影响(如果没有伞衣织物透气性,将会有漩涡形成)。在伞衣尾部仍然没有看到明显的流动分离发生,流线以很大的曲率弯曲绕过伞衣尾部,这一方面是受伞衣透气性的影响,另一方面是伞顶孔射流对周围气流有吸入作用。从压力等值线图来看,伞衣内部压力系数从伞衣口的0.9左右向伞顶方向逐渐增加至0.96以上,逐渐滞止现象再次出现图8(b)所示状态中(该现象不明显),这是因为伞顶孔面积张至最大保持不变以后,随着伞衣的继续扩张,伞衣展开面积增大,伞衣侧面织物透气的面积继续增大,对气流滞止的影响也相对减小。
如图8(d)所示,相对8(c)中的状态,伞衣形状呈长宽比更小一些的直筒状(从伞衣口到伞衣顶稍有扩张)。由于伞衣尾部面积的增大,气流无法再顺滑地绕过而发生分离漩涡。由于主流和伞顶孔射流分别在漩涡区的两侧都沿顺流方向对旋涡区内空气形成强剪切,因此在一个漩涡区内形成两个相反旋转方向的漩涡。从压力等值线来看,漩涡区使得整个伞衣尾部的压力有所降低,该区域压力需要远离伞衣尾部更远的距离才完全恢复至大气压力。
在图8(e)中,伞衣直径继续扩大,伞衣尾部已经呈现圆弧形。漩涡区随着伞衣直径的扩张而增大。主流对漩涡区气流的剪切作用相对伞顶孔射流的剪切作用增大(伞衣直径扩张分离区扩大,则主流对漩涡区的剪切面积增大,而伞顶孔面积不变,其射流的剪切面积也基本不变),因此漩涡区两个漩涡中外侧的一个漩涡变大。从整个漩涡区的尺度来看,已经与伞衣张开的尺度相当。从压力等值线来看,伞衣尾部压力随着旋涡区的增大继续降低,且低压范围也继续扩大。伞衣内部压力仍主要受气流滞止作用影响。由于伞衣开口面积增大,伞衣透气量相对进入伞衣的气流量的比例有所下降,因而伞衣内滞止压力有所上升,达到接近1.0。
在图8(f)中,伞衣完全张满。主流对漩涡区气流的剪切面积更大,主要受主流剪切作用影响的漩涡(单侧的两个漩涡中靠外的一个)一面向外扩大尺度,一面向内挤压伞顶孔射流和另一个漩涡。在伞衣尾流轴线上形成了较长区域的回流,伞顶孔射流的绕行现象更明显,射流和内侧漩涡被挤压至离伞顶更近的区域。从压力等值线来看,伞衣后出现了更大面积的低压区,这是漩涡区扩大的结果。
3.2 计算与试验的对比
图9为试验中三维测量结果在半幅中心面上的流场显示,对比图9(f)中计算所得到的流场可以看出,伞衣前、侧流场结构均相似,从伞衣尾部看,计算场和试验场的截面流线都出现了汇聚,从伞顶及绕伞衣底边流出的流线都会包围中间的紊流旋涡向尾部流去。但由于测量场的测量间距偏大,流场拓扑结构不明显。再对压力场进行比较分析,在图9中显示的是压力,测量压力单位为mmH2O,试验的来流速度是20m/s。图中显示伞衣内最大压力约为240Pa(24.37),换算压力系数约为0.98。而伞衣外部漩涡中心区最低压力约为-95Pa(-9.58 mmH2O),换算压力系数约为-0.4。对比图8(f)中的压力系数,二者误差不大。因此所采用的数学模型是可靠的,能通过其计算来定性分析绕伞衣流动的流场特性。

图9 风洞流场测量结果Fig.9 The experimental flow-field around canopy
4 结论
本文以平面圆形伞为原型,对轴对称降落伞整个充气阶段的流场进行了数值模拟和分析,以详细了解降落伞整个开伞过程中伞衣外形变化及伞衣内外流场的变化情况。通过计算得到如下结论:
(1)初始充气阶段伞衣外形变化为:伞衣底边张开后,气流进入伞衣,在气流作用下,伞衣折叠不分从下到上依次张开,直至气流冲到伞衣顶部,伞顶孔打开。整个初部分从下到上依次张开,直至气流冲到伞衣顶部,伞顶孔打开。整个初始充气阶段,伞衣展开部分外形基本保持较光滑的直筒形状,而非喇叭形。在主充气阶段:空气首先在伞衣顶部聚集,使伞衣顶部膨胀,然后膨胀部分向伞衣底边扩展,直到伞衣完全张满。
(2)对于顶部有伞顶孔的平面圆形伞,当伞顶孔被气流冲开后,伞衣的结构透气性对流场会产生显著影响。但从内外压力系数的变化来看,透气性对伞衣内滞止压力的影响较小,对伞衣外流场结构的影响较大,从而对伞衣外表面的压力影响较大。
(3)对于此类有伞顶空的平面圆形伞,当伞衣充气张开后,伞衣尾部出现气流分离,由于主流和伞顶孔射流分别在漩涡区的两侧都沿顺流方向对旋涡区内空气形成强剪切,因此在一个漩涡区内形成两个相反旋转方向的漩涡。且随着伞衣直径扩张,分离区扩大,主流对漩涡区的剪切面积增大,因此漩涡区两个漩涡中外侧的一个漩涡增大,内测漩涡被挤压至离伞顶更近的区域。
(4)对降落伞充满时的绕流流场进行定量测量,对比计算结果发现,从流场拓扑结构来看,计算结果和实验结果的拓扑结构相似。再从压力场的比较可看出,计算与试验得到的压力系数误差不大。因此所采用的数学模型是可靠的,能通过其计算来定性分析绕伞衣流动的流场特性。
[1]BARBER J,JOHARI H.Experimental investigation of personnel parachute designs using scale model wind tunnel testing[A].16th AIAA Aerodynamic Decelerator Systems Technology Conference[C].Boston:MA.AIAA 2001-2074,2001.
[2]SHANNON M P,GEORGIA A G.Experimentalanalysis ofthe pressure distribution on a 35-foot personnel parachute[C].A-merican Institute of Aeronautics&Ast-ronautics or Published with Permission of Author(s)and/or Author(s)'Sponsoring Organization[R].AIAA 2001-2008 ,2001:114-121.
[3]DESABRAIS K L,JOHARIH.The flow in the near wake of an inflating parachute canopy[R].AIAA 2001-2009,2001:122-130.
[4]DESABRAIS K J.Velocity field measurement s in the near wake of a parachute canopy[D].Doctor Thesis of Worcester Polytechnic Institute.2002.
[5]STEIN K R,BENNEY R J.Parachute inflation:a problem in aero-elasticity[R].US Army Tech.Report,NATICK/TR-94/015,1995.
[6]STEIN K R,BENNEY R,TEZDUYAR T,et al.3-D computation of parachute fluid-structure interactions:performance and control[R].AIAA 99-1714,1999.
[7]STEIN K R,BENNEY R,KALRO V,TEZDUYAR T E,LEONARD J,ACCORSI M.Parachute fluid-structure interactions:3-D computation[J].Compuer Methods in Applied Mechanics and Engineering,2000,190:373-386.
[8]HAUG E,LASRY D,Kermel P.Dynamic simulation of industrial membranes including their interaction with surrounding media[A].Third International Symposium of the SBF 230 Evolution of Natural Structures[C].University of Stuttgart,1994.
[9]SAHU J,COOPER G,BENNEY R.3-D parachute descent analysis using coupled parachute descent codes[A].13th AIAA Aerodynamic Decelerator Systems Technical Conference[C].AIAA paper 99-1580,1999.
[10]余莉,史献林,明晓.降落伞充气过程数值模拟[J].航空学报,2007,28(1):53-57.
[11]蒋崇文,曹义华,苏文翰.轴对称降落伞小迎角稳定下降时流场特性[J].中国空间科学技术,2007,28(2):59-65.
[12]马衍富.降落伞织物的透气性[J].产业用纺织品,1987,5(1):26-30.

