异形遮拦光学系统衍射限MTF数值计算方法研究

齐怀川 黄巧林 胡永力

(北京空间机电研究所,北京100076)

1 引言

空间相机指标参数系统论证和优化设计前,必须对成像系统各个环节的性能进行预估,因此成像链路各个环节的建模和仿真是不可或缺的[1]。作为成像链路的核心,成像系统的性能指标主要取决于光学子系统的性能,而在光学系统性能指标中调制传递函数(MTF)是需要描述的最主要的参量[2]。理论上,衍射限MTF和出瞳端波像差二者共同决定了光学系统的MTF[3],其中衍射限所致MTF是衡量光学系统传递函数重要参量,体现了光学系统的极限性能,它可由光学系统光瞳函数计算得出。但是,实际空间相机的光学系统光瞳函数十分复杂,很难解析表出,这给系统性能预估增加了很多困难。现今比较成熟的光学设计软件虽然可以比较精确地预估光学系统的性能,但是这些软件一般需要有确定的光学系统设计构型。目前,在光学设计不成熟阶段利用光学设计软件无法针对性的开展性能预估的工作。因此,本文针对这一问题首先给出光学系统传递函数MTF的推导,而后分析给出衍射限传递函数MTF的解析表达式,最终根据其特点通过数值计算的方法给出获得光学系统衍射限传递函数的方法,并计算了一些具备不同遮拦的光学系统衍射限传递函数MTF。通过将计算结果同空间高性能光学小相机的光学系统设计软件的计算值进行比较,指标基本符合,验证了本方法的有效性。这种方法为链路分析当中全链路精确建模和性能预估奠定了基础,为实际遥感器的总体论证提出了一种新的途径。

2 空间相机光学系统的理想光学传递函数

理想光学系统的传递函数也就是无像差的光学系统的衍射限光学传递函数(OTF)。由于光学系统入瞳的物理限制将产生衍射效应这是不可避免的,根据空间相机成像特性,可将空间相机光学系统作如下结论:1)光学系统为非相干成像方式;2)光学系统对无穷远处成像,像面的位置在后焦平面上;3)光学系统所成物点光源入瞳处近似为平面波。由此空间相机光学系统的点扩散函数可以表示为[4]

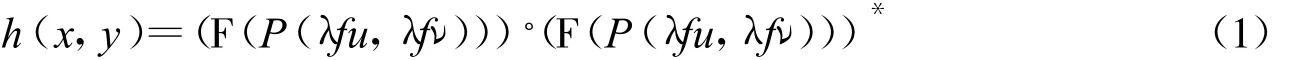
式中 运算符F表示傅里叶变换;*表示求取共轭;λ为光辐射的波长;f为光学系统焦距;u、ν为两个方向的空间频率;P(x,y)代表光瞳函数,即

式中x,y表示光瞳面的空间坐标。

由此可知OTF可以表示为[4]

根据傅里叶变换的性质,式(3)可以表示为

式中 ⊗为相关运算符,由此可以得出光学系统衍射限OTF与光瞳函数P(x,y)的关系。OTF可以表示成相关运算中两错开光瞳函数重叠区域面积与光瞳函数自身围成面积之比,如图1所示。由式(4)可知,当光瞳函数重叠区域面积为零时H(u,ν)为零,即此时为截止频率。当光学系统主镜为直径等于D的圆型孔径,焦距为 f,入射辐射波长为λ时,截止频率满足

图1 光学传递函数求取示意图

式中 fc表示径向截止频率,值得注意的是不考虑波前差的光学系统光瞳函数P(x,y)为实函数,由此可知计算结果就是光学系统衍射限的MTF。

根据上述论述可以推导得出,当光学系统具有中心圆对称圆形遮拦时的衍射限MTF可以表示为[5]

式中D0、Dobs表示主镜尺寸和遮拦尺寸;ur表示径向空间频率;A、B、C都是非常复杂的分量,详见参考文献[5]。虽然该式可以解析表示,但由于形式复杂实际应用并不多,加之实际光学系统遮拦往往不为规则的圆对称形状(比如光轴上的次镜及其支撑连杆构成的遮拦、光学系统主镜中间开口非圆对称等),这就造成了光瞳函数P(x,y)很难用解析式表达。因此,相机初步设计阶段依据式(4)不能预估出光学系统的精确传递函数。为了解决这一问题,本文提出一种数值计算方法来获取异形遮拦光学系统的衍射限MTF。

3 衍射限MTF数值计算方法

将式(4)离散化可得式(6),这样衍射限MTF可以利用计算机通过光瞳函数分布获得赋值的图像矩阵,再求取式(6)自相关和乘积之比后求出衍射限MTF。这样通过离散化,光瞳函数就变成数字图像矩阵;不能解析表达的MTF可以通过编程计算生成数字图像来绘出和求取。

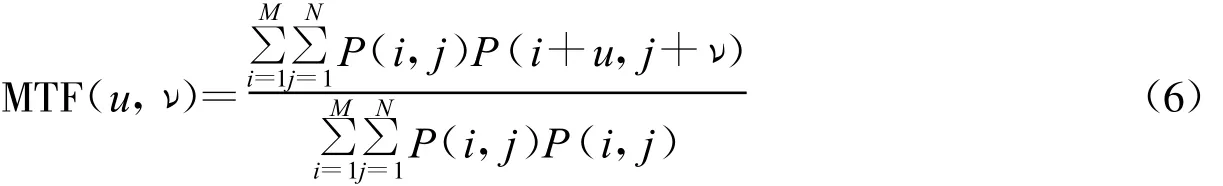
根据具体需求,本文计算程序分成两种类型,其一是根据结构设计要求生成具体光瞳函数的图像矩阵,光瞳函数形状由主镜、次镜及其支撑杆的尺寸、形状及位置确定;第二种是根据光学系统结构设计图进入目标提取子程序的运算获得光瞳函数。具体流程如图2,算法描述如下:

图2 计算MTF程序流程图

(1)光瞳函数生成模式,具体流程如下

1)根据系统遮拦具体要求生成光瞳函数图像。

3)进行如式(6)的离散运算获得MTF(u,ν)矩阵。

4)根据MTF(u,ν)绘出MTF曲线。

(2)光瞳函数提取模式,具体流程如下

1)读入光学系统结构设计图。

2)目标提取,获取光瞳函数有效部分并进行区域分类。

3)生成光瞳函数。

4)获得光瞳函数有效范围大小,根据大小要求以减小边缘效应为准则设置合适图像矩阵大小。

5)进行如式(6)的离散运算获得MTF(u,ν)矩阵。

6)根据MTF(u,ν)绘出MTF曲线。

4 计算实例

运用上述提出的算法进行若干实例计算,检验算法有效性,首先给出光瞳函数生成模式计算实例。根据某相机遮拦比为ε1的光学系统设计,在不考虑支撑杆影响下生成形如图3(a)的光瞳函数图像,图3(b)和图3(c)表示由此求出的系统点扩散函数(PSF)和MTF的图像。同理,考虑次镜支撑杆影响的情况下生成的光瞳函数、PSF、MTF图像如图4(a)(b)(c)。图5为两种情况下MTF(一维曲线)对比情况,横坐标为空间频率对截止频率的归一化f/fc。

图3 某相机遮拦比为ε1的光学系统不考虑支撑杆情况下的计算结果

图4 某相机遮拦比为ε1的光学系统考虑支撑杆情况下的计算结果

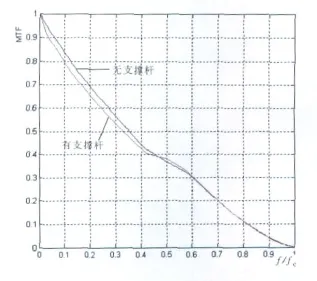
图5 有无支撑杆MTF曲线(一维方向)对比

下面进行复杂遮拦情况下的计算,图6为遮拦比ε2的复杂遮拦光学系统计算得到的光瞳函数、PSF和MTF图像,图7为考虑支撑杆情况下的各个图像。图8为两种情况下MTF(一维)对比情况,横坐标为空间频率对截止频率的归一化f/fc。

图6 遮拦比为ε2的光学系统不考虑支撑杆情况下的计算结果

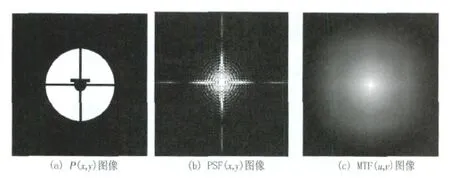
图7 遮拦比为ε2的光学系统考虑支撑杆情况下的计算结果

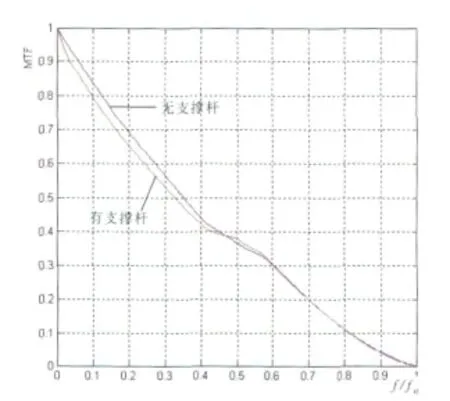
图8 有无支撑杆MTF曲线(一维方向)对比

以下利用CODEV计算高性能光学小相机的设计指标对本方法中获取光瞳函数模式进行验证。应用图像处理方法从相机结构立体图的主镜方向零度视场投影获得其光学系统零度视场光瞳函数P(x,y)见图9,利用文中提出的数值解法获得衍射限PSF(x,y)、MTF(u,ν)如图10。图11为一维方向传递函数函MTF的曲线,横坐标为空间频率对截止频率的归一化 f/fc。表1列出数值解法和CODEV计算的(1/3)fn到2fn处MTF值的差异,由表1可得平均差异小于3%,由此说明二者基本一致。这证明了本方法在光学系统未完成设计阶段,单纯根据光学系统的F数和具体遮拦能够对系统成像性能(衍射限MTF)进行预估以指导遥感器的总体设计。

图9 P(x,y)图像

图10 应用计算程序获得其点扩散函数PSF、传递函数图像MTF

图11 MTF的一维曲线

5 结束语

文中经过理论推导提出了一种获取光学系统衍射限MTF的数值计算方法,以解决不同遮拦光学系统衍射限传递函数MTF的求解问题,其间同空间高性能光学小相机的光学系统设计指标进行比较基本符合,验证了本方法的有效性。本方法的提出使在光学系统详细设计前就能对其极限成像能力进行预估成为可能,为实际遥感器的总体论证提出了一种新的途径,并解决实际工作中的一些问题。异形遮拦光学系统衍射限传递函数的数值求解使光学系统能够精确建模,为结合光学系统波前差求取光学系统精确传递函数和成像全链路的仿真研究提供了必要的条件。

[1]谭维炽,胡金刚.航天器系统工程[M].北京:中国科学技术出版社,2009.

[2]Fiete R D.Image Chain Analysis for Space Imaging Systems[J].Journal of Imaging Science and Technology,2007,51(2):103-109.

[3][美]利齐坎纳尔(Leachtenauer,J C),德里格斯(Driggers R G).监视与侦查成像系统[M].陈世平,马文坡,周峰,等译.北京:中国科学技术出版社,2007.

[4]梁铨廷.波动光学[M].北京:机械工业出版社,1986.

[5]Cota S A,Bell J T.PICASSO-An End-to-End Image Simulation Tool for Space andAirborne Imaging Systems[J].Proc of SPIE,2008,7087-03:1-30.