适用于风电场的最佳电池容量选取的方法

杨水丽，惠 东，李建林，梁 亮，李 蓓

（中国电力科学研究院，北京市，100192）

0 引言

风力发电技术日趋成熟，风电场的建设也在逐步加快。但是，由于风电输出受天气和地理条件等影响具有很大的波动特性，导致风电输出对电力系统的安全性与稳定性会造成很大的影响，这在一定程度上制约了风电的快速发展。因此，为了促进风能的利用与发展，必须减小风电的输出波动。

本文致力于风电输出波动的平滑技术研究，依据成本/性能比，利用计算机仿真来推导获取最佳电池功率与容量。

目前，日本和芬兰等国家对风电功率波动的平滑化进行了比较深入的研究，并提出了应用储能平滑风电波动的运算法则及评估标准[1-2]。在对风电输出波动平滑效果的判据方面，日本的研究者提出了平滑时间常数-电池容量特性和平滑时间常数-系统输出效率特性[2]，依据成本/性能比得出最佳的电池容量。而平滑时间常数-系统输出效率特性的获取依赖于实际应用的储能系统的效率，在储能系统的电池类型未确定的情况下，则存在获取储能系统效率困难的问题，故此判据存在一定的局限性。

在研究平滑时间常数-电池容量特性的基础上，本文提出了一种新的判据，即平滑时间常数-合成输出标准偏差特性。通过分析这2种特性之间的特点，同时依据成本/性能比来确定合适的时间常数，使其既能满足风电输出平滑化的需求，又能使电池容量比较小，而且在储能系统的储能电池未确定的情况下，也能得出最佳的储能系统参数。

1 平滑化原理及评估指标

利用电池存储系统来平滑风电输出的波动，通过控制电池存储系统使风电功率输出和电池存储系统功率输出的总和严格追随着输出目标值。输出目标值的大小通过1个低通滤波器过滤风电输出功率而得到。电池出力要求值为输出目标值与风电出力的差，如果电池输出是正值，表示电池放电；如果电池输出是负值，则表示电池充电。最后，系统输出（合成输出）是电池输出与风电输出的总和。所需存储系统功率与容量的求取在文献[1]中有详细描述。

对风电输出波动平滑的效果分析采用2个评估指标，即风电输出的标准偏差和波动变化率。

（1）标准偏差。

标准偏差可以衡量一个随机变量偏离它的均值程度。若曲线越平滑，标准偏差越小，表征随机变量偏离均值越小。在这里用标准偏差作为评估长时间段内风电输出波动的评估指标。

（2）输出波动的变化率。

波动的变化率为相邻两输出差的绝对值，这是一个评估短时间段内风电输出波动的评估指标。

2 实例计算

实例计算依据张北某风电场49.5 MW级系统的能源管理系统（energy management system，EMS）中10个月（2008年6月—2009年3月）的功率数据，采集时间间隔为5 min，风电功率所测数据如图1所示。

由图1可知，其风电出力特性为：全网风电低于10%额定功率的概率为38%，出力为20%～30%额定功率的概率为14%，而出力超过50%额定功率的概率为15%。对风电出力特性的研究，有益于最佳电池容量选取的经济性分析。

风电功率波动的变化率如图2所示。由图2可知，风电功率波动变化率分布在20%额定功率值（10 MW）范围内，其最大的波动变化率达到40%额定功率值（20 MW）。由此可见，未加入储能系统的风电功率的波动是大而频繁的，因此需要加入储能系统对其波动进行平滑。

依据此风电系统功率测量数据，以不同时间常数t来计算输出目标值，功率积分区间为1天，得出平滑所需的电池功率与电池容量，然后统计电池功率与电池容量的主要概率分布区域，得出最佳的储能系统的功率与容量大小。计算结果如表1所示，不同平滑时间常数下对应的平滑效果如图3所示。

表1 不同平滑时间常数下所需电池功率与容量Tabb.1 Battery power and capacity needed under different time constants

由表1和图3可知，随着平滑时间常数的增大，平滑效果越好，但所需电池功率和电池容量也随之增大。因此，从性能与成本的角度来考虑，需要选取一个既能达到较好的平滑效果，又能比较经济的平滑时间常数。

3 平滑时间常数-合成输出标准偏差特性

由于所需电池功率与容量的求取是以功率积分区间为1天，统计303天（10个月）的电池功率与容量的主要概率分布区域来得出最佳值。因此，则可选取特征日（2008年6月1日）的输出数据来对平滑时间常数-电池容量特性和平滑时间常数-合成输出标准偏差特性进行分析，得出最佳的平滑时间常数。

平滑时间常数与电池容量成正比关系，如图4所示（2008年6月1日）。而标准偏差与平滑效果呈相对的反比关系，因此，可得出时间常数-合成输出标准偏差的特性关系，如图5所示（2008年6月1日）。

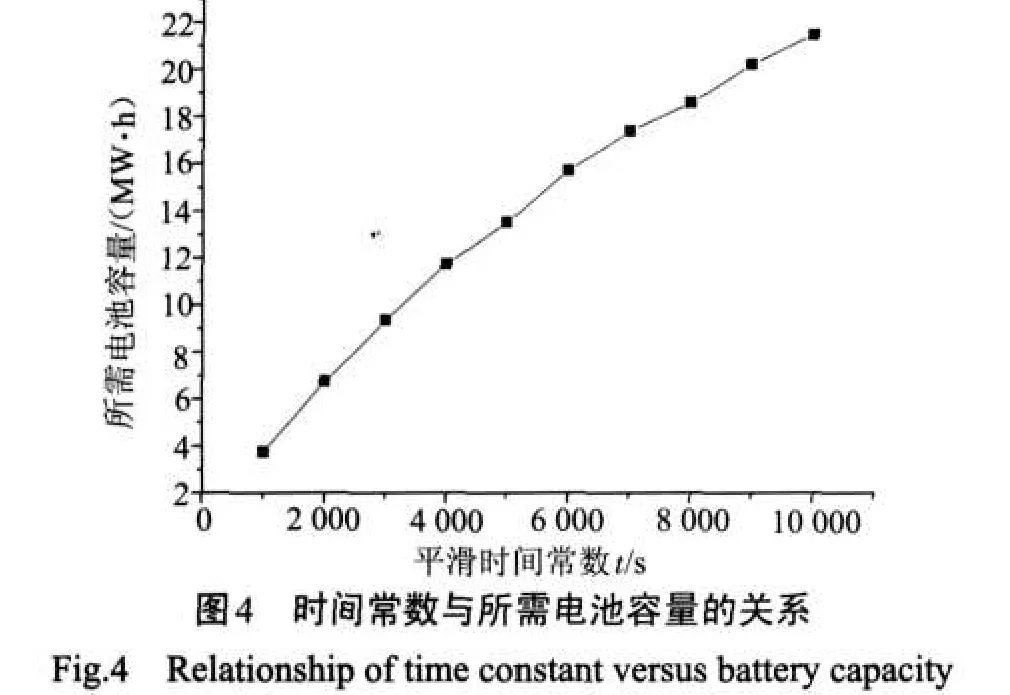
由图5可知，合成输出的标准偏差随时间常数的增加而减小，当时间常数增大，合成输出的标准偏差减小，即表示电池容量越大，合成输出偏离它均值的偏差越小，得到的合成输出曲线越平滑。但当平滑时间常数增大到7000 s的时候，随着平滑时间常数的增大，标准偏差减小的幅度缓慢，对合成输出曲线平滑效果的改善越来越不显著。

由图3也可以非常直观地看出，随着时间常数t的增大，合成出力的曲线愈平滑，但平滑的效果随着t的增大越发地趋于接近，当时间常数超过7000 s后，对平滑效果的改善越来越小。

选择中节能风电场其他日的功率数据进行平滑时间常数-电池容量特性和平滑时间常数-合成输出标准偏差特性分析，仍发现当时间常数超过7000 s后，所需电池容量增大，但对平滑效果的改善越来越不显著。

因此，从成本/性能的视角来说，7000 s是适用于本风电场的最佳平滑时间常数。对应此平滑时间常数的电池功率选取10 MW，电池容量选取50 MW·h，是假定系统设置最佳的参数，如表2所示。

表2 最佳平滑时间常数对应的所需电池功率与容量Tab.2 Battery power and capacity underr optimal time constants

由于风电场风资源的不同，平滑时间常数7000 s不一定是任意50 MW级风电系统的最经济参数，但此判据与推导方法适用于任意功率等级任意风电场储能系统参数的选定。

4 平滑结果分析

选取平滑时间常数7000 s、电池功率10 MW以及电池容量50 MW·h对风电输出进行平滑时，平滑效果通过比较图2和图6（t=7000 s）的功率波动变化率来检验。

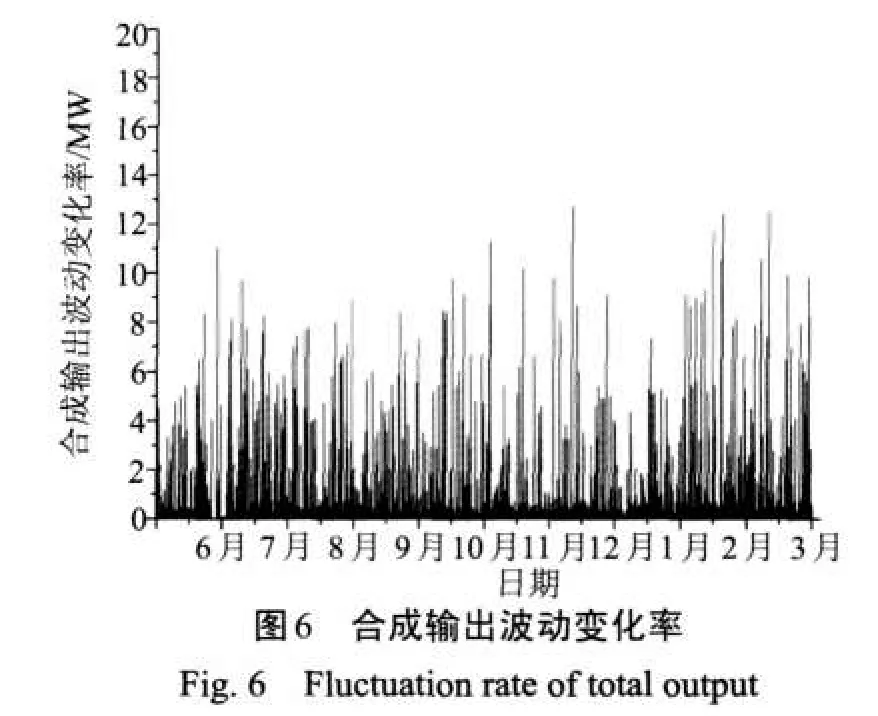
（1）由图2可知，风电原始输出的功率波动变化率主要分布在20%额定功率值（10 MW）范围内，功率波动变化率分布在2%额定功率值（1 MW）范围内的比例为96%；

（2）当选取平滑时间常数t为7000 s进行平滑后，合成输出功率波动的变化率主要集中在4%额定功率值（2 MW）范围内，功率波动变化率分布在2%额定功率值范围内的比例为99.5%，如图6所示。

通过比较得知，对风电出力进行平滑后，功率波动的变化率得到了有效的压制，功率波动的变化率的主要分布区域由20%减小到了4%额定功率值范围内。因此，对功率波动的平滑是成功的。

5 结论

本文通过电池功率、电池容量与平滑效果的定量关系，得出平滑时间常数-电池容量特性与平滑时间常数-合成输出标准偏差特性，依据成本/性能比得到应用于风力发电系统的存储系统最优化的设计。此推导方法适用于不同等级的任意风电场的储能系统参数的选定。

[1]Jukka V P，Peter D L.Effect of energy storage on variations in wind power[J].Wind Energy，2005，8（4）：424-441.

[2]Shiji W，Ryohei O.An investigation on optimal battery capacity in wind power generation system[R].Dept.of EE&Bioscience，Waseda University，Tokyo，Japan.

[3]Key T，GomatomK，Kamath H.Smoothing short-term power fluctuations[R].California,EPRI，2005.

[4]Jantharamin N，Zhang L.A new dynamic model for Lead-Acid batteries[J].Institute of Electrical Engineering CAS，IEEE Xplore，2009：86-90.

[5]Zbigniwe L，Janusz W B.Supervisory control of a wind farm[J].IEEE Transactions on Power Systems，2007，22（3）：985-994.

[6]Mary B，Goran S.Value of bulk energy storage for managing wind power fluctuations[J].IEEE Transactions on Energy Conversion，2007，22（1）：197-205.

[7]Iulian M，Seddik B，Antoneta Iuliana，Energy-Reliability optimization of wind energy conversion systems by sliding mode control[J].IEEE Transactions on Energy Conversion，2008，23（3）：975-985.

[8]Johan H E.Interconnecting large-scale wind power to transmission networks[C].IEEE PES Power Africa 2007 Conference and Exposition Johannesburg，SouthAfrica，2007.

[9]Masashi A，Akihiko Y，Yasuyuki T.Evaluation of battery system for frequency control in interconnected power system with a large penetration of wind power generation[C].International Conference on PowerSystem Technology，North ChinaElectricPower Vniversity，2006：1-7.

[10]Vladislav A，Peter B E.A large wind power system in almost island operation-a Danish case study[J].IEEE，2007，22（3）：937-943.

[11]Chen Z.Issues of connecting wind farms into power systems[C].IEEE/PES Transmission and Distribution Conference&Exhibition∶Asia and Pacific，Dalian，2005.

[12]张步涵，曾 杰，毛承雄，等.电池储能系统在改善并网风电场电能质量和稳定性中的应用[J].电网技术，2006，30（14）：54-58.

[13]李春兰，晁 勤.风电系统电磁暂态数学模型及其仿真[J].计算机仿真，2006，23（4）：220-224.

[14]徐家澎.风力发电场接入系统方案分析[J].内蒙古电力技术，1999，17（6）：6-14.

[15]张红光，张粒子，陈树勇，等.大容量风电场接入电网的暂态稳定特性和调度对策研究[J].中国电机工程学报，2007，27（31）：45-51.

[16]吴义纯，丁 明，张立军.含风电场的电力系统潮流计算[J].中国电机工程学报，2005，25（4）：36-39.

[17]李 蓓，郭剑波，惠 东，等.液流储能电池在电网运行中的效率分析[J].中国电机工程学报，2009，29（35）：1-6.