浅谈圆弧滑动面的验算法

孙哈南

(哈大公路管理处)

1 边坡的剪切破坏

路基边坡滑坍是公路上常见的一种破坏现象,铁路、港口、水坝、河堤等构筑物也时常发生边坡滑坍。因此,对于较高的路堑和路堤(漫水情况下的桥头引道或沙滩路堤)要做稳定性验算。根据土力学原理,路基边城滑坍是由于边坡土体的剪应力超过其抗剪强度而产生剪切破坏。因此,凡是使土体剪应力增加或抗剪强度降低的因素都可以引起边坡滑坍。路基滑动面多为上陡(70°～ 80°)下缓(40°～ 60°)的折线。促使路基变形产生滑坍破坏的因素很多,主要有以下几个方面。

(1)边坡土质。

土的抗剪强度首先取决于土的性质,土质不同则抗剪强度也不同。对路堑边坡来说,除与土或岩石的性质有关以外,还与岩石的风化破碎程度和产状有关。

(2)水的活动。

水是影响边坡稳定的主要因素,边坡的破坏或多或少地与水的活动有关,土体的含水量增加,既降低了土的抗剪强度,又增加了土内的剪应力。在浸水情况下还有水的浮力和水压力作用。

(3)边坡的几何形状。

边坡的高度、坡度等直接关系到土的稳定条件。高大、陡直的边坡,因重心高,稳定条件差,易发生滑坍。

(4)活载增加。

(5)地震及其他振动荷载(爆破等)。

2 圆弧滑动面的验算法

瑞典人 Peeteson在 1916年提出条分法,后经弗兰纽斯(w.Fellinius)补充成为一个完善的方法,并一起沿用至今。

(1)通过坡脚 A任意选定一个可能的圆弧滑动面AD,它的半径为 R。把圆弧以上的滑动土体ABD分成若干个竖向土条,分条宽一般为 2～4m(或 8～10个),假定土条间无侧向作用力,但应结合断面特征分在变坡点或地面坡度变化处以简化计算工作。

(2)计算每一个土条的重量Qi,把它引到圆弧中点上并分解为法向分力和切向分力Ti

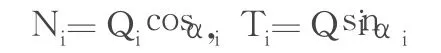
式中;αi为第 i土条圆弧中点法线与铅直线夹角。

(3)以 O点为移动中心,计算圆弧面上各力对 O点的滑动力矩:

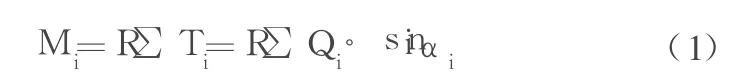
Ti的作用与它所在的位置有关,当它的方向与滑动方向相反时,应取负值,即过 O点作垂线,右侧土条重提供滑动力(+),左侧土条重提供抗滑力(-)。

(4)以 O点为转动中心,计算圆弧面上各力对 O点的抗滑力矩 Mr。它由摩阻力 Nitanφ和内聚力 CL组成,即

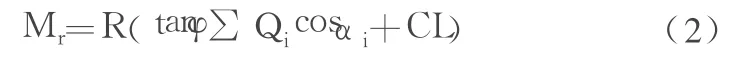
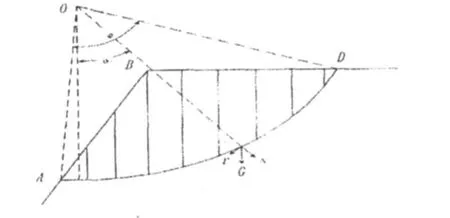
图 1 圆弧法边坡稳定性分析

(5)计算稳定安全系数 k为

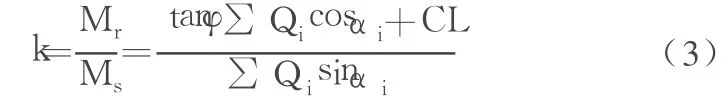
绘若干个滑坍圆弧,依法求出每一个,从中求出kmin,由kmin判断是否稳定(kmin应在 1.25～1.5之间)。

以条分法所得的稳定系数往往偏低,亦即偏于保守。偏低值随滑动圆弧中心角的增大而增大。一般情况下,偏低10%～15%以内,在 φ很大时,可偏低 20%。

(6)圆心的确定。用条分法验算土质边坡稳定性时,圆心位置通常在一条辅助线上,此辅助线的确定有 4.5H法、36°法等。

4.5H法为由坡角 A引垂线,截取高度 H,得 F点;由 F点引水平线,取 4.5H,得 M点;再由 θ(坡角)查 β1、β2后作与 AB成的线,引B水平线,并与之交于 β2角,两者相交得 I点;连接 MI,MI为辅助线。

36°法为过坡顶 B作水平线,作 BF与水平线交于 36°,侧BF为辅助线。

两者相比,36°法简便,但精度不及 4.5H法。一般边坡宜采用 36°法,以求简单。重要边坡宜采用 4.5H法,两者均适用于边坡为(1∶1)～ (1∶1.73)(45°～ 30°)、坡顶水平、滑动圆弧通过坡脚的情况。

辅助线确定后,将各个可能滑弧的两端点连成直线,并在该直线上作中垂线与辅助线相交,所得交点即为各可能滑弧的圆心;或在辅助线上试标出一系列可能的圆弧圆心O1、O2、O3等,由圆心画通过坡脚的圆弧,判断其是否为可能滑动面。如不合适,调整圆心位置,再作弧,直到认为所绘滑动圆弧为最不利时为止。

如果不好判断哪个圆弧为最不利情况,可以由各个不同圆弧及圆心半径求算各个k值,k值最小值对应的圆弧为最不利滑动面。