正弦派生曲线弯道中水沙运动特性动床试验

许 栋，白玉川，谭 艳

正弦派生曲线弯道中水沙运动特性动床试验

许 栋1，白玉川1，谭 艳2

(1. 天津大学建筑工程学院河流海岸工程泥沙研究室，天津 300072；2. 中交第一航务工程勘察设计院有限公司，天津 300222)

为了研究流量和弯曲度对弯道内水流泥沙运动特性的影响，在无黏沙质床面上进行固定边壁动床弯道模型试验，测量不同弯曲度和不同流量组合条件下弯道内的水流运动特性、地形演变和输沙强度．试验表明，水流动力轴线在相邻2个弯顶之间形成过渡段，弯顶下游凸岸一侧存在局部低流速区，该区域最早出现边滩形态；流量与床面形态之间的关系是非线性的，小幅度的流量变化引起较大的床面变化；微弯河道中浅滩、深槽分布规则，当河道弯曲超过一定程度时，显著影响床面的稳定性，床面形态变得复杂；随着弯曲度的增大，河道的输沙能力有减小趋势．

弯道；模型试验；水沙运动；地形演变；输沙强度

弯曲型河流是自然界中最为常见的河流形态之一．与顺直河道相比，弯道水流受离心力影响形成横向水面超高(水面横比降)，同时产生与纵向流动正交的横向水流环流运动(即二次环流)[1]．弯道内的泥沙起动、输移规律和河床的演变规律都受到这种水流结构的深刻影响，例如泥沙的横向输移和分选现象、受弯道曲率影响的边滩与深槽分布以及与弯道曲率无关的交错沙洲的交错分布等[2]．认识天然状态下蜿蜒河流床面形态特征，对于计算河床阻力、判断水流流路以及深泓线变化等具有十分重要的意义[3]．对弯道水动力学和输沙原理的探讨，既是河流动力学中一个富有科学意义的基础理论课题，又因其与弯曲河流河床演变、河道整治工程问题密切相关而一直受到人们的关注．

模型试验是河流动力学研究的重要手段，尤其是对于弯道水沙运动机理这种复杂的水沙耦合作用问题．Whiting等[4]通过在厚10～15,cm的沙质床面上插入阻水薄片形成大幅度(最大偏角大于90°)正弦派生曲线弯道，测量了水流流速、床面地形以及输沙率在弯道内的分布情况，试验流量为1,L/s，弯道波长为2.5,m；Du等[5]利用粒子跟踪测速(particle tracing velocimetry，PTV)系统测量了弯道动床模型中的水流流速分布，研究了弯道表面流场与床面形态之间的关系，试验采用了不同流量(0.3～1.5,L/s)和不同的弯道形态(正弦派生曲线弯道，波长：208～312,cm，最大偏角：12.5°～20°)．此外，Ishigaki等[6]、Patra等[7]、Yilmaz[8]、Kawai等[9]、Yasuharu等[10]、王平义等[11]、魏炳乾等[12]、张土乔等[13]利用室内模型试验针对弯道环流结构、流速重分布特征、水流流态、弯道输沙能力、床面形态和河岸冲刷等进行了研究，丰富了人们对弯道中复杂的水沙运动机理的认识．

Whiting、Du等[4-5]的试验流量和弯道曲率单一或变化范围较小，不利于横向比较．笔者通过在无黏沙质床面上插入透明有机塑料板形成固定边壁动床弯道模型，对不同弯曲度(30°～110°)、不同流量(0.16～ 1.55,L/s)组合条件下弯道内的水流运动特性、弯道地形演变、输沙强度等进行测量，通过不同组次之间的横向比较研究流量和弯曲度对弯道内水流泥沙运动特性的影响．

1 试验装置、试验方法和试验内容

1.1试验装置

试验在一个长4,m、宽1.5,m、深30,cm的室内水池内进行．水池底部由支柱支撑，形成试验平台，水池坡降能够自由调节．水池内铺放厚度10,cm的模型沙，将厚2,mm的透明有机塑料板插入床面泥沙中作为固定河岸，形成固定边壁动床弯道模型．在水池的尾部设水箱储存试验用水，水箱高度低于水池底高程，水箱内设有潜水泵．试验时开启潜水泵，将水流输送到模型河道入口，经消能栅整流后水流进入河道，并在重力作用下沿河道向下游流动，经尾门溢流进入沉沙池，泥沙沉降后水流进入水箱，形成水流的自循环．水泵最大流量为2,L/s，可以通过流量开关进行无级调节．试验装置如图1所示．

图1 试验装置平面布置Fig.1 Layout of experiment device

模型沙选用非均匀河沙，中值粒径为0.73,mm，非均匀系数为1.77，属于中粗沙．值得注意的是，按照动床模型相似理论，模型沙也应遵守几何相似的原理，但是在本试验中如果模型沙粒径按几何比尺缩小，则会使模型沙的物理化学性质发生变化，这使得模型沙的选择变得困难．为了着重体现推移质泥沙的运动，在试验中选择天然沙作为试验用沙，这使得自然塑造成的模型小河与天然河道的河相关系不是正态关系，而是变态关系．

1.2试验方法

试验时在床面上插入透明有机塑料板，形成弯道形态，通水后水流在弯道内流动，并引起河道内床面形态的演变，试验过程中测量弯道内的水流流速和床面地形，研究不同曲率对弯道水动力特性和河床演变规律的影响．主要试验步骤包括：①首先将床面泥沙粗略平整，在水池内加水至淹没泥沙，然后在水下将泥沙铺至水平，放水后调整水池支架的高度，形成均匀坡降；②在床面上根据计算出的坐标点对弯道两岸进行放样，标记出两岸的位置，然后在该位置处插入透明有机塑料板，形成固定河岸；③由于弯道两壁底部未形成密封，水流在试验过程中将从两壁底部向弯道外部的泥沙渗流，引起水流流量的损失，为了减小渗流，试验前向水池内充水，至泥沙中孔隙水饱和；④启动水泵，向弯道中缓慢加水，并逐渐增大至设计流量，流量变化要缓慢，以防止水流冲积引起床面形态的剧烈变化，流量测量采用体积法；⑤当弯道内水位与水池内水位大致相同时，弯道两壁底部渗流基本停止，此时投放示踪粒子，利用PTV系统测量弯道水流表面流场；⑥根据试验需要，每过一段时间进行一次地形测量，测量时首先缓慢减小流量，待水流停止后利用测针对弯道内的地形进行逐个断面测量，根据地形变化的缓急情况选择测量间距，另外，根据地形变化的快慢决定测量时间间隔；⑦试验过程中每5 min从沉沙池内取出沉淀泥沙，测量体积后放入弯道入口处，以维持弯道中泥沙总量的平衡，避免河床的持续下切；⑧一组试验完毕，拆除弯道两壁，重新进行地形平整，重复①～⑦，进行下一组次试验．

试验中水流流速利用PTV系统获得，另外根据粒子运动轨迹分析弯道中的水流动力轴线．床面地形通过测针测量，测点在垂直于河道走向的步长为0.5,cm，沿河道走向的步长根据地形变化的缓急情况，测量间距为5～10,cm．

1.3试验内容

冲积河流的河湾一般可以概化为如图2所示的等宽渠道．图中描述河湾形态的参数包括河湾的直线波长λ、曲线波长M、河道中心线最大偏角ω、波幅A和河宽B．河道中心线可以描述为当地切线偏角φ对曲线长度s的函数，即φ=φ(s )．

试验中采用等宽河道进行试验，河道中心线利用正弦派生曲线进行概化[14]得

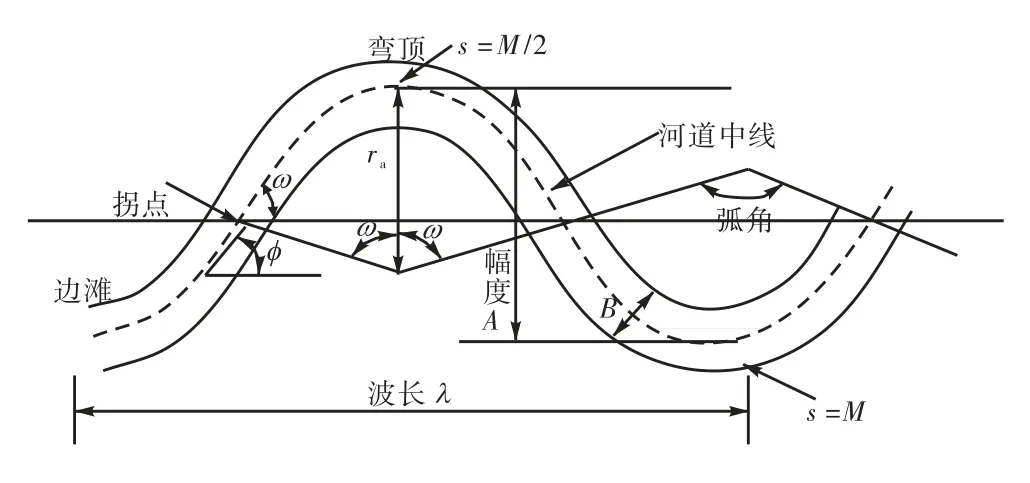
图2 弯曲河道几何形态示意Fig.2 Schematic of the geometric shape of meandering channels

试验过程中将曲线方程转换至平面直角坐标系中，并通过一系列控制点设置初始河道．

采用最大偏角分别为30°、60°和110°的正弦派生曲线弯道，对每种弯道形态利用2～3个不同的流量进行试验，共进行8个组次试验，主要试验参数见表1．

表1 试验组次和主要试验参数Tab.1 Testing runs and main testing parameters

2 试验结果

2.1弯道内的水流运动特性

不同弯曲度的弯道中典型的表面流场测量结果如图3所示．从图3中可以看出，PTV系统的测量结果体现了弯道中表面水流流速分布的基本特征，在弯顶上游附近靠近凸岸处的流速最大，而在水流越过弯顶后，顶冲在弯顶下游的凹岸上，即水流动力轴线由凸岸摆向凹岸，并从此紧贴凹岸向下游流动，直至下一个弯顶．水流动力轴线在相邻2个弯顶之间形成过渡段，凸岸一侧在弯顶下游存在局部低流速区，该区域床面上将最早出现泥沙淤积，形成边滩．试验过程中，示踪粒子投放后大部分将向水流动力轴线处聚集，这一方面是由于弯道环流引起的，弯道环流在床面处由凹岸流向凸岸，而在水面处由凸岸流向凹岸，形成水流垂直于河道方向的横向流速；另一方面，由于动力轴线流速大于其两侧的流速，根据水流运动的伯努利原理，水流对粒子内侧的压力则小于两侧的压力，形成压力差，使得两侧粒子向轴线处聚拢而来．由于弯道中示踪粒子的聚集现象，示踪粒子有时难以布满整个弯道水流表面，粒子缺失处不能有效地测量到流速数据，因此，在PTV系统测量数据后处理过程中，对采集到的原始流速数据进行了插值处理，在一定程度上降低了测量的精度．

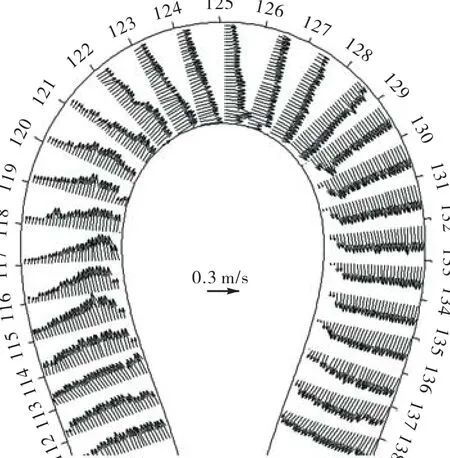
图3 弯道内典型的表面流场结构(单位：cm)Fig.3 Typical velocity distribution in meandering channels(unit：cm)

根据弯道水流流场测量结果，参照视频图像中示踪粒子运动的轨迹，绘制弯道水流动力轴线如图4和图5所示．同一弯道中，当流量不同时，水流动力轴线的位置也不相同，流量较小时，水流动力轴线在弯顶处更加贴近凹岸，且水流在凹岸顶冲点偏向上游；由于不同流量下弯道内水流平均流速变化不大(见表1)，流量的变化反映水深的变化，图4和图5反映的规律为：随着水深的增大，水流动力轴线更加偏向河道中心线．在同一弯道、相同流量的试验过程中，随着弯道内床面的变化，表面流场的分布有较大的调整，在试验经过60,min后，水流动力轴线更加贴近弯道的凹岸，而且在相邻两弯顶之间由一岸调整到另一岸的横向变化梯度更大．这主要是由于在弯道水流结构的作用下，弯道内的床面在凹岸形成深槽而在凸岸形成边滩，从而加剧了水流向凹岸的偏斜．

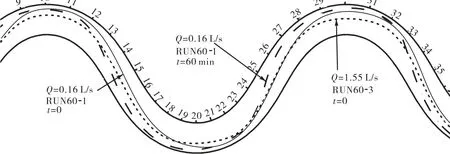
图4 60°弯道中不同时刻和不同流量下的水流动力轴线Fig.4 Dynamic axis of flow in 60°meandering channels at different times with various discharges

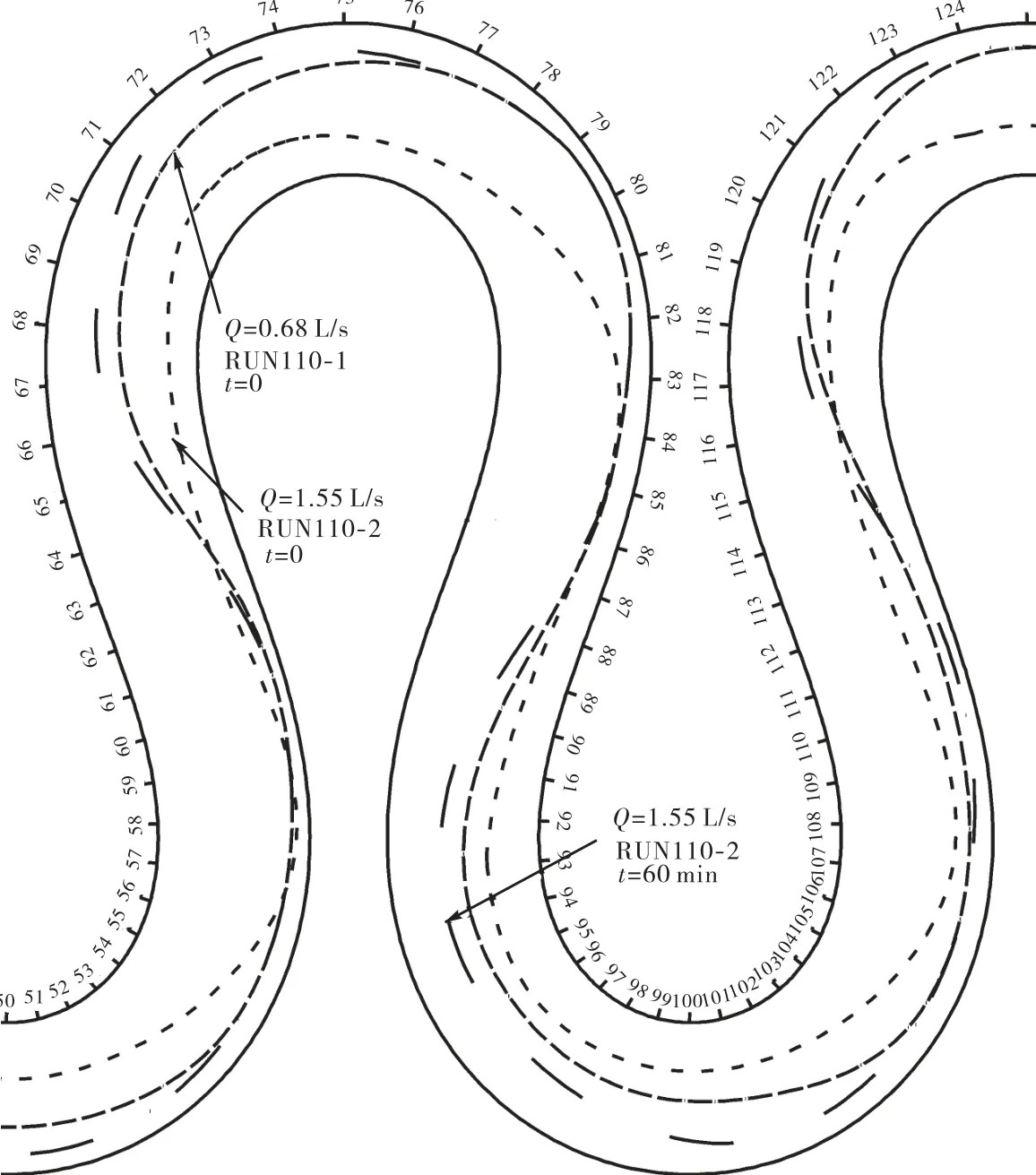
图5 110°弯道中不同时刻和不同流量下的水流动力轴线Fig.5 Dynamic axis of flow in 110°meandering channels at different times with various discharges

2.2弯道内的床面形态演变规律

在河流的动床模型试验中，由于床面具有可冲性，水流的运动将引起床面形态的演变，而床面形态的演变将反过来影响水流的运动，形成水流与床面的耦合作用．当来流量、地形坡降等边界条件长期保持不变时，水流与床面耦合作用的结果就是形成“均衡状态”的河道地形．对于顺直河流，“均衡状态”的河道地形主要有3种沙坡形式：沙纹、沙垄和沙浪，其形态一般较为规则[15]；另外对于宽深比较大的冲积性河流，在河道两岸附近还可能存在交错分布的交错沙洲，使得河流虽然整体保持顺直，但水流流路出现弯曲．无论是沙坡还是交错沙洲，其产生原因都与河床底部水流的不稳定性有关，这些床面形态既存在于顺直河道中，也存在弯曲河道中，其在弯曲河道中的分布与弯道曲率无关[16]．除上述地形外，弯道中还存在与曲率直接相关的床面形态，即边滩，一般出现在凸岸附近．因此实际的弯道中既存在与曲率相关的边滩，又存在与曲率无关的交错沙洲和沙坡形态，这些因素使得弯道内的床面形态变得复杂[16]，在不同的水流条件下，某一种因素可能在床面形态中占主导地位．

最大偏角为30°的弯道内的地形变化如图6所示，图中的参考高程(即零点高程)为整个弯道内床面高度的平均高程．在水流作用1,h左右，弯道内的床面形态基本达到准稳定状态，此时床面起伏变化的幅度达到稳定值约为±2,cm．从图6中可以看出，在弯顶处凸岸稍偏上游处存在边滩；在凹岸处则出现深槽，一般深槽的位置与浅滩相比更偏向上游，与浅滩呈交错分布．浅滩和深槽的这种分布形式与水流动力轴线的位置互相适应．随着时间变化，弯顶处的浅滩和深槽有向下游移动的趋势，如图6(a)和(b)所示；随着流量的增大，深槽的范围有所增大，如图6(a)和(c)所示．

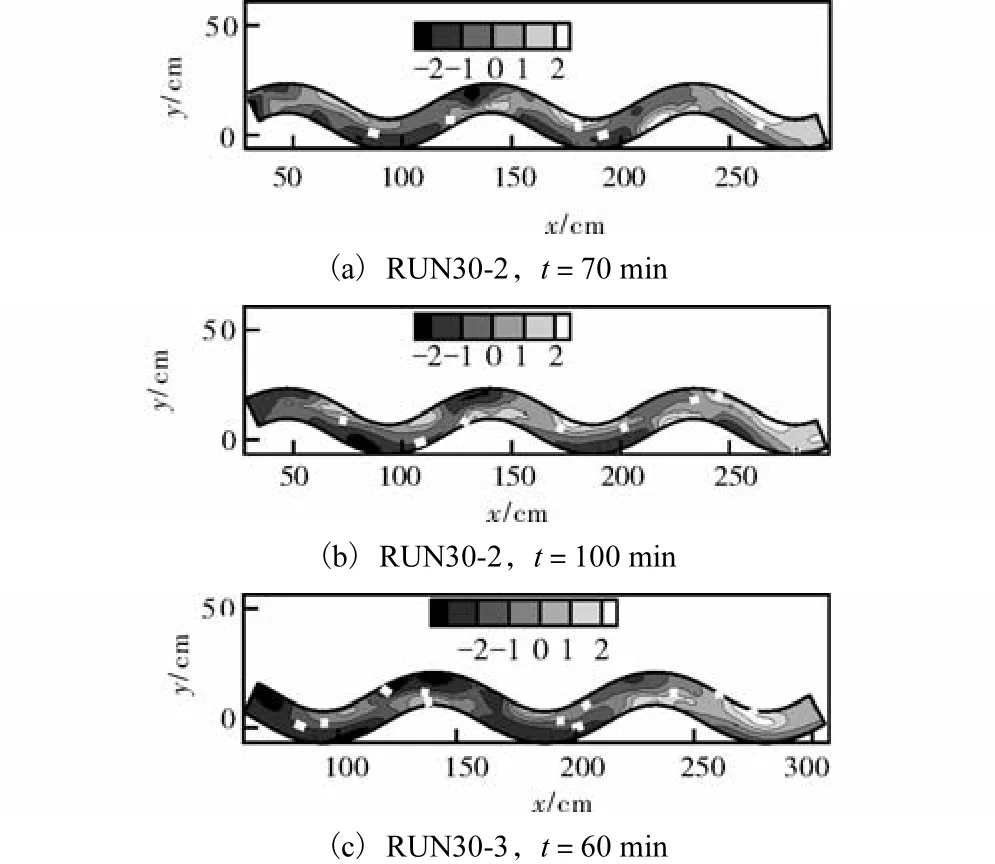
图6 30°弯道内实测床面地形(高程z单位：cm)Fig.6 Topography measured in 30°meandering channels Fig.6 (unit of elevation-z：cm)

为了更清楚地比较不同试验组次中的床面形态，将弯道内左岸(left bank)和右岸(right bank)床面高程z绘制成随河道中心线处距离s变化的曲线，如图7所示．其中床面高程z的参考高程为床面最低高程，这点与床面高程等值线图中的z不同．从图7(a)中左右岸的床面高程曲线上可以清楚看出弯顶处深槽和浅滩的分布，每个浅滩均与一个深槽相对应，且深槽的位置与浅滩相比略向上游偏移．左岸和右岸床面高程曲线在变化趋势上一致，区别仅仅是相差半个周期的相位(见图7(a))．图7(b)中给出了弯道内左岸床面形态随时间的变化趋势，可以看出，在经过30,min水流作用之后，弯道内的床面除了波动幅度有所增大外，有整体向下游迁移的趋势．模型弯道的曲线波长为1,m，在床面形态曲线中波长为1,m的大尺度波动反映的就是弯道中边滩和深槽之间的交替，这种变化与弯道曲率直接相关；而床面形态曲线中波长小于1,m的高频的振荡主要反映2方面的影响因素：交错沙洲和沙坡形态；从图7(b)还可以看出，床面在向下游迁移的同时不规则的交错沙洲和沙纹形态逐渐衰减，水流和床面的相互适应形成了对床面高频振荡的滤波作用．

图7 30°弯道近岸床面高程的沿程变化Fig.7 Streamwise variation of near-bank bed elevation in 30° meandering channels

从图7(c)可以看出，当流量由0.68,L/s增大到1.55,L/s后，约1 h后的床面形态除了波动幅值有所变化外基本相同，流量增大1倍并没有显著改变床面的形态，另外这也说明床面在1,h之内大幅度的变化已经完成．

最大偏角为60°的弯道内的地形变化如图8所示，与最大偏角为30°的弯道地形不同的是浅滩和深槽的位置出现在弯顶下游附近；另外，在弯道凸岸浅滩的形状较为狭长，从一个弯顶下游一直延伸到下一个弯顶附近．弯道内地形的整体沿程坡降较大，上游床面整体高于下游床面．

图8 60° 弯道内实测床面地形(高程z单位：cm)Fig.8 Topography measured in 60°meandering channels (unit of elevation-z：cm)

同一流量下弯道内床面形态随时间的变化如图9(a)所示．在水流的冲刷作用下，床面高程有整体下降的趋势，而波动幅度随时间的变化不大，这说明在大流量(1.55 L/s)情况下，弯道内的地形变化在试验开始阶段较为强烈，而床面在短时间内(＜7,min)就能够接近准稳定状态；随着弯道内浅滩和深槽基本形态的形成，水流和床面逐渐相互适应，床面变化的速度也减慢下来．床面地形减速变化的这种现象在自然界的河流中同样存在，当水流条件突然改变时，如洪水作用，河道内的床面形态会迅速调整，在短时间内变得与水流基本适应；在河湾演变的理论模型中，一般将弯道中的床面视为始终处于准平衡状态[17]，即当水流改变时弯道内的地形立刻调整为与水流相适应的准稳定的状态，其依据就是地形变化所需的时间尺度远小于河岸运动的时间尺度，在河岸微小移动的过程中地形变化即已完成．

流量对地形的影响如图9(b)所示．当流量由0.16,L/s增大至0.68,L/s时，流量变化超过4倍，约1,h后的床面形态变化不大；而当流量由0.68,L/s增大至1.55,L/s时，流量变化仅为2倍，床面形态却发生了较大的变化，这说明流量(或水深)与床面形态之间的关系并非是线性的，在某些情况下，小幅度的流量变化能够引起较大的床面变化，而在其他情况下床面形态对流量变化并不敏感．

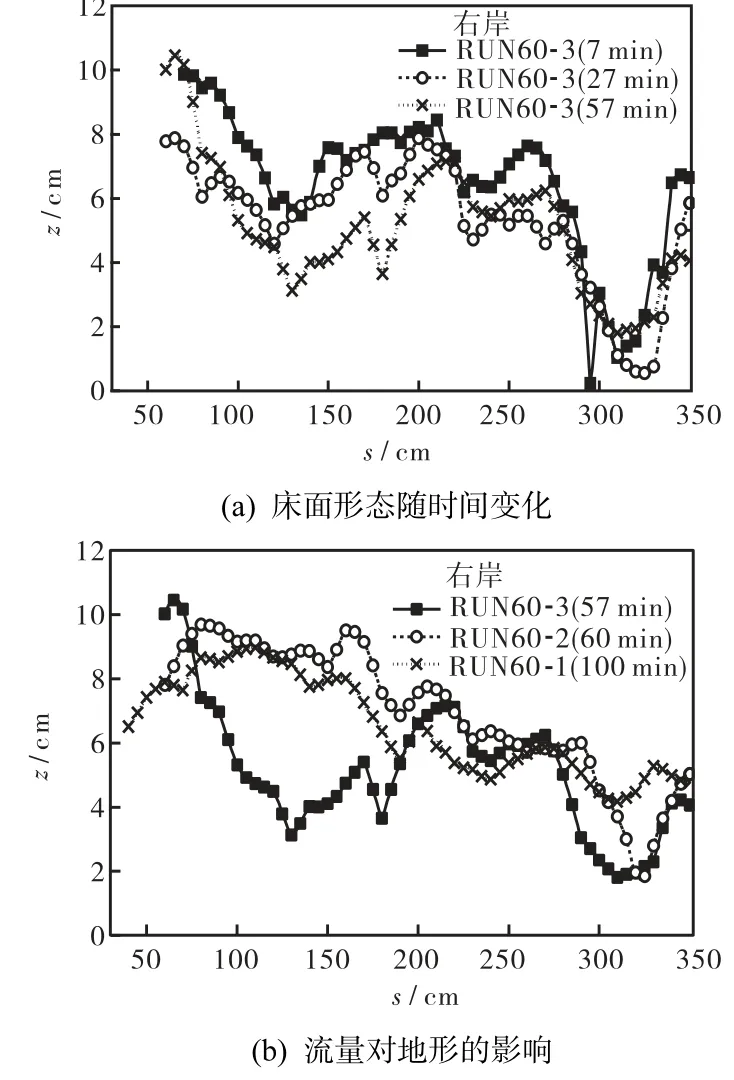
图9 60° 弯道近岸床面高程的沿程变化Fig.9 Streamwise variation of near-bank bed elevation in Fig.9 60°meandering channels

最大偏角为110°的弯道内的地形变化如图10所示．在急弯河道内，地形的沿程变化较为强烈，弯道中除了与曲率直接相关的浅滩和深槽外，还存在沙纹、交错沙洲等成型淤积体，增加了弯道内床面形态的不规则性．另外，地形随时间的变化也较为明显，浅滩和深槽的移动范围较大．当流量为0.68,L/s时，浅滩和深槽在弯道内的位置偏向弯顶的下游，如图10(a)所示；而流量增大至1.55,L/s时，浅滩和深槽的位置略偏向弯顶上游，如图10(b)所示．

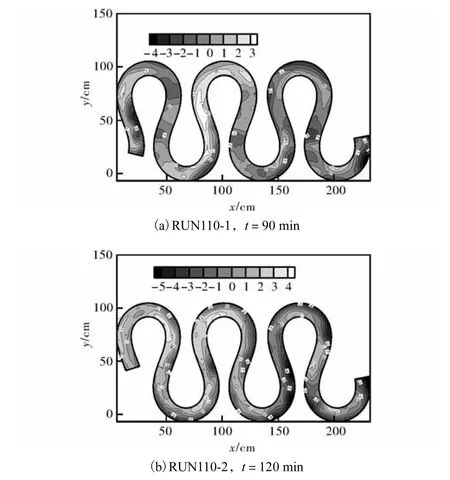
图10 110°弯道内实测床面地形(高程z单位：cm)Fig.10 Topography measured in 110°meandering channels (unit of elevation-z：cm)

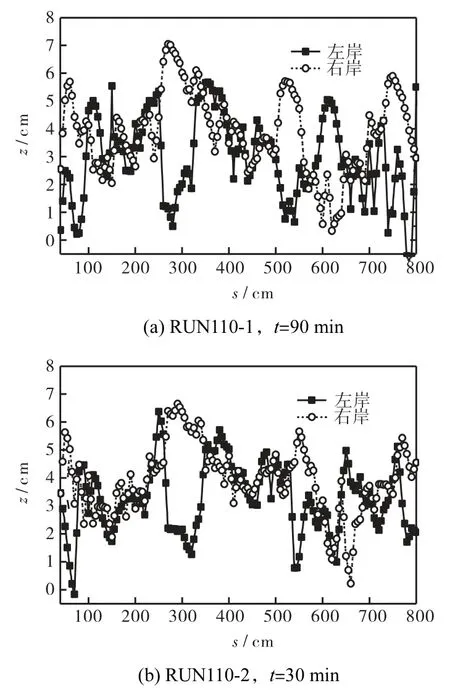
图11 110°弯道左、右岸近岸床面高程的沿程变化Fig.11 Influence of flow rate and time on near-bank bed Fig.11 elevation at both banks in 110°meandering channels

急弯河道内地形的不规则性可以从图11中弯道两岸的地形曲线看出．设计弯道的曲线波长为2.5,m，地形曲线中大尺度的沿程波动与弯道曲率变化相关联，波长为2.5,m，大尺度的边滩分布在弯顶的上游或下游附近．除了随曲率变化的周期性波动外，急弯河道内的地形还存在较显著的小周期波动，体现了边滩与交错沙洲、沙纹形态的共存．对比图11与图7(a)可以看出，110°急弯中的地形起伏比弯曲度较小的30°弯道中复杂得多，这说明并不是曲率越大，弯道内浅滩、深槽的分布就越明显．当河道弯曲超过一定程度时，将会显著影响床面的稳定性，这种不稳定性和弯道曲率共同作用于床面形态，使得急弯河道内的床面形态变得复杂．

110°弯道内流量对床面形态的影响如图12(a)所示．当流量由0.68,L/s增大至1.55,L/s时，弯道内的床面形态变化不大，这点与最大偏角为60°的弯道不同．床面形态随时间的变化如图12(b)所示，从图中可以看出，在30,min之内床面整体形态已经基本稳定，因此在30,～120,min之间床面波动的幅值和波长变化不大，随着床面形态的演变，浅滩和深槽的位置有所改变．

图12 110° 弯道内流量和时间对近岸床面高程的影响Fig.12 Influence of flow rate and time on near-bank bed Fig.1 1 elevation in 110° meandering channels

2.3弯道输沙能力分析

试验过程中，模型河道内的泥沙通过尾门后在沉沙池内沉降，通过测量沉泥沙内收集到的泥沙的体积，获得弯道整体的向下游的输沙能力．试验观察发现，除在深槽边缘受水流紊动的影响有局部泥沙悬扬外，大部分泥沙以推移质的形式向前运动，悬扬后的泥沙在离开深槽后又很快回落到床面，恢复推移质的运动形式．弯道内输沙率随时间的变化如图13所示．整体来看，输沙率随着时间变化有先增大后减小的趋势．在试验开始阶段，水流与床面形态不相适应，弯道内的地形在水流作用下大幅度调整，弯道内具有较大的输沙率，泥沙向尾门输移，但由于尾门稍高于床面，推移质泥沙堆积在尾门附近，此时沉沙池内并未收集到泥沙，输沙率测量值为零；当泥沙堆积达到尾门高度时，泥沙开始越过尾门进入沉沙池．由于床面调整在试验开始阶段较为强烈，开始阶段的输沙率也较大，随着水流和床面的相互协调，输沙率逐渐稳定下来．可以认为，由输沙不平衡所产生的河床变形是朝着使变形停止的方向发展的，这一现象称为河床和水流的自动调整作用[1]．流量对于输沙率有较大的影响，如图13(a)所示，流量的增大不仅增大了平衡状态下弯道的输沙率，也增大了开始阶段输沙率随时间变化的幅度．同一流量(0.68,L/s)下不同弯曲度弯道内的输沙率随时间变化如图13(b)所示，从图中可以看出，随着弯曲度的增大，河道的输沙能力有减小的趋势，这主要是由于河道的弯曲使得水流的流路变长，沿程坡降减小，水流阻力损失增大，从而导致水流输沙效率降低．

图13 弯道内体积输沙率随时间的变化Fig.13 Time history curves of bulk sediment discharge in meandering channels

3 结 论

(1) 在弯顶上游附近靠近凸岸的流速最大，水流动力轴线在相邻两个弯顶之间形成过渡段，弯顶下游凸岸一侧存在局部低流速区，该区域床面上将最早出现边滩形态．试验过程中，示踪粒子在弯道环流的作用下向水流动力轴线处聚集．

(2) 流量与床面形态之间的关系并非是线性的，在某些情况下，小幅度的流量变化能够引起较大的床面变化，而在其他情况下床面形态对流量变化并不敏感．

(3) 试验中30°弯道中浅滩、深槽的分布最为规则，当河道弯曲超过一定程度时，将会显著影响床面的稳定性，使得急弯河道内的床面形态变得复杂．

(4) 随着弯曲度的增大，水流的流路变长，阻力损失增大，使得河道的输沙能力有减小的趋势．

(5) 试验中仅针对微型尺度模型弯道进行水沙运动机理探讨，并不存在实际的原型河流，模型的建立也没有考虑相似准则．此外，模型河道的坡降、水流阻力等一系列复杂条件也与天然河流存在较大差异，这些差异使得试验结果并不能按照某一相似比直接推广到实际河流中．

［1］ 张瑞瑾，谢鉴衡，陈文彪，等. 河流动力学[M]. 武汉：武汉大学出版社，2007．

Zhang Ruijin，Xie Jianheng，Chen Wenbiao，et al. River Dynamics[M]. Wuhan：Wuhan University Press，2007(in Chinese)．

［2］ 魏炳乾，内岛邦秀. 中尺度动床变态模型相似律的研究[J]. 水力发电学报，2004，23(6)：92-97．

Wei Bingqian，Uchijima Kunihide． Study on the similarity laws for meso-scale distorted river model with a movable bed[J]. Journal of Hydroelectric Engineering，2004，23(6)：92-97(in Chinese)．

［3］ 许 栋. 蜿蜒河流演变动力过程的研究[D]. 天津：天津大学建筑工程学院，2008．

Xu Dong. A Study on the Dynamic Process of Meandering Rivers[D]. Tianjin：School of Civil Engineering，Tianjin University，2008(in Chinese)．

［4］ Whiting P J，Dietrich W E. Experimental studies of bed topography and flow patterns in large-amplitude meanders 1：Observations[J]. Water Resources Research，1993，29(11)：3605-3614．

［5］ Du Heqing，Miwa Hajime. Experimental study on the relation of bed morphology with surface flow in meander channels[J]. International Journal of Sediment Research，2006，21(1)：1-12．

［6］ Ishigaki T，Shiono K，Rameshwaran P. PIV and LDA measurements of secondary flow in a meandering channel for overbank flow[J]. Journal of Visualization，2002，5(2)：153-159．

［7］ Patra K C，Kar S K，Bhattacharya A K. Flow and velocity distribution in meandering compound channels[J]. Journal of Hydraulic Engineering，2004，130(5)：398-411．

［8］ Yilmaz Levent. Experimental study of sediment transport in meandering channels[J]. Water Resources Management，2008，22(2)：259-275．

［9］ Kawai S，Julien P Y. Point bar deposits in narrow sharp bends[J]. Journal of Hydraulic Research，1996，34(2)：205-218．

［10］ Watanabe Yasuharu， Sato Koji. Experimental study on bar formations under unsteady flow conditions[C]// Proceedings of the International Conference on Fluvial Hydraulics．The Netherlands，2002：813-823．

［11］ 王平义，文 岑. 冲积河湾蠕动过程的试验研究[J]. 水动力学研究与进展：A辑，2001，16(3)：312-318．

Wang Pingyi，Wen Cen. Experimental study on migration process in alluvial curved rivers[J]. Journal of Hydrodynamics：Ser A，2001，16(3)：312-318(in Chinese)．

［12］ 魏炳乾，孙小军，宁利中，等. 缓变弯道河道冲刷试验研究[J]. 水力发电学报，2007，26(2)：99-103．

Wei Bingqian，Sun Xiaojun，Ning Lizhong，et al. Experimental study on scouring in curved open meandering channel with transition curves[J]. Journal of Hydroelectric Engineering，2007，26(2)：99-103(in Chinese)．

［13］ 张土乔，马 健，孙东坡，等. 复式断面弯道段的水流流态研究[J]. 浙江大学学报：工学版，2007，41(6)：990-994．

Zhang Tuqiao，Ma Jian，Sun Dongpo，et al. Flow pattern of compound section river bend[J]. Journal of Zhejiang University：Engineering Science，2007，41(6)：990-994(in Chinese)．

［14］ Langbein W B，Leopold L B. River Meanders—Theory of Minimum Variance[R]. USA：Geological Survey Professional Paper，1966：H1-H15．

［15］ 钱 宁，万兆惠. 泥沙运动力学[M]. 北京：科学出版社，1983．

Chien Ning，Wan Zhaohui. Mechanics of Sediment Transport[M]. Beijing：Science Press，1983(in Chinese)．

［16］ Johannesson H，Parker G. Linear theory of river meanders[C]// River Meandering Water Resources Monograph 12. Washington，USA，1989：181-214．

［17］ Ikeda Syunsuke，Parker Gary，Sawai Kenji. Bend theory of river meanders (Part 1)：Linear development[J]. Journal of Fluid Mechanics，1981，112：363-377．

Experiment on Characteristics of Flow and Sediment Movement in Sine-Generated Meandering Channels with Movable Bed

XU Dong1，BAI Yu-chuan1，TAN Yan2
(1. Institute for Sediment on River and Coast Engineering，School of Civil Engineering，Tianjin University，Tianjin 300072，China；2. China First Harbour Consultants Company Limited，Tianjin 300222，China)

To investigate the influence of channel sinuousness and flow rate on characteristics of flow and sediment movement in meandering channels，experiments were carried out on the meandering channel model established on a non-coherent sandy bed with fixed sidewalls and movable bed，in which the flow field，topography and sediment transport rate were measured with combination of various sinuousness and flow rates. Test results show that the dynamic axis of flow has a transition section between two adjacent meander crests and there is a local area with low velocity downstream the meander crest near the convex bank，where sand bars first appear on the bed. There isa nonlinear relationship between flow rate and bed topography，and a small change of flow rate may lead to large bed changes. Mildly meandering channels have a regular distribution of point bars and pools and when the channel sinuousness exceeds the critical value，the bed stability will be significantly influenced with complex bed configuration. The sediment transport capability tends to shrink with the increase of channel sinuousness.

meandering channel；model test；flow and sediment movement；topography evolution；sediment transport rate

TV142

A

0493-2137(2010)09-0762-09

2009-05-12；

2009-08-28.

国家重点基础研究发展计划资助项目(2007CB714101)；国家自然科学基金资助项目(50809045).

许 栋（1980— ），男，讲师，博士，xudong@tju.edu.cn.

白玉川，ychbai@tju.edu.cn.