基于CFD的大口径锥管浮子流量计结构设计

朴立华，张 涛，毕丽红

基于CFD的大口径锥管浮子流量计结构设计

朴立华1,2，张 涛1，毕丽红2

(1. 天津大学天津市过程检测与控制重点实验室，天津 300072；2. 石家庄铁路职业技术学院，石家庄 050041)

应用计算流体动力学(CFD)方法，利用“浮子受力平衡度误差分析法”逐步调整入口流速，控制计算精度，对锥管浮子流量计的三维湍流流场进行数值计算，设计出满足设计目标要求的大口径、大流量的金属锥管浮子流量计．为了进一步验证仿真数据的准确性，建立了与实验用流量计结构参数、浮子高度完全相同的6个流量点数值计算模型．物理实验和数值计算数据对比表明，数值计算获得的各流量点的均方根误差仅为1.42%，可以用CFD方法设计浮子流量计的结构参数．

计算流体动力学；大口径；浮子流量计；结构参数；大流量

浮子流量计结构简单、压力损失小、工作特性稳定、应用面广，特别是金属管浮子流量计，工作可靠，是过程控制领域重要的流量仪表之一．目前，为了降低能耗、提高效益，工业界对流量计的精度等级和测量范围的要求越来越高．然而，对于产品的改型，传统上主要是以伯努利方程为依据，依靠生产者的经验以及反复实验进行，成本高、周期长，给新产品开发带来较大困难．计算流体动力学(computational fluid dynamics，CFD)为解决这一问题提供了新途径．与实验方法相比，CFD方法不但能设计出产品的结构参数，而且还可以掌握流场内部压力、速度分布以及流动分离等多方面的数据，具有成本低、周期短、提供信息详实等优势．CFD方法及其应用软件FLUENT早已在飞机、汽轮机等高技术产品的设计中广泛应用．1992年，德国学者Bueckle等[1-2]首次将CFD引入玻璃管浮子流量计研究中，并采用先进的激光多普勒测速技术进行实验测试，结果表明两者具有较好的一致性．

浮子流量计的应用目前还局限于中小管径、中小流量，口径150,mm以上、长度250,mm的短管型金属管浮子流量计尚不多见．笔者利用CFD方法对浮子流量计的三维湍流流场进行数值模拟，设计出了大口径、大流量的金属锥管浮子流量计，并可靠运行于工业现场．

1 浮子流量计工作原理

如图1所示，浮子流量计的检测元件由锥管和沿锥管中心轴上下移动的浮子组成．为了使浮子在锥管中移动时不致碰到管壁，在浮子中心上、下表面分别加装导向杆，保持浮子工作稳定．被测流体自下而上流过浮子流量计时，浮子受到差压力F1、浮力F2和重力W的作用，如图2所示，其中F1和F2构成浮子所受的升力F．若F大于W，浮子便上升．浮子上升时，浮子和锥管间的环形面积随之增大，则环形处流体流速下降，浮子上下截面压差降低，作用于浮子上的升力F随之减少．当F等于W 时，浮子便稳定在某一高度h，由h即可测得体积流量qv，其计算公式为

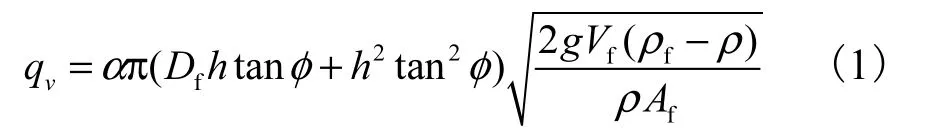
式中：α 为面积系数，无量纲；Df为浮子的最大直径，m；Af为浮子迎流面积，m2；Vf为浮子体积，m3；ρ为流体密度，kg/m3；ρf为浮子密度，kg/m3．

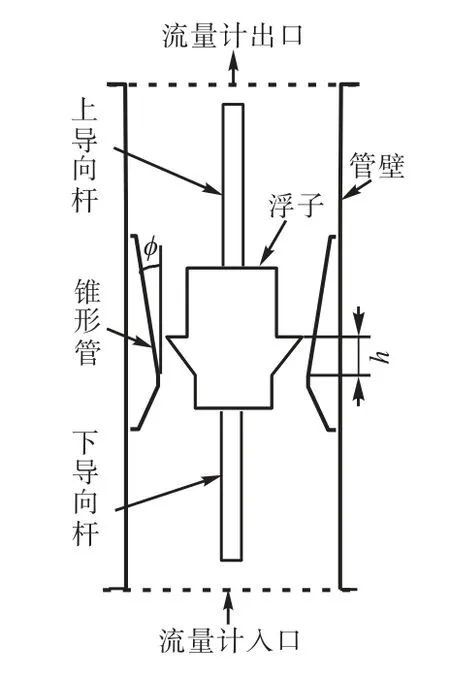
图1 浮子流量计结构示意Fig.1 Schematic diagram of rotameter structure

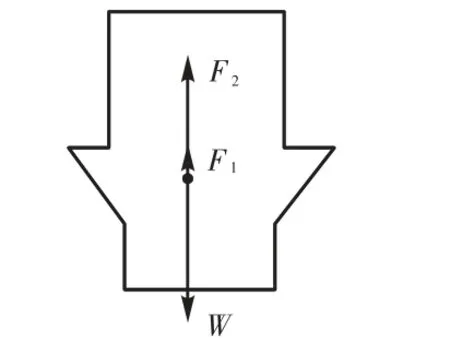
图2 浮子受力Fig.2 Force imposed on float

当锥角φ 很小时，Df≫htanφ，可将h2tan2φ一项忽略不计，这样体积流量qv与浮子高度h之间成为一一对应的近似线性关系[3-4]．早期的金属管浮子流量计各口径长度不一，口径越大，长度也越大．现在，各口径的金属管浮子流量计大都统一制造成250,mm长度的短管型流量计．在进行大流量测量时，由于锥管的长度不变，为达到必要的环通面积，势必要增加φ值，从而导致h2tan2φ一项不能忽略不计，故qv与h之间为非线性关系．一般情况下，线性度随口径的增大而变差．

另一种浮子流量计结构如图3所示，通常称为孔板浮子流量计，在一直管中嵌有一孔板，锥形浮子在其中上下移动，锥管的内锥改为浮子的外锥，便于机械加工．其工作原理与前述锥管浮子流量计类似．

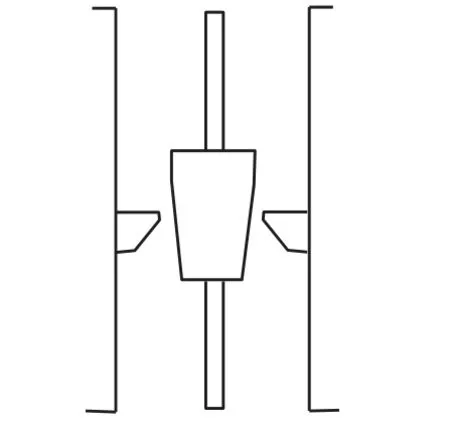
图3 孔板浮子流量计示意Fig.3 Schematic diagram of orifice rotameter

2 结构及参数设计

2.1结构形式选择

浮子流量计的设计目标如下：被测介质为20,℃水，口径200,mm，长度250,mm，流量范围为13.4～134,m3/h，精度等级1.5级，信号输出方式为现场指示和4～20,mA电流输出2种．

根据经验数据，对于大口径浮子流量计，图1所示的锥管浮子流量计的稳定性优于图3所示的孔板浮子流量计，选用锥管浮子流量计；为了保证浮子流量计的稳定性，选用图2所示的圆盘型（记为DFC型)浮子．流量计的结构形式确定为加装DFC型浮子的金属锥管浮子流量计，选用密度为7,900,kg/m3不锈钢材料(1Cr18Ni9Ta)制成．

2.2结构参数设计

流量计的内径D8(见图4)初步定为200,mm，与其口径相同．下面确定图4所示的其他参数．

2.2.1 锥管参数

对于锥管浮子流量计，锥角φ 值是对流量范围影响最大的结构参数，流量上限随φ 值的增大而迅速增大．但是，qv与h之间为非线性关系(见式(1))，增大φ值，必导致qv与h之间的线性度变差．为了平衡上限流量与线性度之间的关系，初步设定φ为6.15°．

显然，若保持D6和H7不变，流量计的上限流量随φ 值的增大(即D7的增大)而增大．H7取常用值65,mm，D7初步设定为186,mm．若在该参数下达不到设计目标要求的上限流量，还可在保持D6不变的情况下增大φ 值，从而使流量计的上限流量加大．锥管的其他参数取值见表1，表中各符号的含义见图4．

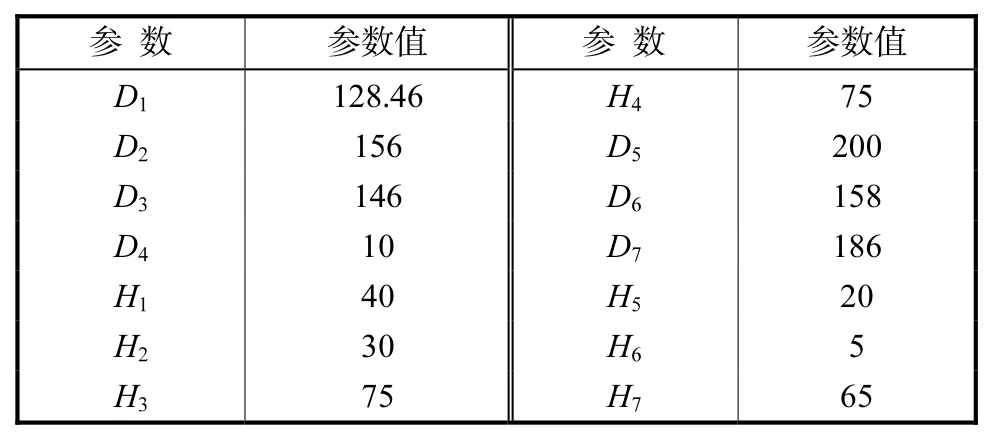
表1 DN200锥管浮子流量计主要结构参数Tab.1 Main structural parameters of DN200 cone rotameter mm

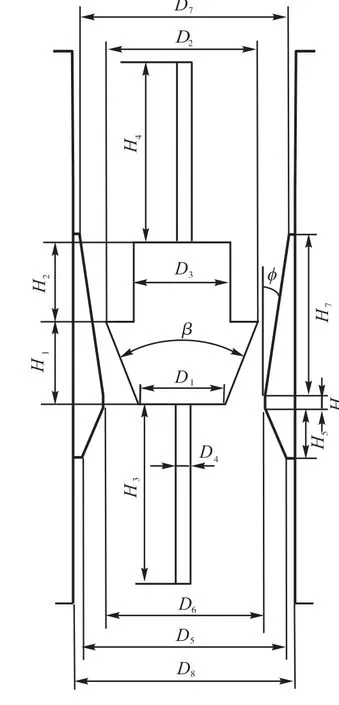
图4 浮子流量计结构参数Fig.4 Structural parameters of rotameter

2.2.2 浮子和导向杆参数

DFC型浮子的角度β在40°～45°之间时，浮子流量计的稳定性较好，初步试算时β值为45°．若在该参数下达不到设计目标要求的上限流量，还可减小β值，从而使流量计的上限流量加大．

流量为0时，浮子最大直径D2位于锥管最小直径D6的上端面．为了保证始动流速在3,m/s以上，D2与D6之间的间隙必须足够小，初步将间隙定为1,mm，故D2确定为156,mm．参数β和D2确定后，浮子形状如图4所示．其余参数见表1．经计算，浮子与导向杆的体积之和为0.001,188,m3，总质量G为92.01,N．

3 CFD仿真计算及参数优化

3.1网格划分

浮子流量计中，支撑架的作用：①为了对浮子上下移动限位；②为了浮子移动时不致碰到管壁．为使数值模型的内部流场尽可能与实际流场一致，建立上、下支撑架模型．在CFD前处理软件GAMBIT中建立的锥管浮子流量计模型见图5．完整的浮子流量计数值计算模型如图6所示，x轴正向为流动方向．为了使流量计入口端面的流动是充分发展的，增加400,mm入口直管段；为了使流动出口是充分发展的，添加600,mm出口直管段．在GAMBIT中，将整个流体域划分为相互连通的入口直管段、浮子流量计和出口直管段3部分．

图5 锥管浮子流量计模型Fig.5 Model of cone rotameter

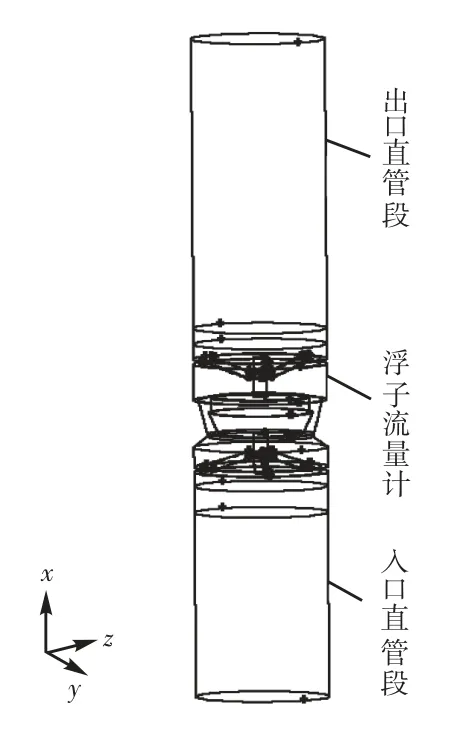
图6 锥管浮子流量计数值计算模型Fig.6 Numerical calculation model for cone rotameter

在GAMBIT中建立计算模型后，导入到CFD应用软件FLUENT中进行流场计算．为了提高计算精度，利用GAMBIT的Size Function功能，从浮子和导向杆的表面开始划分体网格，初始值设为2,mm，最大值设为4,mm，增长率设为1.05[5]．

由于浮子流量计内部结构复杂且不规则，该流体域的网格类型采用四面体网格；为控制网格数量，用六面体网格划分出、入口直管段流体域，网格大小为4,mm．入口边界条件选用速度入口；出口边界条件选用outflow；流量计管体壁面，出、入口直管段壁面，浮子和导向杆的各受力面均为Wall；除浮子、支撑架及导向杆的空间外均连通，且定义为Fluid属性．

3.2计算条件

由浮子流量计的口径、被测介质和流量范围可知，要分析的流场为湍流[6]．利用湍流模型解决工程实际问题，其中最简单实用且计算精度较高，同时也是应用最广的，是标准k-ε模型．选择稳态求解器，湍流中心区利用标准k-ε两方程黏度模型、近壁区采用非平衡的壁面函数法进行计算，根据有限体积法对方程进行差分离散[7]．

流体介质为20,℃的水，密度为998.2,kg/m3，黏度为0.001,003,kg/(m·s)．速度入口边界条件中，湍流参数选择湍流强度和水力直径，湍流强度用默认值，入口为圆管，水力直径即圆管直径200,mm；选用outflow作为出口边界条件；根据实际加工能力设置壁面边界条件Wall中的壁面粗糙度和粗糙常数，粗糙高度设为0.04,mm，粗糙常数设为0.6．求解控制参数中，离散格式选择基于压力-速度耦合的Coupled算法，压力方程使用一阶标准格式，其他方程使用二阶迎风格式．其他参数使用默认值．

3.3初步设计仿真数据

根据上、下导向架的安装位置，浮子最大高度不超过62,mm，分别建立了浮子高度为15,mm,、25,mm、35,mm和62,mm的数值计算模型．

浮子流量计中，浮子和导向杆焊接在一起，故浮子和导向杆所受升力之和等于其重力之和时，浮子才能稳定在某一高度h．FLUENT开始流场计算后，监视残差以及浮子和导向杆所受的升力．当残差收敛到10-4，且升力不再变化时，计算结束．

利用“浮子受力平衡度误差分析法”逐步调整入口流速，控制计算精度[8]．数值计算结果如表2所示．其中，qS为仿真流量，k为利用最小二乘法计算的浮子高度为横坐标、体积流量为纵坐标的线性度值；FS为仿真升力，是浮子和导向杆所受的浮力、差压力和粘性力的合力；当仿真升力与重力G的相对误差不超过0.2%时，得到仿真流量．

从表2中可以看出：浮子高度为62,mm时，仿真流量为111.3,m3/h，低于设计目标130,m3/h的流量要求；如式(1)所示，qv与h之间为非线性关系，但本次仿真数据的k值仅为3.28%，线性度好．

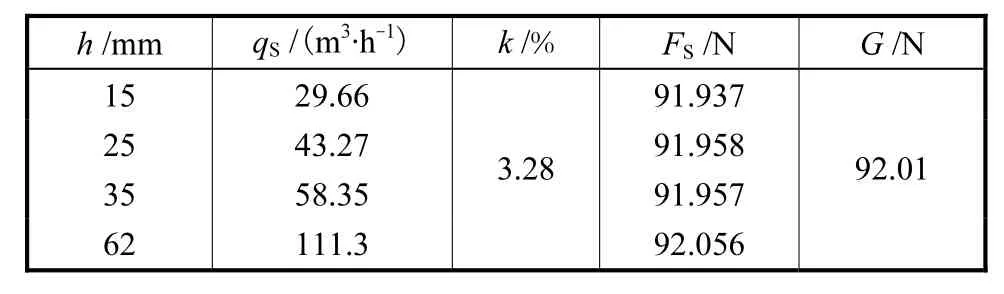
表2 DN200锥管浮子流量计初步设计仿真数据Tab.2 Preliminary design simulation data of DN200 cone rotameter

3.4优化设计仿真数据

根据表2中的数据，需要增大上限流量．如第2.2.1节所述，保持D6不变，增大φ值，上限流量将增大，故将D7增大到198,mm．依据优化后的结构参数，建立浮子高度为62,mm的数值计算模型，数据如表3所示．

表3 DN200锥管浮子流量计优化设计仿真数据Tab.3 Optimal design simulation data of DN200 cone rotameter

从表3可以看出，优化后，浮子高度为62,mm时，仿真流量为153.1,m3/h，高于设计目标要求的流量上限．

4 物理实验

根据数值计算模型的结构参数制造DN200锥管浮子流量计，流量计的参数与前述数值计算模型完全相同．

4.1实验装置

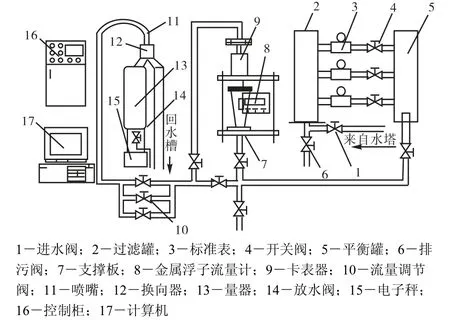
图7 液体流量标准装置Fig.7 Standard facility liquid flow

在图7所示的实验装置上，使用标准表法对浮子流量计进行实验研究．该标准装置采用水塔稳压，流量范围连续可调，能够分别使用称重法和标准表法对流量计进行检定．用称重法对标准表进行检定后，使用标准表法对浮子流量计进行实验，装置准确度为0.15%．

4.2实验数据

在设计流量范围13.4～134,m3/h内，均匀选择包括上限值和下限值在内的11个流量点，分别测量正、反行程下流量计指针在这11个流量点的旋转角度，对正、反行程角度取平均值后，根据平均值做出用流量刻度的表盘；然后，在图7所示的标准装置上检定该流量计，每个流量点正、反行程各检定5次，分别计算各测量值在正、反行程下算术平均值，流量点如表4所示；最后，取下流量计，分别测量表4所示的6个流量点下浮子的高度，并计算各流量点的满度误差δSF，其计算公式为

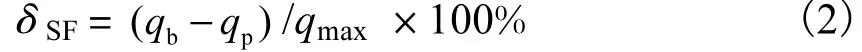
式中：pq为流量计示值流量的平均值，m3/ h；bq为标准表流量，m3/ h；qmax为流量计上限刻度流量，m3/ h．

实验数据如表4所示．从表4可以看出：

(1)满度误差δSF的最大值为0.15%，流量计的精度优于设计目标要求的1.5级；

(2)DN200锥管浮子流量计h-pq线性度为6.53%．

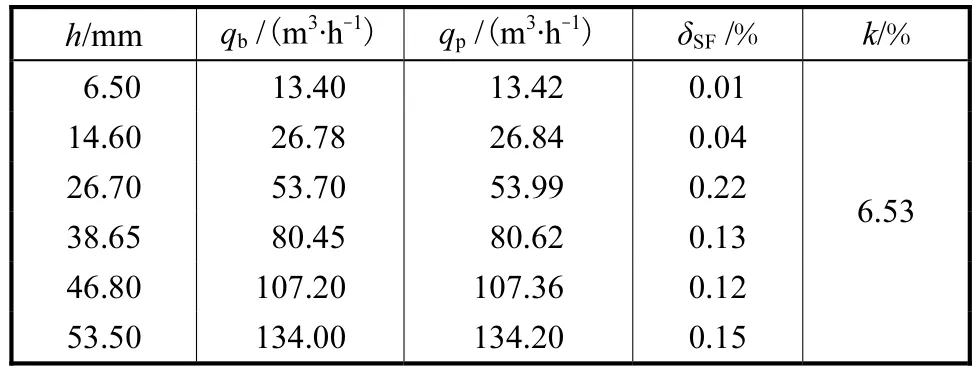
表4 DN200锥管浮子流量计实验数据Tab.4 Experimental data of DN200 cone rotameter

如第2.1节所述，通常250,mm长度的短管型流量计的线性度随口径增大而变差．在相同的实验装置上测试已有的利用实验方法设计的DN100、流量范围6.3～63.0,m3/h和DN50、流量范围1～10,m3/h的锥管浮子流量计，DN100浮子流量计的线性度为12.04%，DN50浮子流量计的线性度为5.39%．对比看出， DN200浮子流量计与DN50浮子流量计接近，优于与DN100浮子流量计的线性度．利用CFD方法确定结构参数并制造的大口径浮子流量计不但满足设计目标要求，而且线性度较好．

4.3非线性修正

金属管浮子流量计指示器的作用是，通过磁耦合将浮子高度h转换并显示为流量qv，构成就地指示型仪表，如式(1)所示，此时h-qv为非线性关系．对于带电信号输出的浮子流量计，目前普遍采用电子的方法将h-qv的非线性关系线性化．

浮子内嵌磁钢，与锥管外一端嵌有小磁钢的机械连杆机构形成内外磁钢磁路耦合．当浮子上下移动时，磁钢同时上下移动，内磁钢的运动引起外磁钢的位移，连杆随之转动一定角度θ，从而将浮子的直线位移转换成角度的位移．在此基础上，采用电容角位移传感器进行机电转换并输出电信号，构成电远传型金属管浮子流量计．利用电容角位移传感器将角度变化转换为电容量值C的变化，再经信号处理电路将电容值的变化转化为电压信号，由微处理器将h-qv的非线性关系线性化后，最终输出4～20,mA线性电流信号[9-12]．

5 实验与仿真数据对比

5.1仿真数据

从表4可以看出，6个实验流量点对应的浮子高度与表2中各数值计算模型的浮子高度并不相同．而且，实验用浮子流量计的D8比数值计算模型的D8大3,mm．为了进一步验证数值计算的准确性，分别建立了与实验用流量计结构参数、浮子高度完全相同的6个流量点的数值计算模型，数据如表5所示．δS为各流量点的均方根误差．其计算公式为

式中：δSF,i为第i个流量点的满度误差；n为流量点个数．

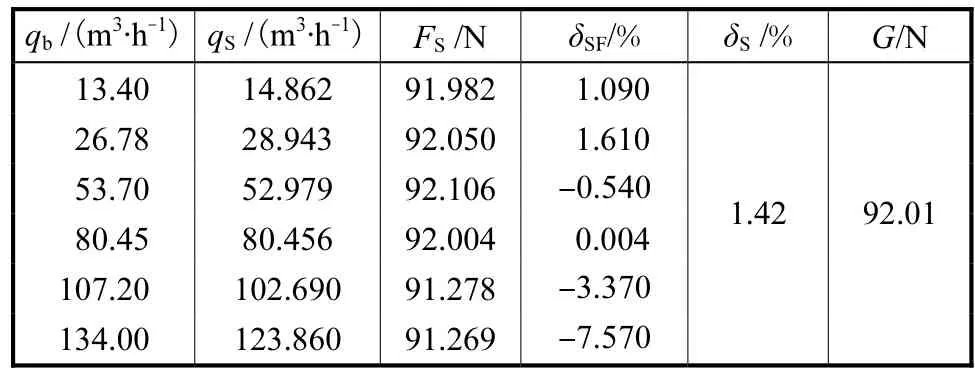
表5 DN200锥管浮子流量计实验与仿真数据对比Tab.5 Comparison between experimental and simulation data of DN200 cone rotameter

从表5可以看出：各流量点的均方根误差为1.42%，误差较小；流量小于满量程的80%时，仿真流量的满度误差较小，而大于满量程的80%时，满度误差变大．

5.2仿真数据分析

表5中的仿真流量与标准表流量相比，误差较小，只有在接近满量程输出时误差较大，主要有以下几方面原因．

(1)建立的数值计算模型的组成和结构参数与浮子流量计相同，并添加了长度合适的出、入口直管段，数值模型的内部流场与实际流场一致．

(2)运用CFD应用软件GAMBIT中的Size Function功能，网格尺寸从浮子和导向杆的表面开始增长，该方法既增加了关键区域的网格密度，降低了网格扭曲率，提高了网格质量，又控制了网格总数，从而降低了仿真误差．

(3)为了进一步降低仿真误差，对FLUENT提供的各种湍流模型进行了详细地比较与分析．在湍流中心区比较并分析了标准k-ε 2方程黏度模型、RNG k-ε模型和Realiable k-ε模型，在近壁区比较并分析了壁面函数法、非平衡的壁面函数法和增强壁面函数法，从而确定了湍流中心区采用标准k-ε 2方程黏度模型、近壁区采用非平衡的壁面函数法的策略．

(4)接近满量程输出时仿真流量qS误差较大，是由浮子流量计的结构决定的．流体在浮子流量计中的流动形态为湍流，浮子流量计内部复杂的几何结构使流体在浮子上、下表面处形成漩涡，流量越大，漩涡越强．利用“浮子受力平衡度误差分析法”判断流场的收敛性时，升力FS是浮子和导向杆表面受力的积分结果，漩涡的存在使积分值不可避免地存在误差，且漩涡越强，误差越大．

多种口径浮子流量计的仿真与实验结果对比表明，当浮子位于锥管顶部附近时，CFD方法计算的仿真流量与实验值的误差在-6%～-8%之间．

6 结 语

利用CFD方法设计出了200,mm口径的短管型金属浮子流量计，满足设计目标对口径、精度和流量范围等技术指标的要求，线性度较好，并可靠运行于工业现场．物理实验和数值计算数据对比表明，数值计算获得的各流量点的均方根误差仅为1.42%，可以用CFD方法设计浮子流量计的结构参数．

［1］ Bueckle U，Durst F，Melling A. Investigation of a floating element flowmeter[J]. Flow Measurement and Instrumentation，1992，3(4)：215-225.

［2］ Bueckle U，Durst F，Melling A. Further investigation of a floating element flowmeter[J]. Flow Measurement and Instrumentation，1995，6(1)：75-78.

［3］ 苏彦勋，梁国伟，盛 健. 流量计量与测试[M]. 北京：中国计量出版社，2007.

Su Yanxun，Liang Guowei，Sheng Jian. Flow Measurement and Testing[M]. Beijing：China Metrology Publishing House，2007(in Chinese).

［4］ JJG257—2007 浮子流量计检定规程[S]. 北京：中国计量出版社，2007.

JJG257—2007 Verification Regulation of Rotameter [S]. Beijing：China Metrology Publishing House，2007(in Chinese).

［5］ Fluent Inc. Gambit Modeling Guide[R]. Fluent Inc，2003.

［6］ 章子雄，董增南. 黏性流体力学[M]. 北京：清华大学出版社，1998.

Zhang Zixiong，Dong Zengnan. Viscous Fluid Dynamics[M]. Beijing：Tsinghua University Press，1998(in Chinese).

［7］ Fluent Inc. Fluent User’s Guide[R].Fluent Inc，2003.

［8］ 徐 英，刘正先，张 涛. 浮子流量计三维湍流流场的数值研究[J]. 天津大学学报，2004，37(1)：74-79.

Xu Ying，Liu Zhengxian，Zhang Tao. Computation of the 3D turbulence flow field of float flowmeter[J]. Journal of Tianjin University，2004，37(1)：74-79(in Chinese).

［9］ 张 涛，徐 英，姜印平，等. 电容角位移式智能金属管浮子流量计的研究[J]. 仪器仪表学报，2003，24(3)：231-235，244.

Zhang Tao，Xu Ying，Jiang Yinping，et al. Investigation of the smart metal tube variable area flowmeter based on the capacitive angular-position transducer[J]. Journal of Scientific Instrument，2003，24(3)：231-235，244(in Chinese).

［10］ 徐淑君，姚 征. 浮子流量计流动特性的非稳态数值研究[J]. 计量学报，2007，28(3)：248-252.

Xu Shujun，Yao Zheng. Unsteady numerical simulation for flow characteristics of float meter [J]. Acta Metrologica Sinica，2007，28(3)：248-252(in Chinese).

［11］ 黄金潮，林清萍. 转子流量计的原理与应用[J]. 中国仪器仪表，2005(4)：54-58.

Huang Jinchao，Lin Qingping. Principle and application of rotameters[J]. China Instrumentation，2005(4)：54-58(in Chinese).

［12］ 孙仁伟. 浮子流量计的发展介绍[J]. 自动化与仪表，2005，20(5)：29-31.

Sun Renwei. The introduction of rotameter development[J]. Automation and Instrumentation，2005，20(5)：29-31(in Chinese).

Structural Design of Large Diameter Cone Rotameter Based on CFD

PIAO Li-hua1,2，ZHANG Tao1，BI Li-hong2
(1. Tianjin Key Laboratory of Process Measurement and Control，Tianjin University，Tianjin 300072，China；2. Shijiazhuang Institute of Railway Technology，Shijiazhuang 050041，China)

Metal cone rotameter with large diameter and large flow range that could meet the objective requirements was designed with computational fluid dynamics (CFD)method and float force balance error analysis method，which controlled the computational precision and conducted numerical calculation of the 3D turbulence flow field of the cone rotameter by adjusting the inlet velocity. In order to further validate the accuracy of simulation data，numerical calculation models for the six traffic points，which had the same stroke and structural parameters as the rotameter in the experiment，were established. Comparison between the results of the physical experiment and numerical computation indicates that the root mean square error of the various traffic points in numerical calculation is only 1.42%. Therefore，CFD method can be used to design the structural parameters of rotameter.

computational fluid dynamics；large diameter；rotameter；structural parameter；large flow

TH814

A

0493-2137(2010)09-0804-06

2009-10-19；

2010-01-12.

朴立华（1975— ），女，讲师，博士研究生，hbpiaolh@163.com.

张 涛，ZT50@tju.edu.cn.