供水管网系统爆管预测

王 祎，田一梅，单金林，张新波，裴 亮

供水管网系统爆管预测

王 祎1，田一梅1，单金林1，张新波2，裴 亮3

(1. 天津大学环境科学与工程学院，天津 300072；2. 天津城市建设学院环境与市政工程系，天津 300384；3.天津天保市政有限公司，天津 300451)

为有效分析管道爆管可能性的大小，并为制定管网更新决策提供依据，以北方某港口城市供水管网实际爆管数据为基础，采用生存分析的方法建立了爆管危险率模型，提出了管道个体的概念，详细分析了选取模型变量的方法，并采用贝叶斯定理将变量分级．结果显示该模型具有较好的拟合效果和预测精度，能够有效地筛选出爆管危险率较大的管道．

供水管网；爆管；预测；生存分析；危险率模型；贝叶斯定理

给水管道爆管事故带来的危害是极其严重的，能够有效预测爆管事故，具有重要意义．爆管预测多囿于数据难收集、影响因素不完备而难以达到较高的精度．国内外的爆管预测研究，大多都具备了足够的数据储备，能够给出精度较高的模型，而基于短期记录数据的研究并不多见．笔者通过分析影响爆管的因素，建立了爆管危险率模型，尝试使用少量数据对爆管可能性进行短期的预测．此外，在爆管研究中应用生存分析时，尝试应用了管道个体的概念．

研究区域内大部分供水管道均在1993年前后建成，管材基本采用灰口铸铁管，脆性较强，抗剪切能力较差，容易发生折断爆管，接口为刚性接口．区域内土壤多为盐碱地，虽然建区时铺设了1.5,m厚的新土，但经过十几年渗透，盐碱度也很大．管道外壁腐蚀老化严重．区域内物流业发达，集装箱车流量很大，但地基条件差，土质松软，管道易发生不均匀沉降、侧移等现象．灰口铸铁管没有防腐内衬，管道内壁易锈蚀，且管道按远期规划设计，直径普遍偏大，导致流速缓慢，结垢现象严重．综上所述，管网已进入老化阶段．

1 爆管预测模型

近年来建立了很多用于分析爆管的统计分析模型[1-7]．本研究中考虑到时间指数模型需要以年爆管次数进行预测，而本研究区域只有2～3年数据，预测效果未必理想，故选择需求数据较少、理论基础扎实的危险率模型．危险率模型是由Cox[8]提出的，随后Andreou等[9-10]深入研究了危险率模型．其形式为

式中：t为时间，a；h(t，Z)为危险函数，表示瞬时爆管危险率(t时刻存活的条件下t+Δt时刻的失效概率)；h0(t)为假定的危险函数基准线；Z为相互作用影响危险函数的协变量向量；b为由回归得出的系数向量．

危险函数的基准线h0(t)可以解释为管道随时间的老化，协变量向量代表能够影响爆管危险的环境和运行的影响因素．

按照Andreou的研究结果，在管道进入老化阶段以后，爆管率会相对保持稳定，与历史爆管次数和管龄几乎无关．使用平均爆管率代替危险函数基准线，则爆管危险函数服从指数分布，其形式为

这种危险率模型，已经发展成生存分析中常用的半参数模型．在生存分析的经典应用中，分析个体一旦失效或死亡，则被淘汰；而供水管网实际运行中，需要考虑管道修复和重复爆管的问题．不能简单地把每个管段作为一个研究个体，可以将管段划分成较短的部分，单独作为个体，使爆管相互独立．当个体长度较小时，个体总数庞大，失效个体对总体数量的影响甚微，可以认为研究总体数量不变．本研究中，依据管道维修中更换管件的长度和作业坑的大小，确定以1 m为个体长度，将供水管道划分为小个体．

2 模型的建立及应用

2.1选取模型变量

选取模型变量，不但要考虑变量对管道老化和爆管的影响程度，还要考虑这一因素对管道爆管危险率是否有筛选的作用．此外，选取模型变量还受到数据来源的限制．

虽然温度、管材、管龄和土壤腐蚀性都从不同角度严重影响了管道的老化，但其在整个区域具有相同或近似相同的作用效果，因而筛选爆管危险率的能力较弱；相反，流速偏低、交通负荷过大这些因素在整个区域内分布不均匀，甚至有很大差异，故可作为筛选的依据．

2.2模型变量分级

2.2.1 流速的分级

采用管网水力分析结果作为管道流速，考虑到流速为0.01,m/s与0.02,m/s都是极小的流速，对管道结垢腐蚀的效果相近．需要确定一个界限，使得水力分析结果在此限度以下时，认为流速缓慢对爆管有重要影响．

采用贝叶斯定理进行分析．以影响管道老化或爆管的特定因素为B，以发生爆管为A1，未发生爆管为A2，计算2006年、2007年数据在不同界限流速下的爆管概率P(AiB)(i=1,2)和因素B出现时爆管概率增大幅度

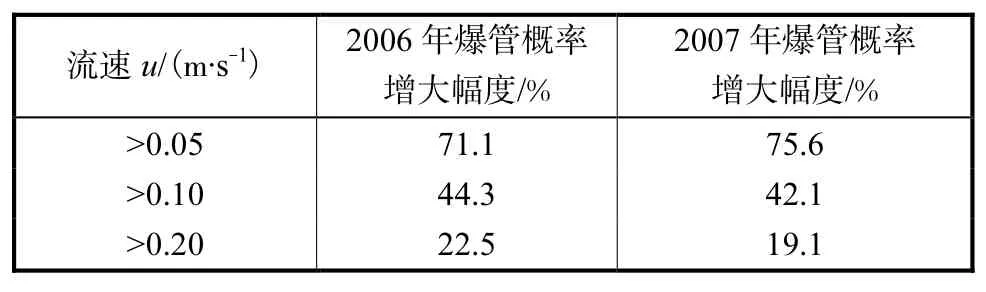
表1 不同界限流速下的爆管概率增大幅度Tab.1 Increase of breakage rate between different water flow velocities

表1中数据表明，当流速低于一定界限时，爆管率显著增大．因而以流速低于0.10 m/s为界限，将全管网分为两级．定义哑变量为

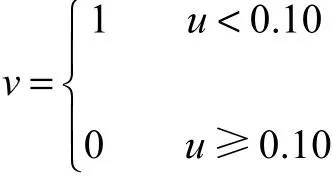
2.2.2 交通负荷的分级

以卫星图片为基础，采用集装箱车流量反映交通负荷，仿照流速分级的方法，对车流量也进行分级．计算2006年、2007年数据在不同集装箱数量界限下的爆管概率增大幅度，列于表2．

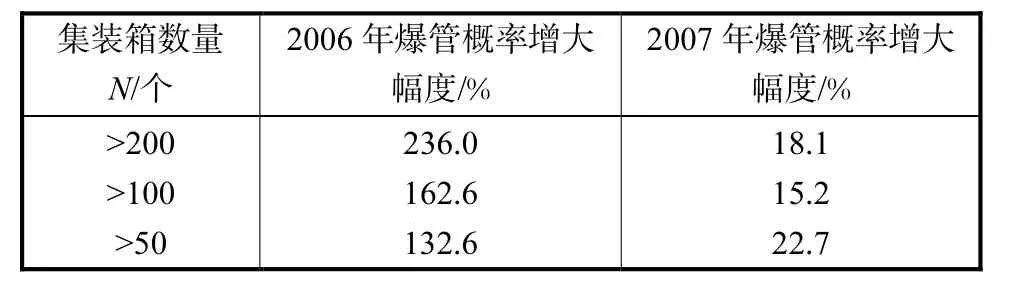
表2 不同集装箱数量界限下的爆管概率增大幅度Tab.2 Increase of breakage rate between different numbers of container

2007年爆管概率增大幅度偏小的原因可能涉及卫星图片的时效性、2006年管网维护、甚至出口政策对仓储物流业的影响等方面．

结合表2数据和以上分析，确定N＞50为集装箱数量的界限，设置哑变量n，取值为

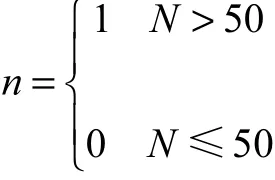
2.3模型求解

考虑到同一时间范围内有可能有多个个体发生爆管，采用有结时的似然估计方法求解模型[11]．在有时间结时的情况下，令di为ti时刻失效的个体总数，Di为ti时刻失效个体的集合，si表示ti时刻所有失效的个体协变量Zj的和，．考虑到样本总体不随时间变化，第m根管段的样本个体数为lm，则任意时刻面临危险的样本总数为1,2,,)D…似然函数为

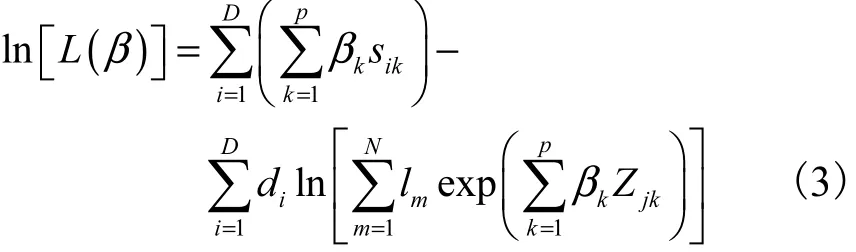
采用Newton-Raphson算法对方程迭代求解．实际应用中发现，以1,m为个体长度，样本数量庞大，发生事故的个体所占比例极小，迭代计算时难以收敛．分析原因可能是过大的样本总数使失效个体的效应变得微乎其微，难以得出规律性的结论，故而将其缩小为1/10，但为体现失效个体的代表性，不删除所有失效的个体．同时为保证所有管道都能够公平地出现在缩小后的总体中，将每根管道的个体数缩减到原来的1/10，为简便计算，直接用管长度的1/10并取整，作为管道的个体数．在这种情况下，迭代计算很快收敛．建立的爆管危险率模型(考虑到管径对管道受力的影响，应予以分别处理[12]．此处以管径200,mm、300,mm为例)为

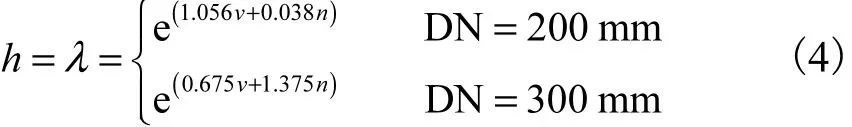
爆管危险率模型计算出的爆管危险率函数只反映一个个体的爆管可能性，而不代表整根管道的爆管可能性．对于一段管长为l，参数为β的管道，其爆管危险率 (以10,m为个体大小)为

这也反映了管长与爆管危险率间的关系，即管道越长，爆管的可能性越大．

2.4模型检验

2.4.1 拟合效果

以DN200爆管危险率模型为例，通过2006年、2007年实际爆管数据分析检验模型的拟合效果．图1显示，2006年共有11根管道发生16次爆管，以爆管危险率h＞80作为高爆管危险率管道的判别标准，全部40根管道中共有13根高危险率管道，其中有8根管道发生爆管事故12次，分别占实际总爆管管道数和总爆管次数的72.7%和75.0%，模型筛选出的高爆管危险率管道中有62.0%发生爆管．

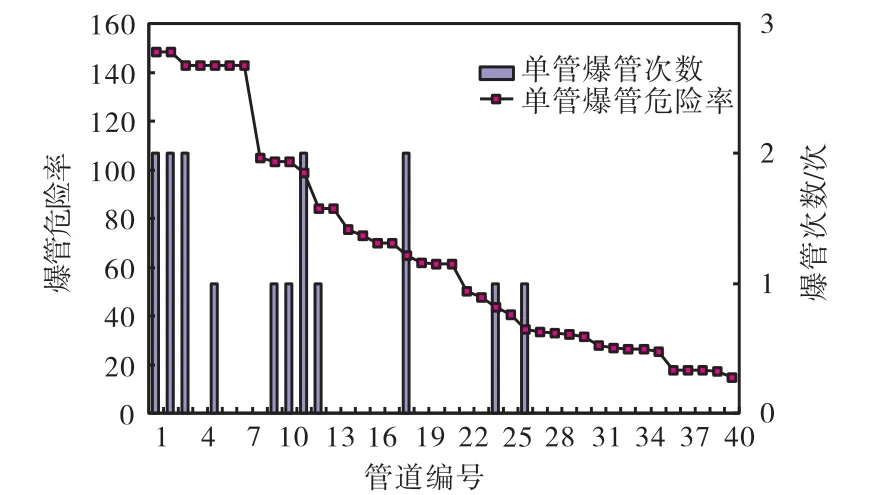
图1 管道爆管危险率与2006年爆管记录分布Fig.1 Pipe breakage hazard rate and pipe failure records in 2006

表3为2006年、2007年的爆管记录(DN200)与爆管危险率模型拟合结果，由此可见该模型具有较好的拟合效果．

表3 爆管危险率模型拟合检验Tab.3 Fitness results of breakage hazard rate model

2.4.2 预测效果

以2008年管网爆管数据为基础，对DN200管道的爆管危险率模型预测精度进行了验证．实际管网在这一时段内有11根管道发生13次爆管．而预测的高爆管危险率的管道中有6根管道发生爆管事故8次，分别占实际总爆管管道数和总爆管次数的54.5%和61.5%，模型筛选出的高爆管危险率管道中有46.2%发生爆管．验证结果表明模型对爆管的预测有较高的精度，可以应用于供水管网的日常管理工作中，从而大幅度提高管网维护的有效性，降低管网爆管率以及爆管造成的社会经济损失．

需要说明的是由于本文中所建立的模型采用的是近2年的爆管影响因素，而且随着影响因素的变化和管道维护的进程，模型只能预测短期内的爆管危险率．若应用于长时段的预测，应及时更新模型参数，使模型始终能够反映管网的现时性．

3 结 论

(1)以供水管网实际爆管数为依据，采用描述型0-1变量对影响因素进行了分级．结果表明，这一方法可以有效筛选出模型变量．

(2)通过对比生存分析的特点和管网的实际情况，提出了研究个体和总体的定义．这种观点解决了将生存分析应用于管道爆管率的预测时如何确定研究个体的问题．

(3)采用常量型危险率模型，以实际数据为基础，建立了研究区域管道爆管危险率模型，经检验，该模型可以有效地筛选出爆管可能性较大的供水管道，可用于依据较少的爆管历史数据制定短期的供水管网更新决策．

(4)相对于回归分析等统计模型，本文应用的方法能够适应数据量小等问题．此外，本文提出的方法是以年爆管可能性为预测对象，因而每年只需计算一次．另外还可以编制计算软件，以提高实用性和易用性．

［1］ Shamir U. An analytic approach to scheduling pipe replacement [J]. Journal of AWWA，1979，71(5)：248-258.

［2］ Walski T M. Economic analysis of water main breaks [J]. Journal of AWWA，1982，74(3)：140-147.

［3］ Yamijala S，Guikema S，Brumbelow K. Statistical models for the analysis of water distribution system pipe break data[J]. Reliability Engineering & System Safety，2009，94(2)：282-293.

［4］ Economou T，Kapelan Z，Bailey T. A zero-inflated Bayesian model for the prediction of water pipe bursts[C]// Water Distribution Systems Analysis 2008. South Africa，2008：724-734．

［5］ Rogers P D， Grigg N S. Failure assessment model to prioritize pipe replacement in water utility asset management[C]// Water Distribution Systems Analysis Symposium 2006. Cincinnati，Ohio，USA，2006：1-17．

［6］ 马乐宁，刘文君，徐洪福. 供水管道爆漏事故影响因素实例分析[J]. 给水排水，2006，32(9)：86-89.

Ma Lening，Liu Wenjun，Xu Hongfu. A case study on factors influencing the burst and leakage of water pipeline[J]. Water & Waste Water Engineering，2006，32(9)：86-89 (in Chinese).

［7］ 于 静，蒋白懿，代 进. 基于极限爆管率的给水管最佳更换时间研究 [J]. 给水排水，2007，33(9)：108-110.

Yu Jing，Jiang Baiyi，Dai Jin. Study on optimal replacement time of water supplying pipelines on basis of threshold break rate [J]. Water & Waste Water Engineering，2007，33(9)：108-110(in Chinese)．

［8］ Cox D R. Regression models and life tables [J]. Journal of Royal Statistic Society，1972，34(B)：187-220.

［9］ Andreou S A，Marks D H，Clark R M. A new methodology for modeling break failure patterns in deteriorating water distribution systems：Theory [J]. Advance in Water Resources，1987，10(1)：2-10.

［10］ Andreou S A，Marks D H，Clark R M. A new methodology for modeling break failure patterns in deteriorating water distribution systems：Applications [J]. Advance in Water Resources，1987，10(1)：11-20.

［11］ 彭 非，王 伟. 生存分析[M]. 北京：中国人民大学出版社，2004.

Peng Fei，Wang Wei. Survival Analysis [M]. Beijing：China People’s University Press，2004(in Chinese)．

［12］ 徐芝纶. 弹性力学 [M]. 北京：高等教育出版社，1990.

Xu Zhilun. Elasticity [M]. Beijing：Higher Education Press，1990(in Chinese)．

Prediction of Pipe Failure in Water Distribution System

WANG Yi1，TIAN Yi-mei1，SHAN Jin-lin1，ZHANG Xin-bo2，PEI Liang3
(1. School of Environmental Science and Engineering，Tianjin University，Tianjin 300072，China；2. Department of Environmental and Municipal Engineering，Tianjin Institute of Urban Construction，Tianjin 300384，China；3. Tianjin Tianbao Municipal Engineering Company Limited，Tianjin 300451，China)

In order to effectively analyze the probability of pipe failure and offer support for decision making in rehabilitation of water distribution system，a breakage hazard rate model was established using survival analysis，on basis of the actual data of pipe failure in the water distribution system in a port city of north China. The concept of individual pipe was introduced，selection method for variables of the model was analyzed in detail，and the variables were classified with Bayesian theorem. Results show that the proposed model has satisfactory fitting performance and prediction accuracy and is able to find the pipes with higher breakage hazard rate.

water distribution system；pipe failure；prediction；survival analysis；hazard rate model；Bayesian theorem

TU991.33

A

0493-2137(2010)09-0840-04

2009-09-14；

2010-01-05.

国家自然科学基金资助项目(50778121)；国家科技支撑计划资助项目(2006BAJ03A10，2006BAJ16B02-01).

王 祎（1983— ），男，博士研究生，vanderebio@gmail.com．

田一梅，ymtian_2000@yahoo.com.cn．