论梁结构损伤的诊断方法

周宁娜,史兴岭,南 洪

(1.陕西通信规划设计研究院,陕西 西安 710065;2.青海黄河上游水电开发有限责任公司建设分公司,青海 西宁 810008;3.中国水电顾问集团 西北勘测设计研究院,陕西 西安 710065)

0 前 言

结构的损伤识别是当前土木工程学科十分活跃的研究领域,该领域的研究有着广泛而深远的工程背景和实际意义。结构在服役期内承载能力的下降被定义为结构损伤,结构构件及其连接部件受损会引起结构损伤,而结构在服役期内的损伤是逐渐形成的。对于土木工程结构来说,结构损伤会引起结构参数(刚度、质量)的变化,结构的模态参数(模态频率、模态振型、模态阻尼)随之发生改变,从而影响到结构的使用性能,一旦损伤积累到一定程度,可能会导致结构整体发生突发性失效,造成巨大的经济损失。因此,适时准确地通过相关参数的检测来确定损伤位置和损伤程度显得尤为重要[1]。钢梁是工程结构的基本单元,广泛应用于水利、土木、建筑等工程结构中,其受载后的裂纹损伤问题是经常导致事故的原因,因而对其进行损伤程度的诊断和预测,以便采取必要的安全措施具有重要意义[2]。本文首先总结回顾了目前结构损伤识别中各种基本方法,并着重介绍了一种改进残余力向量法,并将该方法用于矩形等截面悬臂钢梁的损伤识别,数值模型验证了该方法的有效性。

1 结构损伤识别技术优劣比较

通常工程结构的损伤确定和质量评估分四个层次[3]:①预测结构是否发生损伤;②损伤部位的确定;③损伤严重程度的判别;④结构可维持的寿命等。有关工程结构的损伤识别研究大都局限在①,②两个层次上,而③,④层次的识别还需进一步的探讨,这是由工程结构的复杂性决定的[4]。目前,结构损伤识别领域已发展了许多方法,都有其各自的特点,下面就对这些方法简单的加以评述,指出其优缺点。

1.1 基于振动的损伤识别方法

由于损伤情况的复杂性及位置的隐秘性,很多实验检测装置都难以在施工现场得到实际应用,基于振动的损伤识别技术应运而生,其指导思想为:损伤会引起结构中物理参数(刚度、质量)的改变,结构的模态参数随之发生改变,据此改变量便可确定损伤的位置和程度。其常用的方法如下所述:

基于结构固有频率变化的损伤识别技术:由于固有频率是模态参数中最易测量的参数,并且与测量位置无关,误差小,但频率变化中的低灵敏度要求测量的准确性较高,同时,根据频率变化进行损伤识别有很大的局限性,频率测量不足以对损伤识别提供足够的信息,频率变化只能说明结构中有无损伤,但不能提供损伤的位置及损伤的严重程度。

基于振型变化的损伤识别技术:相对频率而言,模态振型的变化对损伤较为敏感,而且此方法可方便地确定损伤的位置,即损伤的存在可以由频率变化探测到,而确定损伤的位置则需要振型信息。在利用振型变化进行损伤识别中,特征向量测量误差要大于特征值的误差,这些测量误差有时与特征向量扩充导致的误差相混合,导致识别精度不高。于是一系列的改进的振型变化损伤识别技术应运而生,如振型曲率法、振型变化图法和曲率模态振型法等。

基于应变模态的损伤识别技术:结构的振型与频率可以说是结构固有属性的外在表现,而结构的应变模态则可以说是其较为内在的反应,因此,利用结构的应变模态进行损伤识别不能不说是又往深层走了一步[4]。

基于柔度变化的损伤识别技术:其主要原理为柔度矩阵可通过由测试得到的结构前几阶固有频率和模态来较为精确地构造,根据获得损伤前后的两个柔度矩阵的差值矩阵,求出差值矩阵中各列中的最大元素,通过对比每列中的最大元素就可找到损伤的位置[3]。该方法要用到损伤前的结构模态参数,不利于实际应用。于是有学者提出了利用结构损伤模态柔度的曲率进行损伤识别,既有较高的灵敏度,又避免了使用损伤前的结构模态参数。

基于实验模态分析与有限元分析相结合的方法:随着有限元法的发展及计算机的出现,该方法已成为活跃的研究领域。实验模态分析综合了众多的技术,已成为振动工程中的一个重要的组成部分。有限元技术是对真实情况的数值近似,采用合理的假设,建立有限元模型。该方法的一个研究重点即如何使用实验数据来分析有限元模型的误差和改进有限元分析模型;另一个研究的重点为自由度的扩展和缩聚的问题,即实验测得的变形数远小于分析模型的自由度数,必须对实验数据进行扩展或对分析模型结果进行缩减[5]。

基于残余力向量的损伤识别技术:建立残余力向量与损伤结构的刚度和质量矩阵及特征向量之间的关系,从而确定结构的损伤部位,当结构的初始物理参数存在估计误差,或有一定程度的噪声污染时,该法仍能较准确的识别结果。但基于残余力向量的损伤识别技术一般只能诊断出损伤的位置,以及对损伤的程度做出定性判断[6],若要定量地诊断出损伤的程度,还需要结合灵敏度分析[7]。本文在前人工作[7,8]的基础上提出一种改进的基于残余力向量的损伤识别技术,并将其用于矩形等截面悬臂梁的损伤识别,下文将详述这种方法。

1.2 小波分析在损伤识别中的应用[1,5]

由于小波分析非常适合分析非平稳信号,因此可作为损伤识别中信号处理的较理想的工具,用它来构造损伤识别中所需要的特征因子,或直接提取对损伤有用的信息。小波分析在损伤识别中的应用是多方面的,如:奇异信号检测、信噪分离、频带分析等。小波分析是在短时傅立叶谱分析基础上发展起来的,短时傅立叶变换是利用加权函数的形式来表达一个最瞬时的性质。对损伤识别来说,结构局部的损伤往往对应着信号的奇异点,小波分析作为信号处理的有效工具,在时、频两域都具有表征信号局部特征的能力,越来越多地被应用到损伤识别领域。但是小波分析在工程应用中存在一个十分重要的问题就是小波基的选择问题,不同的小波基分析同一个问题会产生不同的结果。因此,小波分析的结果受到所选小波基的限制,通过小波分析得到的小波分量和小波谱只相对所选择的小波基有意义,而不是直接对应于原始数据,这或许是小波应用于损伤识别领域的瓶颈,有待进一步的深入研究。

1.3 基于神经网络的损伤识别方法

近十几年才兴起的神经网络方法除本身具有模式分类功能外,还具有很强的并行推理、适应性学习、联想推理、容错能力,使得它成为一种很好的损伤诊断方法,引起了众多的学者研究运用神经网络方法来进行结构的损伤检测[9]。在实际应用中,通常采用BP神经网络。BP神经网络由于具有较强的非线性映射能力而被广泛用于结构分析中,而且大部分采用三层构造,即一个输入层、一个隐层和一个输出层。其基本思路是:首先用于损伤系统的振动测量数据来训练网络,用适当的学习方法确定网络的参数;然后将系统的输入数据送入网络,网络就有对应的输出,如果学习过程是成功的,当系统特性变化时,系统的输出和网络的输出应该吻合。相反,当系统有损伤时,系统的输出和网络的输出就有一个差异,这个差异就是损伤的一种测度[3]。BP神经网络具有实现简单,算法成熟等优点,但由于具有较大搜索空间,多峰值等问题易陷入局部极值点。故需要和具有全局搜索功能的算法配合使用才能收到较好的效果。如将人工神经网络算法和遗传算法及支持向量机算法联合进行结构损伤识别。

基于振动的损伤识别方法已经在许多领域得到了广泛的应用,并且近些年发展起来的智能损伤识别方法如专家系统、人工神经网络和小波分析等因其强大的信号处理能力而有着不可估量的发展空间和应用前景。

2 改进的残余力向量法理论

对于多自由度的结构体系,忽略阻尼,结构的运动方程为:

式中:M为结构的质量矩阵;K为结构刚度矩阵;¨x为加速度向量;x为位移向量;f为外部作用力向量。

相应的特征方程为:

式中:ω和φ分别为结构的固有频率和特征向量。

令Ku,Mu和Kd,Md分别为结构损伤前后的刚度矩阵和质量矩阵,则对于损伤结构:

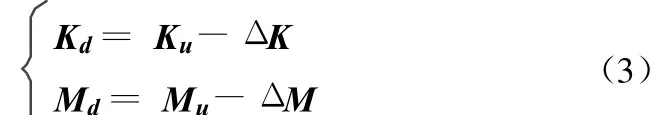
式中:Δ K和Δ M分别为结构损伤引起的刚度矩阵和质量矩阵的变化矩阵,对于损伤结构,它应满足损伤结构自由振动的特征方程:

ωdj和φdj分别为结构损伤后的第j阶固有频率和特征向量。综合式(3)和式(4)可得:

对于式(5)来讲,右边是已知的,记:

定义Rj为损伤结构第j阶模态的残余力向量,则式(5)变为:

对于无损伤结构,Rj=0,而当结构有损伤时,固有频率和特征向量会发生变化,则Rj≠0,式(7)被称为损伤结构的残余力向量方程。在模态分析中认为结构某一单元的损伤只引起单元刚度的下降而不引起单元质量的改变,即ΔM可近似看为零。则式(7)可简化为:

假设梁结构离散为多个单元,结构的整体刚度矩阵K和损伤后的刚度变化矩阵ΔK可以表示为[9]:

其中 P=diag(k1,k2,…,ki,…,kn),Δ P=diag(Δ k1,Δ k2,…,Δ ki,…,Δ kn),ki,Δ ki分别为第 i个单元的轴线刚度(ki=EiAi/li)及其改变量,n为梁结构单元总数,A为结构的刚度联系矩阵,A=[a1,a2,…,ai,…,an],其中 ai为第i个单元的刚度联系向量,结构损伤前后A不变。

将式(9)的第二式展开,可得:

由K的一阶灵敏度分析得[9]:

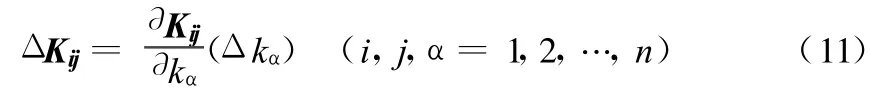
则联合式(10),(11)可得到下式:

由上式可求出刚度联系矩阵A,如上所述,其第i列即为结构第i个单元的刚度联系向量。

Δ K可写为下面的形式:

将上式代入式(8),并令:

则式(8)可化为下面的形式:

其中 η=[η1,η2,…,ηi,…,ηn]。方程(15)可直接求得η,根据式(14)可求得各单元轴向刚度改变量Δki,计算出单元损伤因子αi=Δki/ki,进而可诊断出结构的损伤单元及其损伤程度。

3 数值模拟

考虑一矩形截面悬臂梁800mm×50mm×10mm,弹性模量 E=2.1×1011N/m2,密度ρ=7800 kg/m3。

用弹性模量E的降低来模拟梁结构中的刚度下降,即用弹性模量的折减来模拟损伤,通过有限元分析软件ANSYS模拟悬臂梁刚度下降情况,从梁的固定端开始,用ANSYS将梁离散分为10个单元(采用SHELL63单元),如图1所示:

图1 悬臂梁有限元模型

在建立有限元模型时,假定损伤发生在单元5上,让其弹性模量降低10%。利用ANSYS计算本文所需要的损伤及未损伤结构的模态参数,所建立的有限元模型如图1所示。本文方法仅需使用损伤后结构的第一阶模态参数就可以进行损伤识别[6],由ANSNS计算出所需的第一阶模态参数后,再按照本文的方法进行计算,具体为:由式(12)计算悬臂梁刚度联系矩阵A,A为10×10阶矩阵,由式(6)计算得到第一阶残余力向量,由(15)式求出η,进而根据式(14)可解出Δki,最后计算出单元损伤因子 αi=Δki/ki。图2为悬臂梁损伤诊断结果图。

图2 悬臂梁损伤诊断图

图2中的真实值为本算例人为规定的损伤因子的值,即0.1,诊断值为经过有限元软件ANSYS计算出模态参数并利用本文的方法计算得到的值。由图2可以看出,由本文方法诊断出单元5出现损伤,并且损伤因子的误差约为1.5%,可见该方法具有较高的诊断精度。

4 结 语

本文总结了目前结构损伤识别领域的各种基本方法,对这些方法的优缺点进行了简单的评述,分析了各自的长处与不足。并且在前人研究工作的基础上,提出了用改进的残余力向量法用于梁结构的损伤识别,该方法不仅可以诊断出损伤的位置,还可以定量地诊断出损伤的程度。数值算例也验证了该方法的有效性,可作为梁结构损伤识别的一种有效方法。

[1]丁麟,孟 光,李鸿光.基于Hibert-Huang变换的梁结构损伤识别方法研究[J].振动与冲击,2009,28(9):180-183.

[2]罗跃纲,陈长征,王占国.钢梁损伤的神经网络诊断分析[J].工业建筑,2002,32(1):55-57.

[3]王术新,姜哲.基于结构振动损伤识别技术的研究现状及进展[J].振动与冲击,2004,23(4):99-102.

[4]吴金志,张毅刚.建筑结构损伤识别技术的研究与进展[J].工业建筑,2002,32(增刊):774-781.

[5]李俊萍,李霆.工程结构损伤识别技术的发展现状[J].华北工学院学报,2002,23(5):356-360.

[6]张向东,王志华,马宏伟.基于残余力向量的悬臂梁损伤识别研究[J].太原理工大学学报,2003,34(5):529-531,539.

[7]邹万杰,瞿伟廉,罗 臻.基于改进残余力向量法的桁架结构损伤诊断[J].力学与实践,2009,31(4):40-44.

[8]Doebling S W.Minimum-rank optimal update of elemental stiffness parameters for structural damage dentification[J].AIAA Journal,1996,34(12):2615-2621.

[9]张治国,张谢东.基于遗传算法和神经网络的结构损伤识别研究[J].水利与建筑工程学报,2005,3(3):1-3,7.