被动全向浮标HYFIX定位精度仿真分析

孙 辉，孙明太，刘京莲

(1.海军青岛装备技术质量监测站，山东 青岛 266071;2.海军航空工程学院青岛分院，山东 青岛 266041)

0 引言

被动全向浮标是声纳浮标系列中最简单的一种，具有体积小、重量轻、造价低、方便大量携带等优点，成为反潜平台，特别是反潜巡逻机搜潜作战中使用最多的探测器材。因此对其定位精度的研究有着较大的实际应用价值。

1 HYFIX定位原理

当潜艇急剧转向、变速时，浮标接收到的辐射噪声频率会发生较大偏移，由于潜艇与每个浮标之间的距离不同，各个浮标检测到的偏移会有一个时间差(即时延)(如图1所示)。因此HYFIX(Hyperbolic Fixing)要求2枚以上被动全向浮标同时探测到目标，才能根据时延来确定目标潜艇位置。

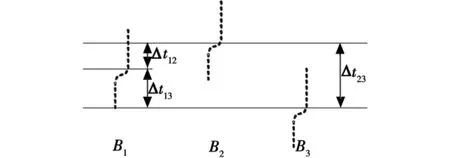
图1 浮标检测目标噪声变化时延示意图Fig.1 Sketch map of time-delay when sonobuoy detecting target noise

由于水下同一深度的海水声速相同，突变的目标潜艇噪声到达两枚浮标的时间差可由式(1)换算成距离差

式中:c为水中声速。

由解析几何可知，到两定点的距离之差为常数的动点的轨迹为一组双曲线，则3枚浮标两两组合可以确定3组双曲线，这3组双曲线的交点(准确地讲应该是一个三角形)即为目标潜艇的位置点。

设在直角坐标系中，被测目标潜艇S(x，y)与各浮标探测点 B1(x1，y1)、B2(x2，y2)、B3(x3，y3)的几何位置如图2所示。

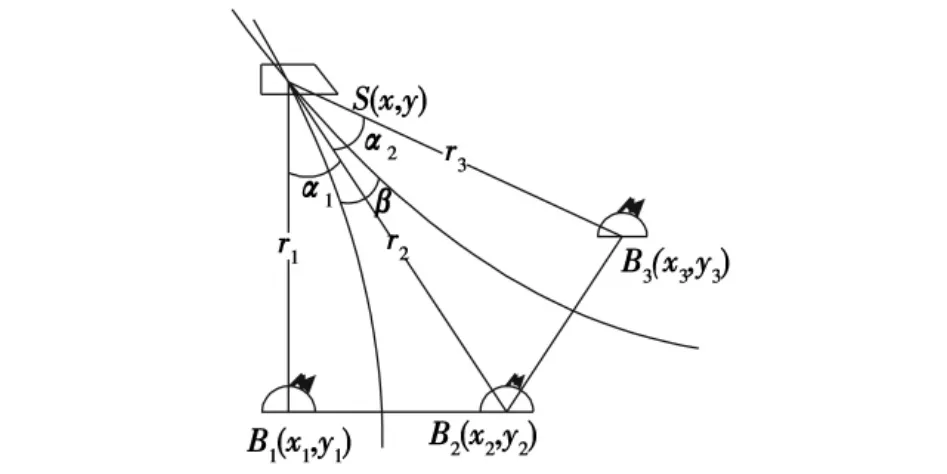
图2 被动全向浮标HYFIX定位原理图Fig.2 Locating principle of HYFIX for passive sonobuoy

根据双曲线定位原理，被探测目标潜艇点声源位置S点的位置坐标理论上可由下列方程组确定为

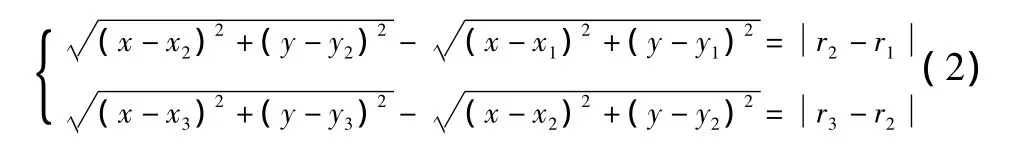
其中:r2－r1=c·Δt1;r3－r2=c·Δt2;ri为各个探测浮标到目标潜艇的距离。

从上式可以看出，目标潜艇的位置点与各个探测浮标的坐标、浮标到目标潜艇之间的距离，以及各枚浮标接收到声信号的时间差有关系。因此，在HYFIX定位精度的分析中，将主要研究浮标位置点误差和系统测时误差对定位精度的影响。

2 HYFIX定位误差模型

在实际定位中，浮标接收声信号受到环境和系统中许多因素的影响，对两枚浮标接收信号时间差的测量可能存在较大的误差。同时，反潜机导航系统精度、海区风速以及流速等的影响，使反潜机测定的浮标坐标、浮标布放间距也存在一定的误差。由文献［4］可知，综合上述误差后的定位误差模型为

式中:β为两条双曲线的夹角(如图2所示);αi为目标潜艇到相邻两枚浮标的夹角;Δti为测时误差。

3 仿真实验

为了较真实地反映各浮标实际位置点和系统测时误差对定位精度的影响，每一次仿真实验都分别计算N=2000次，然后取其平均误差¯δ作为一次定位结果，从而减少偶然性对实验结果的影响。

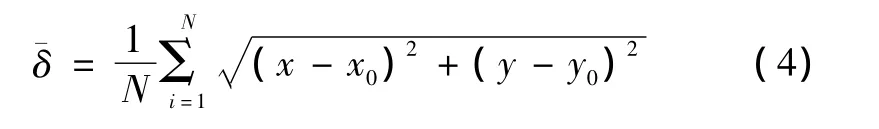
3.1 仿真环境假设

1)在3级海况下，目标潜艇噪声到各枚浮标的声传播速度相同，取c=1500 m/s;

2)反潜机布放浮标时所设定投放间隔时间相同，即相邻两枚浮标理论投放间隔d是相等的;

3)以中间一枚浮标B1为原点，以B1B2的连线为x轴，建立如图3所示的直角坐标系，第3枚浮标B3是取自以B1为圆心，以d为半径的圆上的任意一点;

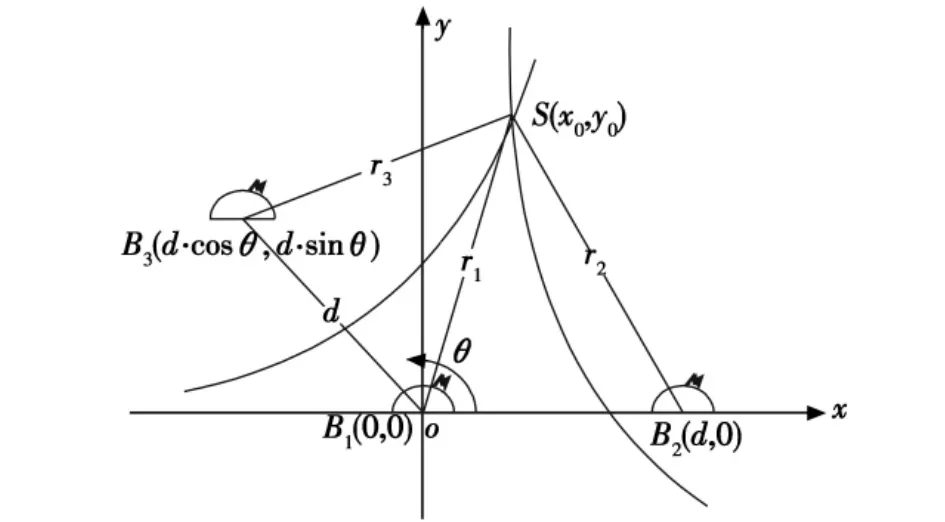
图3 仿真实验所用坐标系Fig.3 Reference frame used in simulation experiment

4)浮标的作用区域是以浮标为圆心，以浮标作用距离为半径的圆;

5)虚解的剔除方法:所求实数交点S(x，y)到任一浮标坐标的距离di小于浮标作用距离ds;

6)在实际定位中，由于飞机导航误差以及风、流等海洋环境的影响，飞机对浮标的定位是存在误差的，主要体现在对浮标间距d的测量上，假设该测距误差服从均值是d，方差是1000的正态分布;

7)鉴于在实际定位中，测时误差大致在0.4～1.0 μs之间，故假设所有测时误差都服从均值为0.64 μs，方差为0.1的正态分布;

8)计算机仿真编程时，时间差Δt1为外层循环变量，时间差Δt2为内层循环变量。

3.2 定位精度分析

在仿真实验中，以中间一枚浮标 B1为原点，以B1、B2的连线为x轴，建立如图3所示的直角坐标系，第3枚浮标B3是取自以B1为圆心，以d为半径的圆上的任意一点，则由式(2)可知:

在文献［6］中提及，在实际定位中，测时误差大致在0.4～1.0 μs之间，故假设此次仿真实验所有的系统测时误差都服从均值为0.64 μs，方差为0.1的正态分布。

1)测量时间差对定位误差的影响。

当浮标作用距离ds=2000 m，浮标布放间距d=ds，3枚浮标夹角θ=30°时，变化浮标接收信号的时间差，得到浮标测量时间差与定位精度的关系图如图4所示。

图4 定位精度与测量时间差的关系图Fig.4 Relation of locating precision and time difference

2)浮标布放阵形对定位误差的影响。

当浮标作用距离ds=2000 m，浮标布放间距d=ds，3枚浮标接收信号的时间差为Δt1=0.5 s，Δt2=0.5 s，变化3枚浮标之间的夹角θ，得到浮标阵形与浮标定位精度的关系图如图5所示。

图5 定位精度与浮标布放阵形的关系图Fig.5 Relation of locating precision and sonobuoy deployment array

3)浮标布放间距对定位误差的影响。

当浮标作用距离ds=2000 m，3枚浮标之间的夹角θ=60°，3枚浮标接收信号的时间差为Δt1=0.7 s，Δt2=0.7 s，变化浮标布放间距d，得到浮标布放间距与定位精度的关系图如图6所示。

图6 定位精度与浮标布放间距的关系图Fig.6 Relation of locating precision and of sonobuoy deployment space

由仿真所得关系图4可以看出:当浮标接收信号时间差趋向于相等时，浮标的定位误差越小。即以原点浮标为基准，目标潜艇到另两枚浮标的距离越趋近于相等，定位误差越小。如图7所示，当潜艇接近于角平分线时，定位误差最小，而在实际应用中也表明:当目标潜艇沿三角阵中线航行通过时，浮标阵对目标潜艇的定位效果最好。

图7 浮标阵形示意图Fig.7 Sketch map of sonobuoy deployment array

由图5中的仿真结果可以看到定位精度与浮标阵型是一个以180°为中心的对称关系。当浮标布放夹角在30°～90°之间时定位误差较小，之后会急剧增大;在接近180°时，如果3枚浮标同时能接收到信号，则潜艇靠近中心浮标，定位误差会有所下降。在实际应用中也表明，如果浮标声纳布放夹角由30°到180°变化，即阵型由三角阵变化为直线阵时，定位精度会减小。从而验证了三角阵的定位精度要优于直线阵的定位精度。

图6所示，当3枚浮标之间距离太近时(1000 m

4 结论

由于在搜潜定位的初始阶段，目标潜艇监听到浮标入水的声响，必然会作出剧烈的变向、变深、变速的反应，这一情况有利于运用HYFIX定位目标潜艇。如果增加保持接触的浮标数量，或者改变浮标布放间隔和阵形(例如采用定位精度相对较高的三角阵)则可以改善这种定位方法。运用连续的定位将给出一组越来越精确的潜艇运动要素估计值，既可以满足攻潜武器的定位精度要求，又可以降低作战成本，提高作战效率。所以，通过以上的仿真分析可以知道，虽然HYFIX定位很难满足攻潜武器的精度要求，绝大多数情况下需使用被动定向浮标或主动浮标进一步精确定位，才能引导攻潜武器对潜艇进行攻击;但被动全向浮标相对于其他种类浮标造价低、经济性好，在搜潜定位的初始阶段使用，可以减少作战费用，因此，在搜潜定位的初始阶段具有较大的应用意义。

［1］孙明太.航空反潜概论［M］.北京:国防工业出版社，1998.

［2］孙明太.航空反潜战术［M］.北京:军事科学出版社，2003.

［3］蔡宗义，赵浚谓，许学忠，等.多基阵无源声测定位算法的研究与仿真［J］.火力与指挥控制，2004，29(4):79-82.

［4］钱世平.侦察原理［M］.西安:第二炮兵学院，1996.

［5］费业泰.数据分析与误差理论［M］.北京:机械工业出版社，1981.

［6］颜喜中.反潜直升机声纳浮标搜潜模型研究与分析［D］.青岛:海军潜艇学院，2003.

［7］赵绪明.航空搜潜战术模型与仿真研究［D］.烟台:海军航空工程学院，2005.

［8］董志荣.被动声纳浮标目标运动分析数学模型［J］.电光与控制，2006，28(6):31-34.

［9］董志荣.水面舰艇立体反潜系统构想［J］.电光与控制，2008，15(5):12-15.

［10］董志荣.舷侧阵声纳浮标目标运动分析数学模型［J］.电光与控制，2007，14(2):16-19.

［11］董志荣.拖曳线列阵目标运动分析数学模型［J］.电光与控制，2007，14(5):34-42.

［12］刘新爱.应用仿真技术的空地导弹命中精度评定［J］.电光与控制，2008，15(3):79-81.