关于配点型无网格法边界条件处理技术

张宏伟, 李美香, 李卫国

(大连理工大学数学科学学院,辽宁大连 116024)

0 引 言

无网格方法是过去十多年兴起的数值方法,该方法是利用一组散布在问题域及其边界上的节点表示该问题域和其边界,通过几个互不相关节点上的值拟合出一个逼近函数,该函数具有较好的光滑性而且导数连续,这样不仅摆脱了网格的束缚,避免了复杂的网格生成及重新划分工作,而且提供了连续性好、形式灵活的形函数.该方法在函数的逼近、边界条件的引入和能量泛函的积分等方面具有一定的灵活性,此外,还具有精度高、前后处理比有限元简便等特性.因此,无网格法可以用来处理大量的基于网格单元的计算方法难以求解的问题,具有有限元法和有限差分法不可比拟的优点.现有的无网格法基本上可以分为Galerkin型(如 EFGM[1]、RKPM[2]等)和配点型(如 SPH[3]、RBF[4]等)两大类.Galerkin法具有良好的稳定性和精确性,通过积分运算降低了对形函数的连续性要求,可方便地施加导数边界条件.但Galerkin法需要布置背景无网格进行数值积分,计算量大.另外,Galerkin法要求形函数具有全局相容性,处理本质边界条件困难.配点型无网格法是真正的无网格法,它应用于实际的关键问题是导数边界条件的存在.边界条件对微分方程至关重要,但导数边界条件才是造成基于任意节点的配点型无网格方法精度偏低且稳定性差的真正原因.本文将介绍配点型无网格法及其特点,对配点法中几种流行的导数边界条件处理技术进行详细的探讨.着重利用有限差分法中的积分插值法,对一维问题的导数边界条件提出操作简单、计算精度高、不增加自由度的较理想的解决方案,并通过具体的数值例子说明它的优越性.

1 配点格式及特点

设在问题域Ψ(其边界为Γ)上未知函数u(x)满足的微分方程为

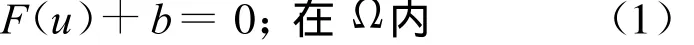
和边界条件

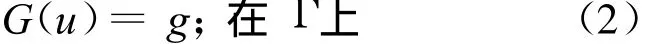
其中F和G是变量的微分算子.

配点法是使微分方程在问题域上的一组特定的点上成立.设函数u(x)的无网格近似函数为uh(x)(各近似函数的构造方法可参看文献[5]),r1和r2分别为计算微分方程和边界条件的配点个数 ,且r=r1+r2,则有配点法的实质是强迫残量在r个配点上等于零.r大于或等于待求参量的个数.配点型无网格法有以下特点:

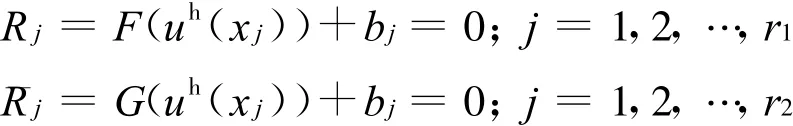
(1)离散微分方程的过程直接,实现其离散方程的算法简洁;

(2)是真正的无网格法,只需要在各节点处计算形函数及其导数,不需要进行数值积分,易于实现,计算效率高;

(3)位移边界条件很容易实现,不需要特殊处理;

(4)需要在各节点处计算形函数的二阶导数;

(5)系数矩阵一般是稀疏非对称的;

(6)在某些情况下,离散代数方程是病态的,其解不稳定,且精度差.

2 导数边界条件处理技术

配点法应用于实际的关键问题是导数边界条件的存在.当边界条件均为Dirichlet型时,用配点型无网格法可得到微分方程的精确结果,但存在任意导数边界条件时,其结果将显著恶化且不稳定.这是由于采用无网格近似函数进行函数逼近时,在边界处对函数的二阶导数逼近误差很大[6].有许多用于在配点型无网格法中施加导数边界条件的方法,其中常用的5种为

(1)直接配点法

通过简单的配点对导数边界进行离散而得到不同于控制系统方程的一组单独方程,即对导数边界条件不作特殊处理.

(2)虚点法

沿导数边界在问题域的外侧增设一组虚点.在此条件下对于每个导数边界节点可得到两个方程:一个方程对应导数边界条件,另一个对应微分方程.

(3)Hermite型配点法

对导数边界节点利用附加的导数变量施加导数边界条件.

(4)规则网格法

该方法沿问题域的导数边界内侧布置一层或数层规则分布的节点.对这些节点采用FDM的标准差分方案,即采用与标准FDM一样的处理方法施加导数边界条件.

(5)加密导数边界附近的节点

本文针对求解Helmholtz问题的基于点插值的配点型无网格法[6],对具有导数边界条件的Helmholtz问题采用积分插值的方法处理导数边界条件.对3个节点的插值法构造形函数的配点法,采用积分插值法1,其过程为设Helmholtz问题的导数边界条件

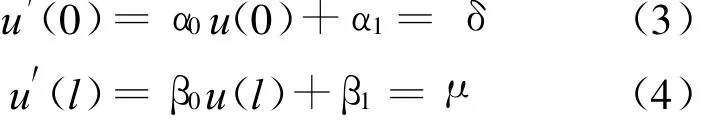
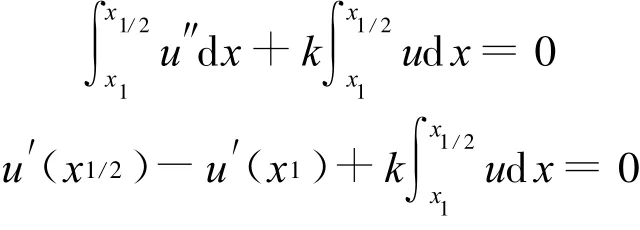
对u′(x1/2)采用中心差商采用左矩形公式得

于是有

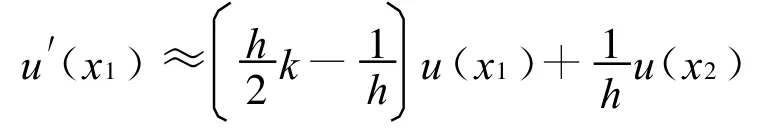
那么对式(3)可以用下式离散:

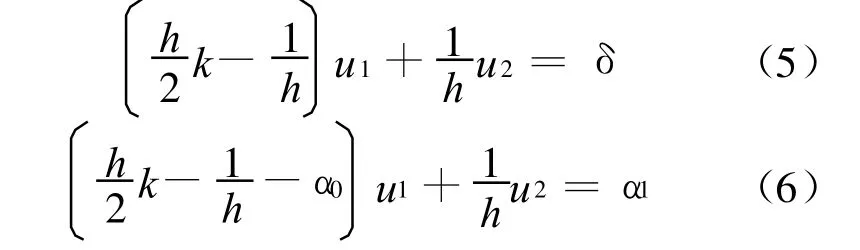
其中u1、u2分别为u(x1)、u(x2)的近似值.

对边界条件(4)在区间[xN-1/2,xN]上构造积分守恒式,采用同样的方法处理.

对于用5个节点插值构造形函数的配点法,采用的积分插值法2,其过程如下:在[xN-4,xN]上Helmholtz方程满足积分方程

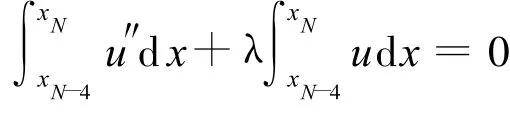
从而有

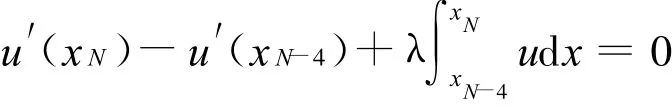
即得

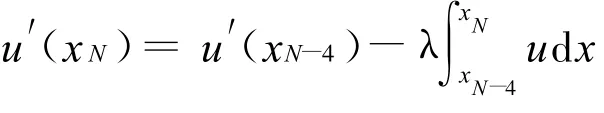
对其用New ton-Cotes公式近似,即

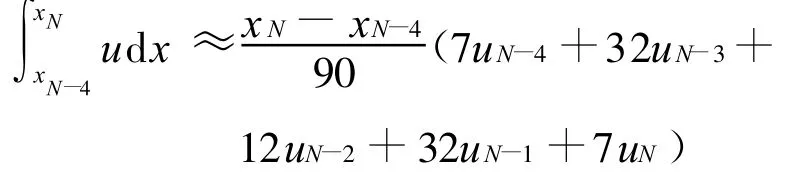
因此,导数边界条件(4)可以近似表示为

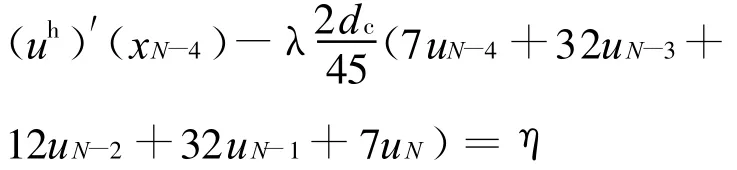
其中dc为节点间距,对u′(xN-4)用已求得的包含节点xN-4的函数近似式uh(x)的导数近似.对边界条件(3),在区间[x1,x3]上构造积分方程,采用同样的方法处理(但对散乱节点的情形,导数边界节点要进行规则化处理).

规则节点法是在导数边界处安排3个规则分布的节点xN-2、xN-1、xN.使用如下有限差分算法计算导数边界节点的一阶导数

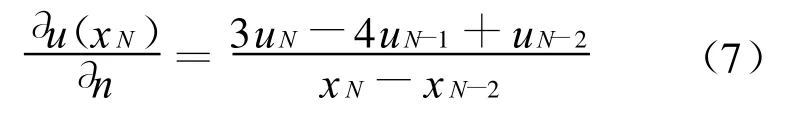
利用上式代替导数边界条件得到离散代数方程组.

在Hermite型近似中,将增设导数变量作为附加的自由度,对于内部节点,如果其局部支持域中不含导数边界节点,则采用传统的无网格形函数,形成配点方程.如果其局部支持域中包含导数边界节点,则采用如下的Herm ite型近似式

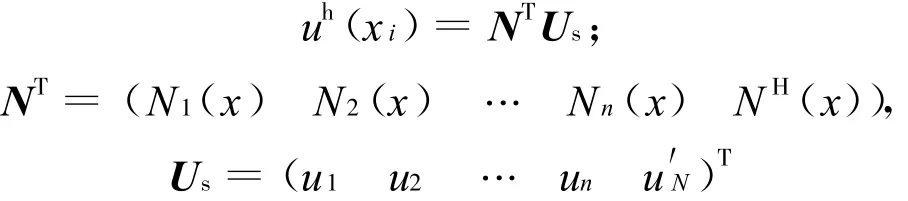
式中:N为由Hermite型近似得到的形函数向量,NH(x)为与导数自由度u′N有关的形函数.对采用基于三角函数点插值的配点型无网格法,Hermite型近似式的形成过程如下:

对局部支持域中含有导数边界节点的计算点x处的函数近似为

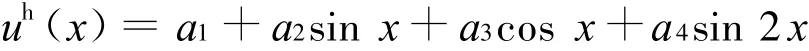
如采用5个节点插值构造形函数,则为

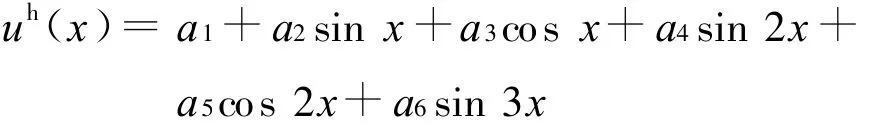
为确定式中的系数a1、a2、a3、a4,可用通过支持域中的3个节点的函数值的插值以及等于导数边界节点的导数值而确定.即对局部支持域中的3个节点(包括导数边界节点)可得到

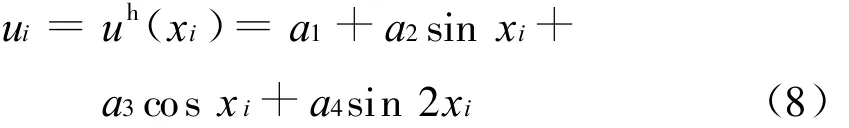
对式(8)求导后可得到边界方程

联立式(8)、(9)求出系数a1、a2、a3、a4就可以得到式(7)的形式.

3 数值算例

下面通过数值算例揭示各种不同导数边界条件处理技术对计算精度的影响.设带有Neum ann条件的一维Helmholtz问题为

为揭示导数边界条件对计算精度的影响,平均相对误差e定义如下:

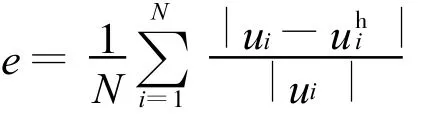
其中N为节点数;ui为理论解;uhi为数值解.相对数值误差范数的h收敛率R(e)定义为

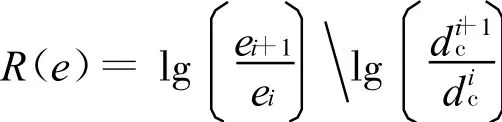
其中为平均节点间距.

表1、2列出了不同的插值方案和几种不同的处理导数边界条件的方法求解Helm ho ltz问题所得到的误差结果.各种不同方法的h收敛率情况如表3所示.

由表1、2、3可得到如下结论:

(1)如果Helmholtz问题仅有Dirichlet边界条件,用点插值配点法可得到非常理想的结果,其误差很小.用11个规则节点离散问题域,对三节点插值的模型e≈0.080600%,对五节点插值的模型e≈0.000027%.

(2)Neumann条件的存在将导致较大的计算误差.如果不对Neum ann条件采用特殊的处理方法(直接配点法),对三节点插值的模型e≈1.580000%,对五节点插值的模型e≈0.000833%,即误差分别放大约20和31倍.因此,直接配点法虽然既简单又直接,但是它仅对Dirichlet边界条件的问题有效,对存在Neum ann条件的问题通常不稳定或不精确.

(3)对Neumann条件进行特殊处理有助于改善解的精度.

(4)Hermite型配点法和积分插值法对两种模型均可得到精确而稳定的解.对三节点插值的模型两种方法误差放大约为4倍.对五节点插值的模型两种方法的数值误差几乎与仅有Dirichlet条件产生的误差相等.但Hermite法增加了自由度从而增加了计算成本.

(5)虚点法对两种模型的处理也能得到较好的结果.然而它使得方程数增加并需要额外的网格划分.

(6)规则网格法对五节点插值模型的效果比直接配点法差.这是因为式(8)采用接近导数边界的3个节点处理其导数边界,而其误差大体上由边界条件所引起的较大误差所决定,尽管增加了内节点的插值阶数,但是其精度将不会改善.

(7)虽然各种方法的精度各不相同,但它们的收敛率几乎相等.三节点插值方案的收敛率约为2,五节点为4～5.

表1 三节点插值不同方法所得到的误差结果Tab.1 The resu lt errors of differentmethods with 3 point interpo lation

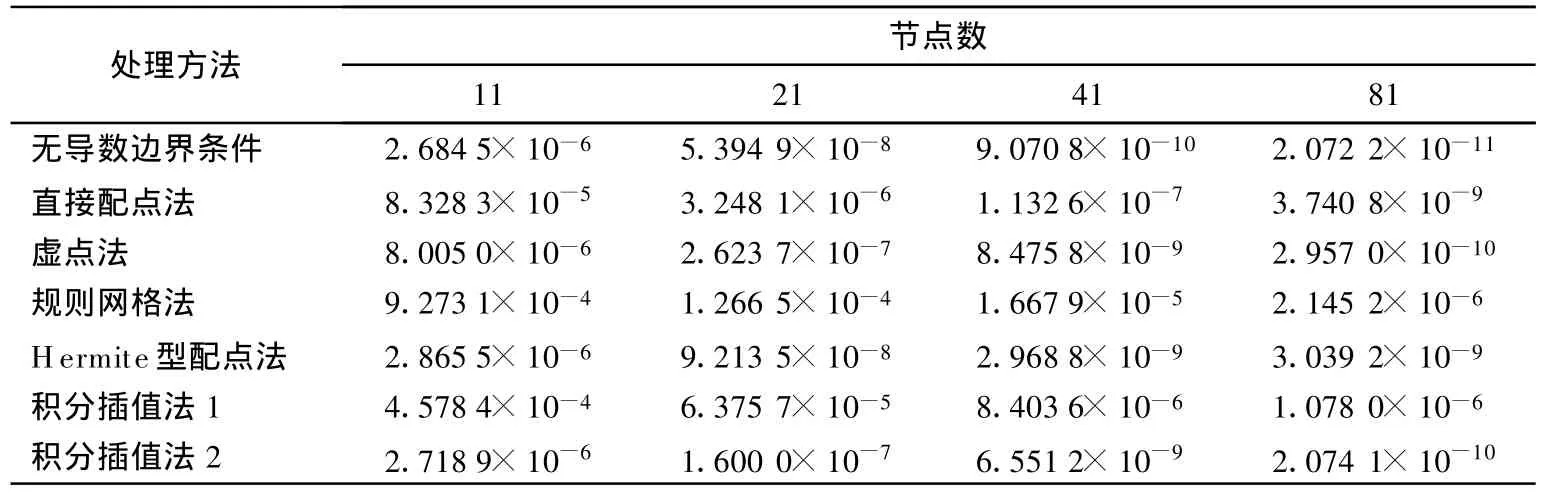
表2 五节点插值不同方法所得到的误差结果Tab.2 The resu lt errors of differentmethods with 5 point interpo lation

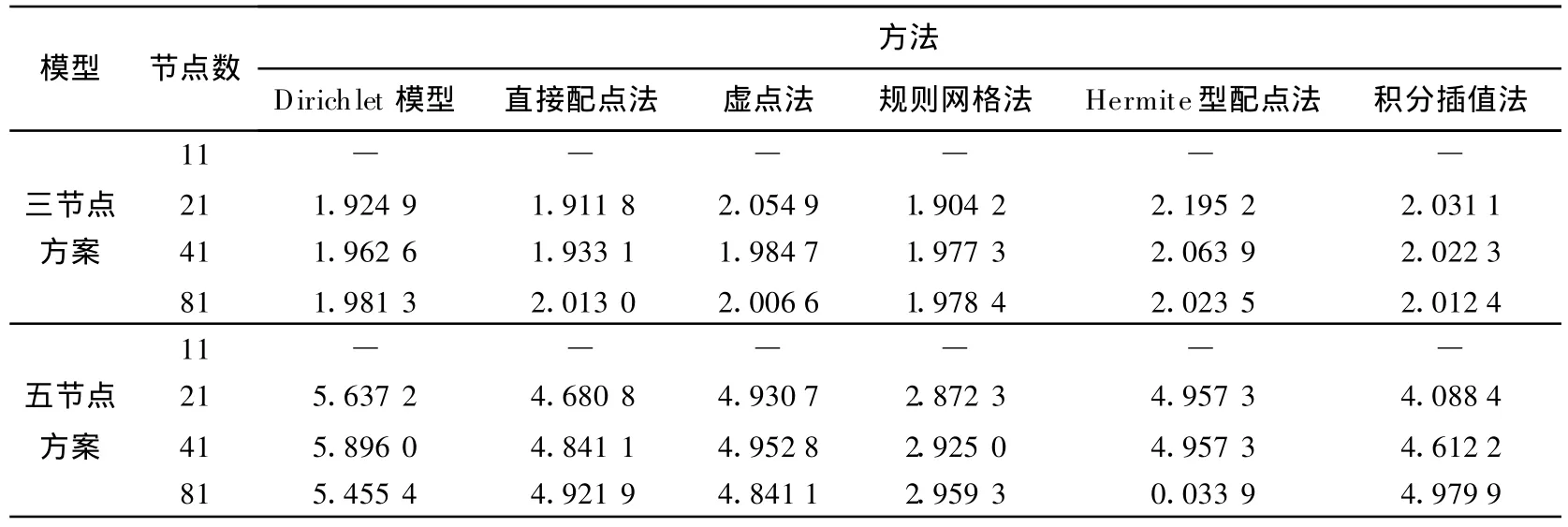
表3 不同方法所得的h收敛率Tab.3 The h rate of convergence of differentmethods

4 结 语

本文在对基于三角函数点插值的配点型无网格法解Helmholtz问题研究的基础上,分析了导数边界条件是影响配点型无网格方法求解精度的真正元凶,对几种流行的导数边界条件处理技术进行了详细的探讨.对一维问题的导数边界条件提出了操作简单、计算精度高,不增加自由度的较理想的解决方案——积分插值法.并通过具体的数值例子说明了它的优越性.

[1]BELYTSCHKO T,LU Y Y,GU L.Element free Galerkin methods[J].International Journal for Numerical Methods in Engineering,1994,37(2):229-256

[2]LIU W K,JUN S,ZHANG Y F.Reproducing kernel particlemethods[J].International Journal for Numerical M ethods in Fluids,1995,20(8-9):1081-1106

[3]LUCY L B.A numerical app roach to the testing o f the fission hypothesis[J].The Astronom ical Journal,1977,8(12):1013-1024

[4]CHEN W.Symmetric boundary knot method[J].Engineering Ana lysis with Boundary Elements,2002,26(6):333-343

[5]张 雄,刘 岩.无网格法[M].北京:清华大学出版社,2004

[6]LIU G R,GU Y T.无网格法理论及程序设计[M].3版.王建明,周学军,译.济南:山东大学出版社,2007