基于UD矩阵分解的模糊建模算法及收敛性分析
王 佳, 王宏伟, 顾 宏
(大连理工大学控制科学与工程学院,辽宁大连 116024)
0 引 言
实际过程中存在的大量非线性系统,有时可以用线性模型描述,但这仅仅是一种近似或者只限于在某一范围内成立.一般来说,在整个操作域中用非线性模型才能对非线性过程给予适当的描述.基于模糊集合的模糊模型,利用模糊推理规则描述复杂、病态、非线性系统是一种有效方法.模糊聚类是常用的模糊模型结构确定方法,其中心思想是设定合理的聚类指标,根据该指标所确定的聚类中心可使模糊输入空间达到优化.模糊聚类法主要有模糊C均值方法及各种改进的模糊C均值方法[1~3].对于各种模糊聚类算法而言,需要解决以下几个问题:(1)聚类规则数一般是预先给定的,不能说明规则数多少对于描述系统是最优的;(2)聚类过程计算量较大,不适合于在线建模与控制;(3)聚类结果往往受初值等参数影响较大,容易陷入局部极小值点;(4)在基于模糊模型的建模过程中,如果聚类效果不好,则使各类之间存在线性相关性;(5)在工程实际应用中,噪声和干扰的存在,以及变量之间的耦合,使输入变量之间存在线性相关性[4、5].如何找到这些规则,化简规则,压缩模糊模型的输入空间是模糊建模的关键问题.
本文提出一种可用于非线性系统模糊建模中结构确定和参数估计的新方法.首先,通过GK模糊聚类确定模型结构.然后,通过目标函数与参数估计一起进行递推计算,进而实现对模糊模型结构简化,删除冗余规则,同时进行模型参数的估计,并证明提出算法的收敛性.最后,将M ackey-Glass混沌时间序列预测作为仿真实例,分别将本文的方法与其他文献中提出的方法进行比较,以证明本文方法的有效性.
1 模糊模型结构的确定
一个多输入多输出(M IMO)系统P(U,Y),U∈RM,Y∈Rq,可以分解成q个多输入单输出(MISO)系统.这里仅讨论M ISO系统,形式如下:

其中 Ri表示第i条规则;Z是输入向量,Z=(x1x2 …xM)TRM;Zi是第i条规则的中心向量,是第i条规则的隶属度函数,μi(k)表示第k个样本在第i条规则里的隶属度,满足为总规则数;θi是后件参数.
模型(1)的整体输出为

式中 :H=(φ1 φ2 … φc),φi=(μi(1)μi(2) … μi(N))T,i=1,2…,c,简记为H=(μi(k))N×c, Ψ=(θ1 θ2 … θc)T.
根据最小二乘法有

其中y(k)表示第k次实际输出,Y=(y(1)y(2) …y(k) …y(N))T.
2 模糊模型的简化和数据压缩
2.1 问题的提出
若用最小二乘法解式(3)超定方程求解模型的参数,需要解决以下几个问题:
(1)在工程实际应用中,噪声和干扰的存在以及变量之间的耦合,使输入变量之间存在线性相关性;
(2)在基于模糊模型的建模过程中,往往采用聚类的方法,但是如果聚类效果不好,易使各类之间存在线性相关性;
(3)为了提高建模精度而增加变量数量时,Ψ、H、Y的维数也相应增加,将涉及到如何降低在求解线性方程组时由于计算机有限字长而引起的计算误差.计算误差在建模中会引起建模精度下降.理论上收敛的算法在实际应用中可能会发散.
对于(1)、(2)两个问题,会使HTH形成奇异矩阵,即使不是奇异矩阵,但由于HTH存在着近似为零的特征值, Ψ的估计变得不可信,因此必须对模糊模型进行简化.对模糊模型(1)来说,它的参数向量总含有一些对建模贡献非常小的元素,可以近似地认为其值为零.如果在辨识参数向量之前,确定出这些元素所在的位置,并将它们删除,然后重构模型(1),这样既降低了式(1)的维数,又有利于降低计算量和提高辨识精度,同样也就解决了问题(3).
2.2 基于目标函数的模型结构和参数确定
对于模糊模型(1)而言,如何确定规则数,保留重要规则和删除对建模贡献小的规则,成为模糊建模的关键问题.为了解决这个问题,首先分别设定不同的规则数m(m 如果Jm小,表示拟合得好,设定的规则数比较合适;如果Jm大,说明拟合得不好,设定的规则数不符合待辨识系统.一般地,目标函数的值总是随阶次的增大而减小,不过当设定的阶等于或大于系统的真实阶后,目标函数的值随阶次的增大而明显下降,这就是所谓的“过拟合”.下面介绍基于目标函数的模型结构与参数一体化确定方法. 对于模型(1),假设 φ1,φ2,…,φm已通过分析方法选入模型,现在考虑 φm+1,φm+2,…,φc的选入与剔除问题. 根据目标函数式(4),有 若将φm+1选入模型,则有 式中: θm+1(l+1)为待估计的参数;φm+1=(μm+1(1) μm+1(2) … μm+1(N))T;l为模型的优化次数. 对矩阵HTmHm进行UD矩阵分解,则有 从而得出 另外,还有 由式(6)和(11)可得 此时目标函数为 上式可简化为 对于事先选定的Jm in,若ΔJ≥Jm in则选入φm+1,否则剔除. 将2.2的公式推导过程整理,得到递推辨识方法如下: Step 1 首先,采用GK模糊聚类算法确定μi(k)(i=1,2,…,c;k=1,2,…,N),则所有待选变量为 φi(i=1,2,…,c),φi=(μi(1) μi(2)… μi(N))T. Step 2 在φi(i=1,2,…,c)中,根据经验选取其中某一个φi作为初始变量,并对模型中的有关参数进行辨识,当辨识步数足够时,再进行模型辨识. Step 3 利用式(12)分别求得 θm+1、 Ψm(l+1),由式(15)计算 ΔJ1.若 ΔJ1 Step 5 利用式(12)分别求得 θm+2(l+2)、Ψm+2(l+2),由式(15)计算 ΔJ2.若 ΔJ2 依此下去,若连续c次剔除所选量,则停止选择,即可得到系统模型. 定理1 对于模型(1)的辨识递推算法,式(12)给出的参数估计值 Ψ是一致收敛的. 证明 若将 φm+1选入模型,考虑 Ψm(l+1)对真值的收敛性问题. 根据式(7)和(9)可得 另外,根据式(6),可得 这样得到 根据式(12),可得 根据式(16)和(18),上式变为 令 Ψm为结构中前m个参数的真值,那么真值 Ψm与参数估计值 Ψm的误差为 Ψm(l)=Ψm-Ψm(l), Ψm(l+1)= Ψm- Ψm(l+1),这样就有 假设系统的实际结构为m+L,模型的真实参数为θi(i=1,2,…,m+L),这样系统可以表示为 那么,式(20)变为 式(23)经过整理有 其中m(l+1)为对于误差 Ψm(l)的无关项. 下面讨论差分方程(25)形如x(k+1)=A(k)x(k)的稳定性问题.设矩阵特征值为λ,则下式成立: 其中X是非零的特征向量,进一步可得 易知Pm、Qm都是正定阵. 对于式(12)左边是正定的,dm+1必须满足dm+1>0,对所有非零向量X,式(27)两边的λ、1-λ必须同号,即可见矩阵的特征值λ一定是0<λ<1的,这意味着式(25)一定是稳定的,即收敛性得证 . 本文将M ackey-Glass混沌时间序列预测作为仿真实例,以证明所提出方法的有效性.混沌时间序列可由时滞微分方程得到 Mackey-G lass系统预测的目的是根据t时刻以前的一组数据x(·),去预测x(t+Δt),其中 Δt为预测时间步幅.预测方法是令Δt为时滞参数,取D个点 ,即{x(t-(D-1)Δt),…,x(t-Δt),x(t)}去预测将来时刻x(t+Δt).若n为整数,仿真研究的任务是利用模糊模型构造函数.取τ=17,Δt=6,选1000对样本数据,即其中,前4个变量数据作为输入,最后一个变量数据作为输出.前500对数据当作训练数据,其余500对数据作为测试数据以验证辨识模型的有效性.取30条模糊规则作为初始规则数,针对上述已建立的含有30条模糊规则的系统,取 ΔJ=0.1,最后经过优化后得到的规则数为16. 经过规则优化后,得到的模糊模型输出和实际样本的均方差为0.0052,图1~4给出了仿真曲线. 文献[6~10]针对上述混沌系统进行了建模研究,将本文方法与它们进行比较,可看出本文方法优于文献提出的方法,见表1. (1)文献[7]结果均方差为0.0016,小于本文方法的0.0052.但是,其方法参数为104个,远大于本文方法中的16个.另外,文献[7]运行计算时间需要20 min,而本文方法只需3m in. (2)文献[8~10]也分别提出了不同建模方法,但是在输入变量个数、规则数和参数的数量综合指标方面,本文方法明显好于文献[8~10]中的方法. 图1 训练数据的模糊模型输出与实际输出Fig.1 The fuzzy mode l output and the actua l output for training data 图2 训练数据误差曲线Fig.2 The error curve of the training data 图3 测试数据的模糊模型输出与预测输出Fig.3 The fuzzy model output and the forecast output for test data 图4 测试数据误差曲线Fig.4 Theerror curve o f the test data 表1 本文模型与其他模型的比较Tab.1 The comparison of the model in this paper and othermodels 针对模糊模型的结构辨识和参数估计问题,提出了基于目标函数的建立非线性系统的模糊模型的方法.通过目标函数与参数估计一起进行递推计算,实现了对模糊模型结构简化,删除冗余规则,得到模型结构的同时进行了模型参数的估计.结构确定过程中采用了UD矩阵分解方法,大大降低了计算量. [1]HAN M in,SUN Yan-nan,FAN Ying-nan.An imp roved fuzzy neural netw ork based on T-S model[J].Expert Systemswith App lications,2008,34(4):2905-2920 [2]DU H ai-ping,ZHANG Nong.Application of evo lving Takagi-Sugeno fuzzy model to non linear system identification[J].App lied Soft Com puting,2008,8(1):676-686 [3]潘天红,李少远.基于模糊聚类的PWA系统的模糊辨识[J].自动化学报,2007,33(3):327-330 [4]刘士荣.神经模糊系统的若干问题研究[D].上海:华东理工大学,2000 [5]孙富春,刘华平,孙增圻.非线性系统神经模糊自适应控制的问题与策略[J].清华大学学报(自然科学版),2003,43(4):470-474 [6]SCHURTER K C,ROSCHKE P N.Fuzzy modeling of amagnetorheological damper using ANFIS[C]//IEEE International Con ference on Fuzzy Systems.Piscataw ay:IEEE,2000:122-127 [7]K IM D,KIM C.Forecasting time series with genetic fuzzy p redictor ensemble[J].IEEE Transactions on Fuzzy Systems,1997,5(4):523-535 [8]KUKOLJD.Design of adap tive Takagi-Sugeno-Kang fuzzy models[J].App lied Soft Computing,2002,2(2):89-103 [9]DE SOUZA F J,VELLASCO M M R,PACHECO M A C.H ierachical neuro-fuzzy quad tree models[J].Fuzzy Sets and System s,2002,130(2):189-205 [10]WANG L X,M ENDEL JM.Generating fuzzy rules by learning from examp les[J].IEEE Transactions on System s,Man,and Cybernetics,1992,22(6):1414-1427
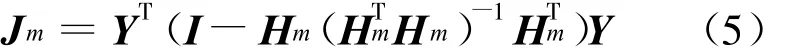


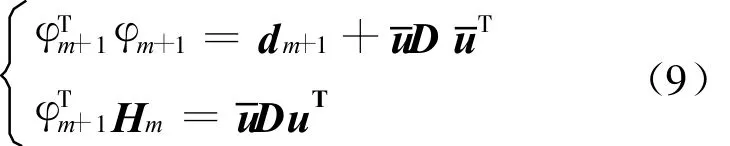
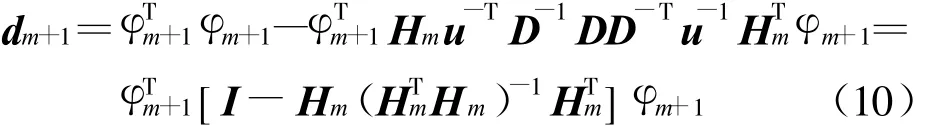
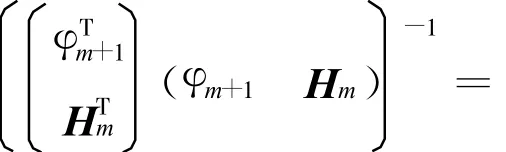


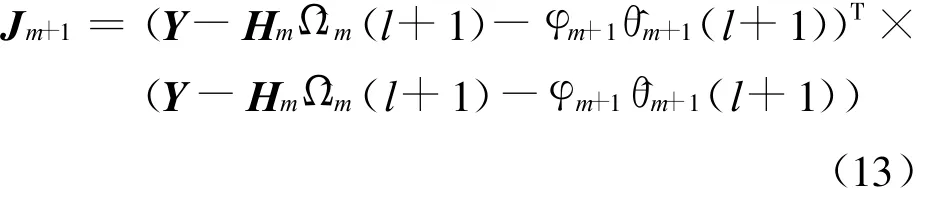


2.3 结构和参数一体化在线辨识算法
3 算法收敛性分析













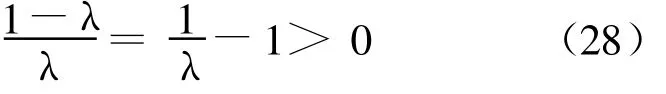
4 仿真实例

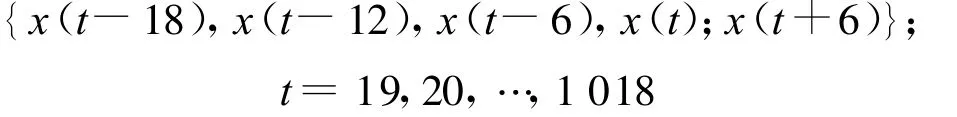





5 结 语

