α稳定分布噪声条件下TVAR模型参数估计

邱 天爽, 栗 娜, 里红杰,2

(1.大连理工大学电子信息与电气工程学部,辽宁大连 116024;

2.大连工业大学信息科学与工程学院,辽宁大连 116034)

0 引 言

实际中的随机信号许多是非平稳非高斯的,长期以来囿于理论的发展,只好将其简化为平稳高斯随机问题,其结果当然令人不甚满意.许多随机信号或噪声往往具有显著的尖峰脉冲特性,使得其统计特性显著偏离高斯分布,其概率密度函数的衰减过程比高斯分布要慢,从而造成了显著的拖尾.通常用α稳定分布模型来描述这类具有显著尖峰脉冲状波形和较厚概率密度函数拖尾的随机信号,α越小拖尾越厚,脉冲性越强.由于α稳定分布信号不存在有限的二阶和二阶以上矩,在高斯条件下基于二阶矩理论的信号处理算法在α稳定分布条件下性能退化[1].因此需要根据信号噪声的特点研究出新的信号处理方法.例如在实际应用中,对于信号中突发性的野值干扰,当采用范数为2的最小均方误差准则时,平方的作用放大了野值的影响,从而使对系统的自回归(AR)估计产生严重影响.如果选用较小的范数,则会对较大误差有一定的抑制作用,从而使估计结果的稳健性更好.

本文主要结合非平稳信号的 TVAR模型描述以及α稳定分布条件下信号处理的最小p范数(LPN)方法,给出一种估计非平稳信号TVAR模型时变参数的最小p范数方法.

1 非平稳随机信号的时变AR模型

时变参数模型法是近年来应用于非平稳随机信号分析与处理的一种新方法.这种方法通常用具有时变参数的AR模型和自回归滑动平均(ARMA)模型来表征非平稳随机信号,将时变参数假设为一组基时间函数的线性组合.由于任何MA和ARMA模型都可以用无穷阶的AR模型来表示,并且AR模型计算比较简单,信号处理中常用AR模型来表征信号.时变参数模型法的优点在于将一个线性非平稳问题转化为一个线性时不变问题,而且与假设在一段时间间隔上信号是平稳的参数估计方法相比,时变参数模型法可以进一步提高参数估计的精确度[2].

设零均值、N阶时变参数自回归(TVAR)模型[3 、4]为

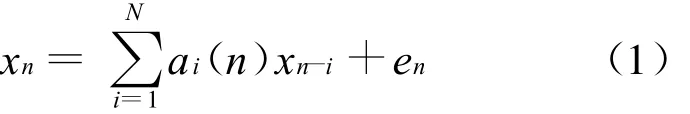
式中:en为平稳白噪声过程,假设时变参数{ai(n),i=1,…,N}是一组基时间函数的线性组合,

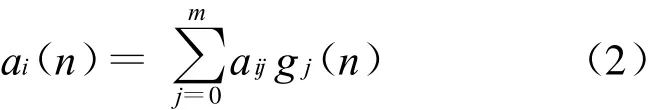
式中{gj(n),j=0,…,m}是一组基时间函数,m称为基的程度.

由以上可以看出:N个时变参数被一组定常参数{aij}所代替,这种方法也可以称为坐标方法.当参数被看成是以{gj(n),j=0,…,m}为基的一个时间函数时,它是由xn的轨迹坐标构成的.这样就将一个标量过程替换成向量过程,从而把一个线性非平稳问题转化为一个线性时不变问题.

2 TVAR模型的最小p范数估计

2.1 AR SαS 过程

通常认为AR、MA、ARMA过程的激励en是独立同分布(i.i.d.)的高斯过程,这种假设在许多情况下是合理的.但是,在某些场合,高斯激励的线性模型就不再适用,比如水文数据、气象数据以及具有很大的瞬时尖峰脉冲的数据,包括股票市场价格、电话信号和一些生物医学信号等.这类尖峰脉冲信号的分布比高斯分布有更厚的拖尾,而且具有无限方差.这时,原有的基于二阶统计量的分析方法不再适用,需要新的不受有限方差限制的参数模型方法[5].

最常用的具有无穷方差的线性模型是自回归(AR)SαS过程,一个ARSαS过程xn可表示为

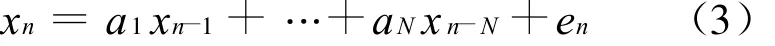
这里en是一个特征指数为α,分散系数为 γ的i.i.d.的SαS分布过程.

2.2 TVAR模型时变参数的最小p范数估计方法

对于稳定过程的线性估计问题,由于没有有限方差,最小均方误差(MMSE)准则不再适用,但是MMSE准则的概念可以推广到稳定分布过程.特别地,最小分散系数(MD)准则可以用于讨论稳定过程的线性理论.在MD准则下,一个SαS随机变量在观测线性空间的最佳估计是使估计误差的分散系数最小.一个稳定随机变量的分散系数具有和方差同样的地位和作用.分散系数越大,远离中值的稳定随机变量的样本越多.因此,通过分散系数的最小化,可以使估计误差的平均幅度达到最小[6].

设一个非平稳ARSαS过程为

式中:en为特征指数为α、分散系数为γ的i.i.d.的SαS分布过程 .令

则式(4)可以写成如下形式:

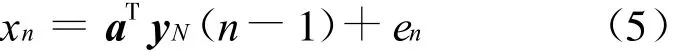
要估计TVAR模型的时变参数,目标就是使式(6)最小化:

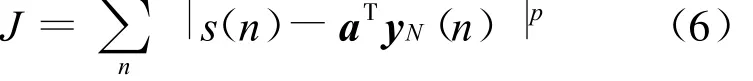
其中s(n)是期望信号.对式(6)相对于系数矢量a的每个元素求偏导,并令其为0,得到

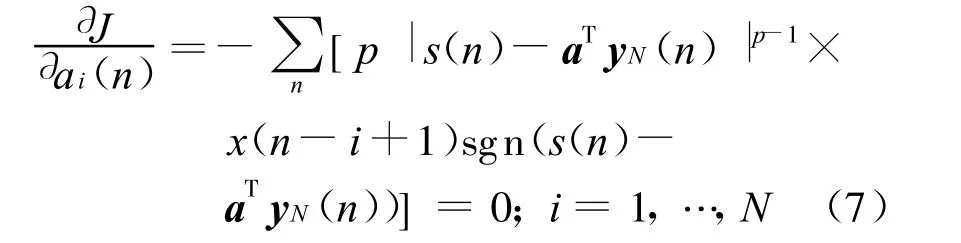
定义残留矢量为r,其中第n个元素

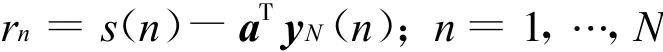
这样,式(7)可简化为

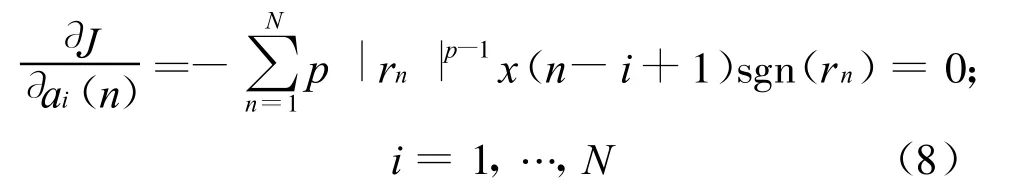
由于sgn(rn)=rn/|rn|,式(8)等价于

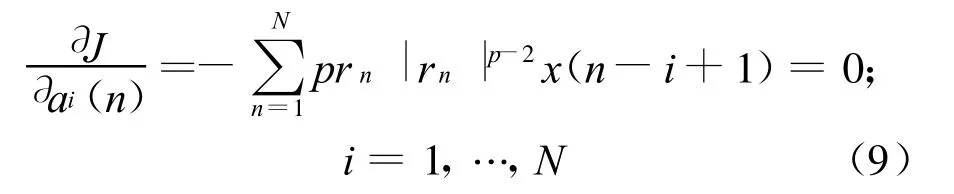
式(9)等号两边同除以p,可以消去p.同时定义一个加权对角阵

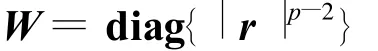
用矩阵形式来表达式(9),有

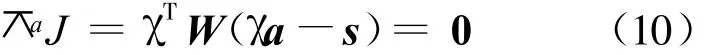
这里

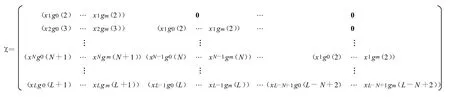
求解式(10)得

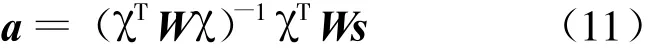
该式是加权最小二乘问题.然而,这里a是W的函数,而W又是a的残留函数.因此,这个公式没有解析解,其迭代解法如下:

这里,a(k)是TVAR模型第k步迭代的参数矢量,‖·‖(p)表示lp范数.

3 仿真实验

为了研究上述算法的性能,对一 TVAR(2)模型的时变参数进行了估计,并对用本文中最小p范数(LPN)方法得到的估计结果与用传统递推最小二乘[7](RLS)法得到的估计结果进行了比较.

常用的基时间函数有很多种,本文采用傅里叶基时间函数,形式如下:

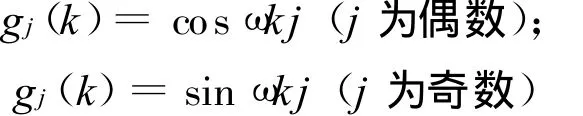
其中j=0,1,…,m,m越大,模型描述非平稳信号特性越准确,但运算量也随之显著增加,综合考虑这两点因素,本实验中基的程度取m=2.

实验中要讨论的二阶时变AR过程如图1所示,可以用式(12)表示:

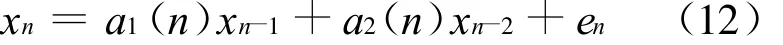
其中a1(n)=0.1+0.5sin ωk+0.7cos 2ωk,a2(n)=-0.3-0.7sin ωk-0.2cos 2ωk,当en是i.i.d.高斯时间序列时信号xn如图1所示,当en是i.i.d.SαS时间序列时xn如图2所示.

从图中可以看出,图2所示的SαS过程不同于图1所示的高斯随机过程,信号中存在较大的尖峰脉冲.对图2所示信号的α参数进行估计,得到α=1.03.

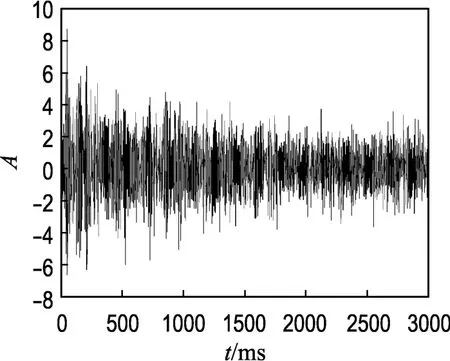
图1 二阶TVAR高斯过程Fig.1 Second-order Gaussian process with TVAR model

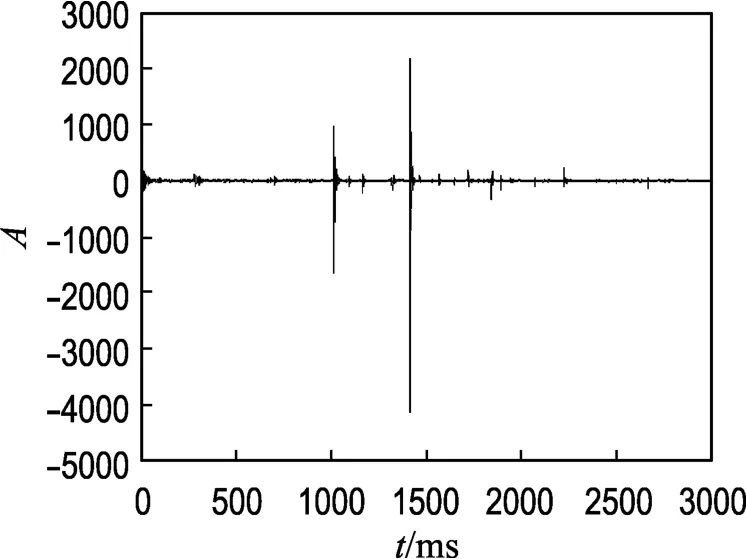
图2 二阶 TVAR SαS过程Fig.2 Second-order SαS processw ith TVARmodel

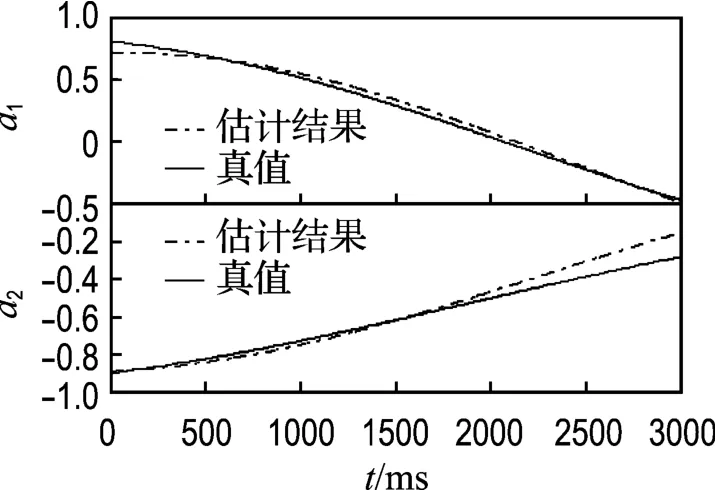
图3 高斯噪声条件下LPN估计结果Fig.3 Estimation using LPN algorithm underGaussian noise conditions

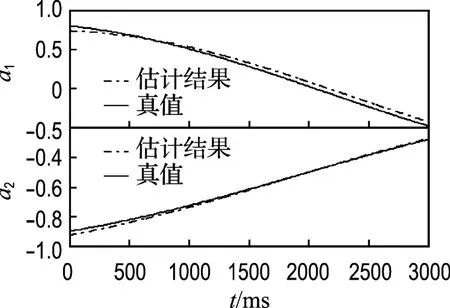
图4 高斯噪声条件下RLS估计结果Fig.4 Estimation using RLS algorithm under Gaussian noise conditions

分别用最小p范数(LPN)方法与递推最小二乘(RLS)法对图1和2所示信号进行TVAR模型参数估计,在高斯条件下即对图1所示信号估计得到的结果如图3和4所示,在α稳定分布条件下即对图2所示信号估计得到的结果如图5和6所示.从图中可以看出,在高斯条件下,两种方法都可以得到比较准确的估计结果.在α稳定分布情况下,本文的LPN方法可以得到比较准确的TVAR模型的时变参数;而RLS方法得到的估计结果存在较大误差,基本不能给出模型参数随时间的变化情况.两种方法在两种条件下的误差情况如表1和2所示,其中误差均值和误差功率计算公式如式(13)、(14).实验结果说明,在高斯条件下适用的RLS算法在α稳定分布条件下性能退化;而LPN算法既适用于高斯条件又适用于α稳定分布条件,比RLS算法具有更广泛的适用性.

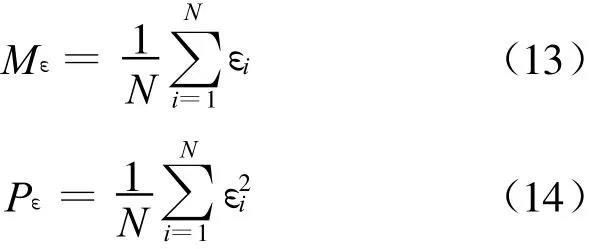
其中εi(i=1,2,…,N)为各时刻的估计误差.

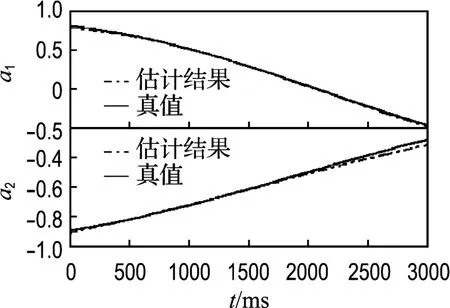
图5 α稳定分布噪声条件下LPN估计结果Fig.5 Estimation using LPN algorithm under α-stable distribution noise conditions

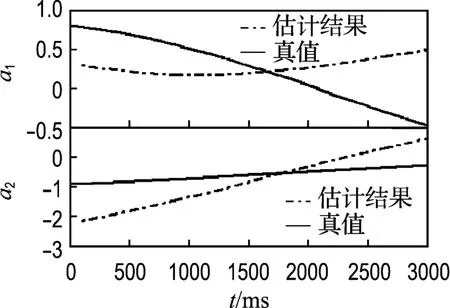
图6 α稳定分布噪声条件下RLS估计结果Fig.6 Estimation using RLS algorithm under α-stab le distribution noise conditions

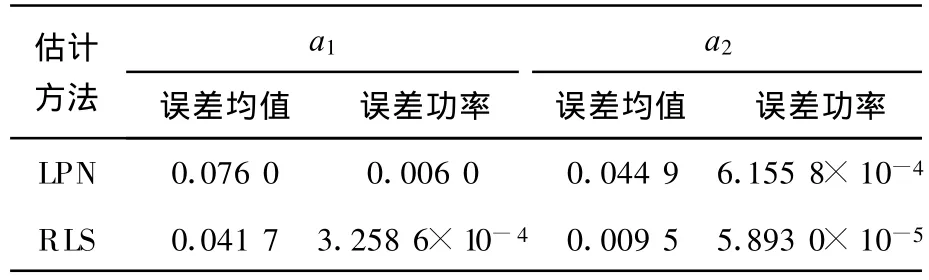
表1 高斯噪声条件下LPN方法与RLS方法结果误差比较Tab.1 Error comparison of LPN algorithm and RLS a lgorithm under Gaussian noise conditions

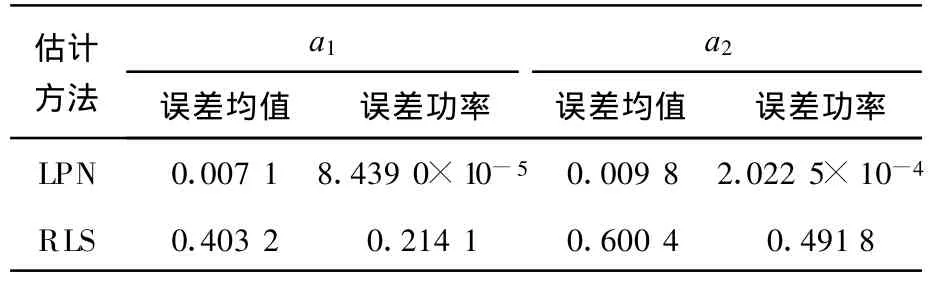
表2 α稳定分布噪声条件下 LPN方法与RLS方法结果误差比较Tab.2 Error com parison of LPN algorithm and RLS algorithm underα-stable distribution noise conditions

4 结 语

非高斯与非平稳信号处理是当前信号处理的研究热点,实际中很多信号都具有非高斯和非平稳特性,所以将这两个问题结合起来研究具有很重要的理论意义和实际价值.本文给出了一种用最小p范数法对非平稳信号TVAR模型时变参数进行估计的方法,这种方法既适用于高斯条件下非平稳信号TVAR模型的参数估计,又适用于非高斯α稳定分布条件下非平稳信号的参数估计,改善了传统的RLS方法仅适用于高斯条件的情况,较RLS方法具有更好的韧性.

[1]邱天爽,张旭秀,李小兵,等.统计信号处理—— 非高斯信号处理及其应用[M].北京:电子工业出版社,2004

[2]王宏禹.非平稳随机信号分析与处理[M].北京:国防工业出版社,1999

[3]ZHU Yong-liang, PAGILLA P R.Adap tive estimation of time-varying parameters in linear systems[C]//Proceeding of the American Control Conference.Piscataway:IEEE,2003:4167-4172

[4]SH EN M in-fen,SONG Rong,TING K H,etal.A method for identifying non-Gaussian parametricmodel with time-varying coefficients[C]//ICASSP 2003 Acoustics,Speech,and Signal Processing.Piscataw ay:IEEE,2003:629-632

[5]王文华,王宏禹.一种非平稳随机信号模型的时变参数估计算法性能研究[J].大连理工大学学报,1997,37(1):97-102(WANG W en-hua,WANG Hong-yu.An algorithm property analysis for time-varying parameters estimation o f nonstationary random signals model[J].Journal of Dalian University of Technology,1997,37(1):97-102)

[6]SODSRIC.Time-varying autoregressivemodeling for nonstationary acoustic signal and its frequency ana lysis[D].Pennsy lvania:The Pennsy lvania State University,2003

[7]冯大政,常冬霞,袁 莉.一种自适应全局最小p范数算法[J].电子学报,2001,29(12A):1848-1851