基于“小波包—模糊理论”的整流装置故障诊断系统的研究

旷永红，欧阳波，周 鹏

(1.湖南工程学院应用技术学院，湖南湘潭 411101;2.中南大学信息科学与工程学院，湖南长沙 410075）

基于“小波包—模糊理论”的整流装置故障诊断系统的研究

旷永红1，欧阳波2，周 鹏2

(1.湖南工程学院应用技术学院，湖南湘潭 411101;2.中南大学信息科学与工程学院，湖南长沙 410075）

针对电力、化工行业广泛使用的三相桥并联的同相逆并联整流装置，以整流变压器阀侧三相电流为诊断信号，提出了小波包－模糊推理实现故障诊断。首先利用小波包分析提取故障特征值，形成样本数据库;然后利用J散度、最大隶属原则方法实现待识别状态与样本状态的模糊识别。该方法通过实验，验证了其故障诊断的准确性。

同相逆并联;故障诊断;小波包分析;模糊推理

1 前言

在电力、化工、冶金等行业，电力整流设备通常用于生产工艺的关键流程之中，因电力整流设备故障而导致生产的中断则意味着重大的经济损失。电力整流装置故障主要以功率开关器件的断路和直通最为常见，需要实时监视诊断，并且故障只能以输出波形来诊断。

国内外研究现有的电力整流装置故障诊断方法主要有:谱分析法、直接检测法基于神经网络故障诊断方法。本文提出了基于小波包－模糊诊断的故障诊断方法，首先利用小波包变换对采集信号进行处理，提取在各种状态下的特征值;然后对特征值进行模糊处理，由最大隶属度原则得出待识别状态所属故障类型。该方法在实验条件下测试，验证了其故障诊断的准确性。

2 研究对象及研究方法探讨

大功率整流装置常采用同相逆并联拓扑结构，本文研究的是三相桥并联的同相逆并联系统。其特点是:两个整流桥组合在一起，系统相邻铜排电流，在任何瞬间均大小相等、方向相反，从而减少各部分线路电抗，并增加相间、臂间阻抗的对称度。

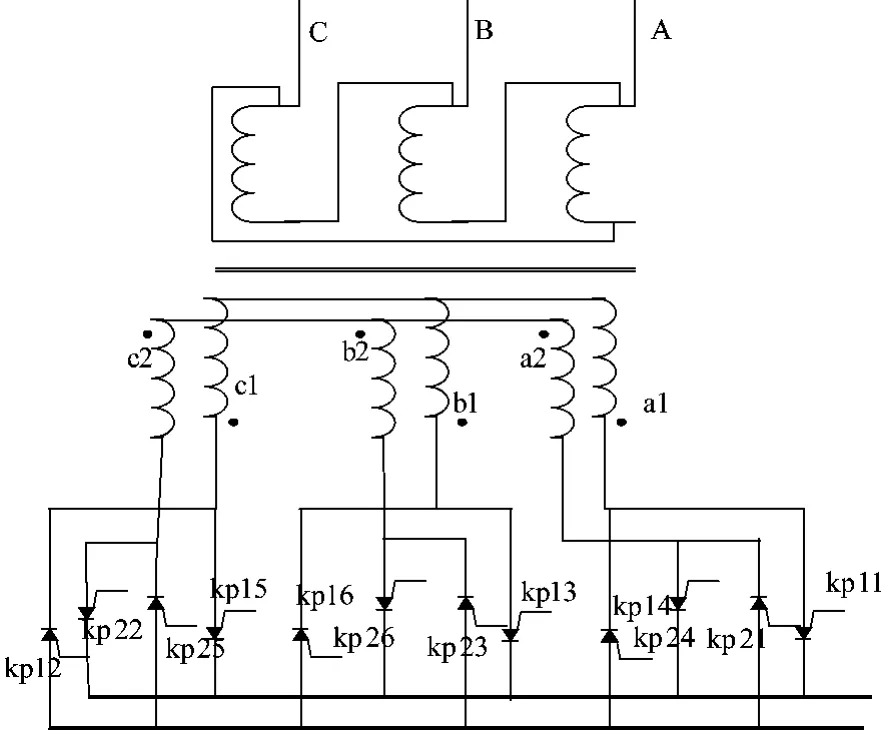
图1 同相逆并联结构图Fig.1 Structure of cophase counter parallel connection

图1［2］为两个三相桥式电路组成的同相逆并联系统，两个桥的三相交流电压互差180°，因此当图中右侧桥导电相序为 a1b1，a1c1，b1c1，b1a1，c1a1，c1b1时，相应地左侧桥的导电相序为 b2a2，c2a2，c2b2，a2b2，a2c2，b2c2，使得任何瞬间两桥相邻电路内的电流大小相等，方向相反，磁通最大限度被抵消。

检测信号采集:由仿真研究及文献［2］可知，由于两组桥处于并联方式，当一组出现故障时，负载两端的直流端电压不会发生明显变化，使得以直流输出电压和基于变压器网侧电流的研究方法不能适应这种结构的整流装置;但整流变压器阀侧两组三相支路能检测到故障信息，因此可以通过检测一组桥的三相电流来完成故障信息的检测。

本文采用待识别状态与已知状态的匹配方法来研究故障所属分类，因此样本数据库中系统的故障类型对故障诊断的准确性很重要。以三相桥式全控整流电路主回路开路故障为例，研究中故障的类型分为5大类:第一类:无晶闸管故障;第二类:有一个晶闸管故障，有六小类;第三类:接到同一相电压的两只晶闸管故障，有三小类;第四类:同一半桥中的两只晶闸管故障，有六小类;第五类:交叉两只晶闸管故障:有六小类。同相逆并联有两组三相桥，因此可分为第一组桥故障和第二组桥故障两组，本文研究暂只考虑一组桥出现故障情况，样本数据库中共计43种运行状态数据。

3 基于小波包-模糊诊断理论

故障特征的提取方法的研究是电力电子故障诊断技术的关键。本节讨论利用小波分析理论之一的小波包分析方法提取故障信号的特征值。它将频带进行多层次划分，对高频部分进一步分解，并能够根据被分析信号的特征，自适应的选择响应频带，从而提高时频分辨率。其分解遵循能量守衡原理［4］。当系统发生故障时，其输出信号能量的空间分布与正常系统输出相比会发生相应变化。

小波包分解算法如下:

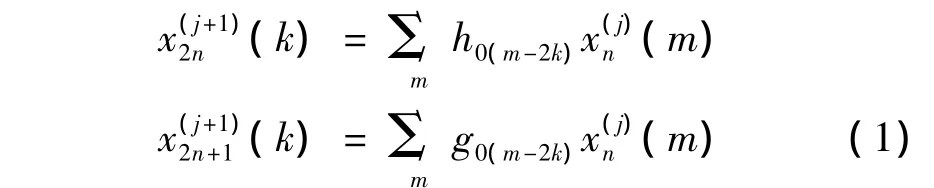
小波包重构算法如下:

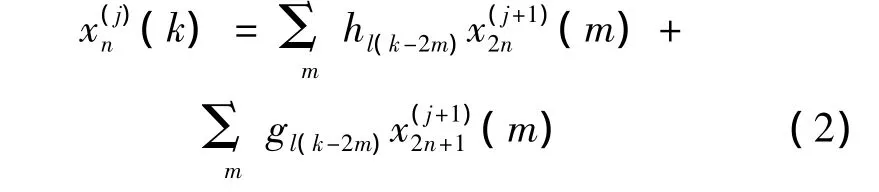
小波包分解实质上是对信号按照2n进行分解，一尺度分解得到高频和低频(D1和A1），二尺度分解在一尺度分解的基础上再分解得到四段(AA2、DA2、DA2、DD2）。依此类推，将信号分解为高、低频的频率段，并且每分解一次信号点数变为原来的1/2，称这些高、低频率段为小波包系数。

故障诊断其本质就是在分析设备异常现象的基础上，由症状推断出故障的原因。

本系统模糊诊断过程为:

(1）首先利用J散度来计算相似程度，J散度公式为:

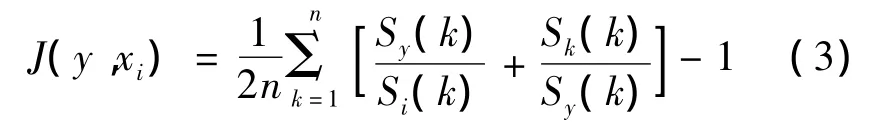
式中y(t）为待识别的信号，xi(t）为已知状态的信号，S(k）为信号的能量谱。当 J(y，xl）=min，则可说明y(t）所处状态与xl(t）所处状态是同一类。当Sy(f）=Si(f），即对同一个能量谱，J(y，xi）=0。

(2）然后求解模糊集合的隶属度。

由J散度指标可知，当其取最小值时，表明二状态的相似程度最大，因此可用偏小型函数来表示这种相似程度。能量谱J散度属于某状态的隶属函数，可用降半哥西分布表示为:

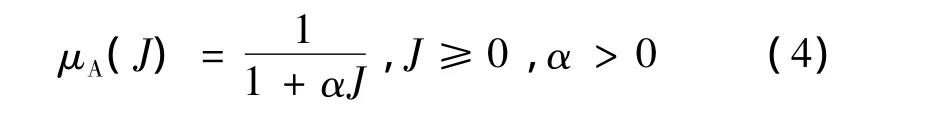
这样，距离值转化成［0，1］区间中的值，便形成了模糊处理中的隶属度。

(3）采用最大从属原则实现逻辑诊断，

最大从属原则定义为:设给定论域U上的n个模糊子集(模糊模式）A1，A2，...，An。其隶属函数分别是 μA1(u），μA2(u），…，μAn(u），使 μA1(u）=max(μA1(u），μA2(u），…，μAn(u）），则认为元素 u 应隶属于Ai，判决u归属Ai所代表的那个模式，叫做最大从属原则。

最大从属原则的缺点是当最大隶属度值与其它隶属度值之间的差距不大时难以作出可靠的诊断结论。为克服这个缺点，可采用连乘法。利用最大从属原则，则可以通过隶属度来进行故障的准确识别。

4 实验验证

(1）实验条件及分析

实验条件:整流变压器型号为 380V/173V、50Hz、Y-Y连接，触发角为0°。整流回路为三相桥同相逆并联结构。负载为5欧纯电阻。整流系统控制器以株洲科瑞变流电气有限公司提供。诊断系统采用DSP(TMS320F2812）和单片机(89C52）的双CPU结构，DSP负责实时数据采集、处理和故障分析，MCU主要负责人机交互、远程通信等。实验原理图如图2。

采样频率:由于系统中信号频率主要集中在低频部分，采样频率设置为1KHz。通过滤波处理后即可以完整地再现采样信号中频率不超过500Hz的信号，小波包分解将信号0～500Hz频率范围内的信号分成了八段。

(2）基于db3的小波包特征值提取及数据库建立

第一步:将故障样本A、B、C三相电流信号利用“db3”小波进行三层小波包分解，得到第一到第八共23组高、低频段分段系数序列 dj，(j=1，2，...n）。

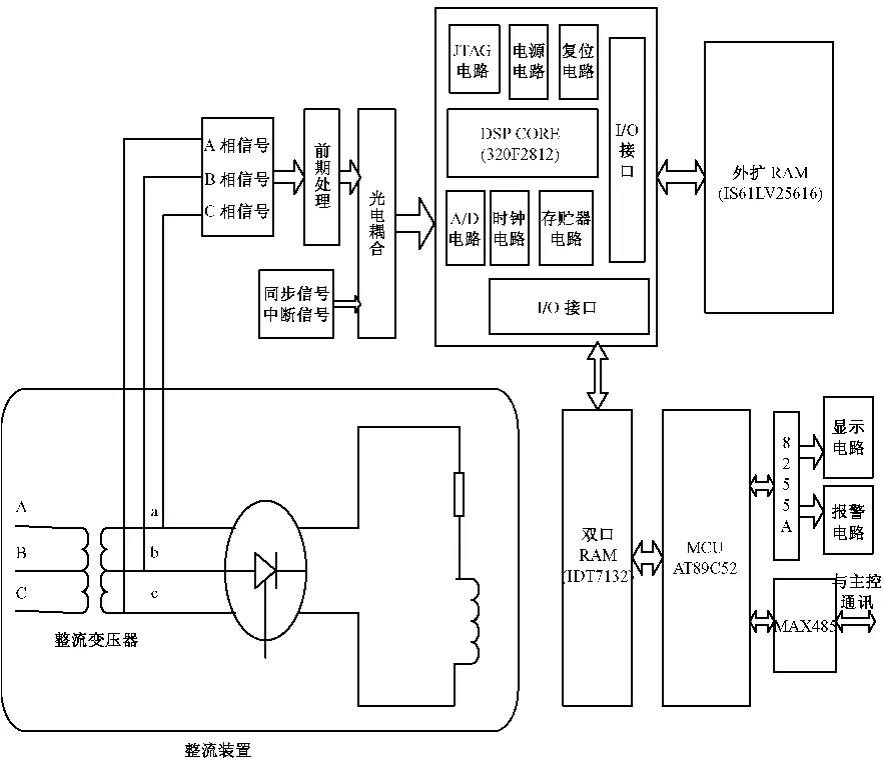
图2 实验原理图Fig.2 Configuration of experiment principle

第二步:求各段分解系数序列的能量。设Ei为第三层小波包分解第i组频段系数的能量，就有

第三步:特征向量的构成，按频段顺序，以各段小波包分解系数的能量为元素得到一组与信号对应的序列(E1，E2，…，En），求该序列的总能量 E=E1+E2+…+En，则可由此确定对应的特征向量为:

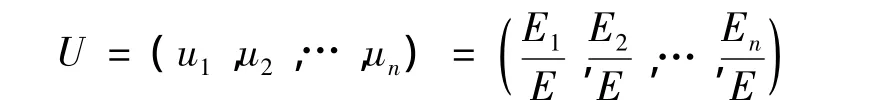
依上三步，可以得到各种状态下的特征向量。

实验中共形成了43种情况采集的数据形成了特征向量样本数据库。本文列出样本中具有代表性的三种情况的特征向量如表1所示。

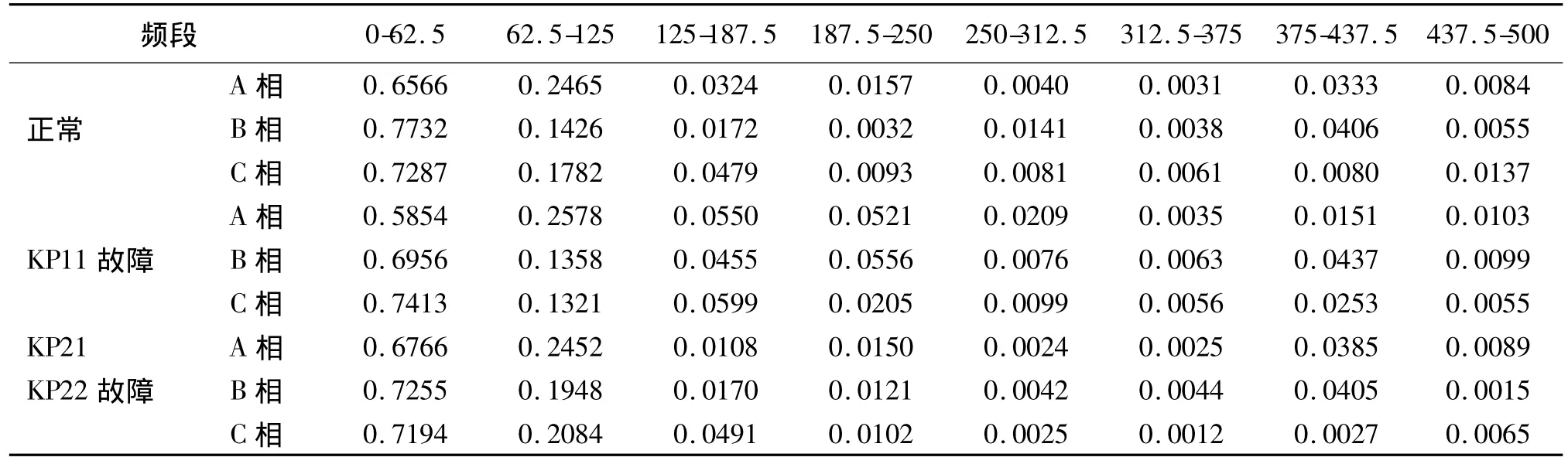
表1 多种状态下特征向量Tab.1 Eigenvector of different states

(3）模糊诊断过程

基本思路:系统运行时，不间断采集A、B、C三相电流信号形成待检向量，并与正常状态的向量进行比较，当故障状况发生时，则启动诊断过程。诊断时，将待测信号与样本数据库中数据利用模糊识别方法，确定待测信号的故障类型。

实验中假设kp11出现断开故障为待识别状态，变压器阀侧A、B、C三相的采集该识别状态信号波形图如图3所示。

利用特征值求法，求得的信号的特征值如表2所示。

运用公式(3），求出待测信号特征值向量与各种状态(文中列出了九种状态）时信号特征值向量的散度如表3所示。

表2 待测信号向量Tab.2 Eigenvector of signal

运用降半哥西公式(4）可求得待测信号特征向量与其他数据样本特征向量相似程度的隶属度如表4所示。

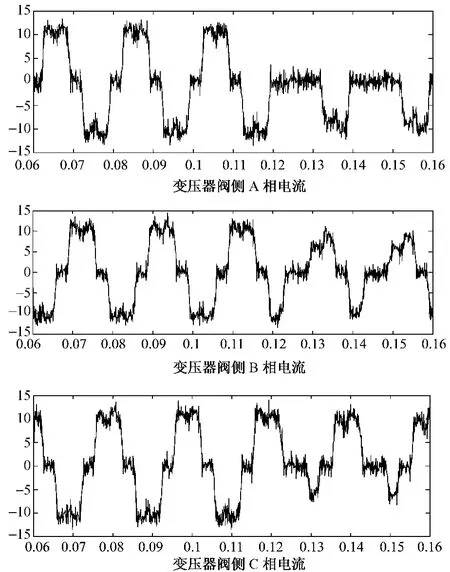
图3 实验波形Fig.3 Experimental waveforms

隶属度求出后，则利用最大隶属度模糊判断方法实现模糊诊断。首先，选出A、B、C三相对应的隶属度最高的那一项，如表5所示。

然后，选出隶属度较大的几种状态:从以上表5可看出，待测状态为 KP11故障、KP13故障、KP16故障、KP11与KP12同时故障的可能性比较大。它们分别是:

这时故障情况很难精确诊断，采取解决的方法是用连乘法:同一状态情况，隶属度连乘，精确诊断:U(kp*）=U1(A）*U2(B）*U3(C），可得出:

最后确定诊断:从系统最后计算的结果可以看出U(kp11）最大，即待测信号与KP11故障状态信号匹配隶属度最大，说明系统处于KP11故障状态。

由以上各步骤完成了系统的故障诊断过程。

表3 待测信号与各信号特征值散度Tab.3 Eigenvector divergence of signals

表4 待测信号与各信号特征值隶属度Tab.4 Eigenvector membership of signals

表5 待测信号与各信号隶属度最大值Tab.5 Maximum of signals membership

5 结论

针对同相逆并联大功率整流装置，基于整流变压器阀侧三相电流信号，进行模糊诊断系统的研究与设计。信号特征值通过对三相电流信号进行三层小波包分解后获得的能量谱而形成，对多种状态分析形成了样本特征向量数据库;利用模糊诊断中的J散度、降半哥西公式和最大隶属度原则对待识别状态与样本数据库中的特征向量进行处理，获得待检状态与某一样本状态的最佳匹配，实现了模糊识别。通过实验验证，在小电流实验环境，该系统能正确地诊断出系统故障，性能较好。

References）:

［1］黄俊，王兆安(Huang Jun，Wang Zhaoan）.电力电子变流技术 (Power electronic conversion tech.）［M］.北京:机械工业出版社 (Beijing:Machinery Industry Press），1999.

［2］周鹏，欧阳波(Zhou Peng，Ouyang Bo）.同相逆并联整流装置故障诊断系统的研究 (Study of fault diagnosis system on cophase counter parallel in rectifier unit）［J］.电力电子技术(Power Electronics Tech.），2009，43(1）:43-45.

［3］Frank P M.Fault diagnosis in dynamic systems using analytic and knowledge-based redundancy-A survey and some new results［J］.Automatic，1990，26(3）:459-474.

［4］刘颖，张明(Liu Ying，Zhang Ming）.基于模糊理论和频谱分析的电力电子设备的故障诊断(Fault diagnosis of power electronic circuits based on fuzzy theory and frequency spectrum analysis）［J］.海军工程大学学报 (J Naval Univ.of Eng.），2005，17(1）:85-88.

Study of fault diagnosis system in rectifier units based on wavelet packet and fuzzy diagnosis

KUANG Yong-hong1，OUYANG Bo2，ZHOU Peng2
(1.Applied Technical College of Hunan Institute of Engineering，Xiangtan 411101，China;2.School of Information Science and Engineering，Central South University，Changsha 410075，China）

According to the cophase counter parallel connection rectifier units widespreadly used in the fields of power and chemical industry，the paper presents a wavelet packet-fuzzy recognition method with the three phase current at rectifier transformer side as the diagnosis signal to realize fault diagnosis.Firstly，the fault eigenvalues are extracted with wavelet packet analysis to form a sample database，then the fuzzy recognition of sample status are identified by using J dispersion and maximum membership principle.The method is verified by experiments，and the accuracy is excellent.

cophase counter parallel connection;fault diagnosis;wavelet packet analysis;fuzzy reasoning

TM 461;TM935

A

1003-3076(2010）03-0030-05

2009-09-20

旷永红(1979-），女，湖南籍，讲师，主要从事变流器信号与信息处理方面研究;

欧阳波(1962-），男，广东籍，副教授，主要从事大功率变流控制技术研究。