基于注入电流不平衡量的配电网改进潮流算法
祝洪博,刘新伟,邵萌萌,贾建夫,杨龑亮
(1.东北电力大学,吉林省吉林市 132012;2.吉林省电力公司培训中心,吉林长春 130022)
基于注入电流不平衡量的配电网改进潮流算法
祝洪博1,刘新伟1,邵萌萌1,贾建夫2,杨龑亮1
(1.东北电力大学,吉林省吉林市 132012;2.吉林省电力公司培训中心,吉林长春 130022)
本文在节点注入电流模型配电网潮流计算的基础上,采用了基于注入电流的不平衡量,对算法进行了改进和简化,将Jacobian矩阵作为一个固定矩阵,从而使计算量大大减少,提高了计算速度;通过引入最优乘子,从算法上保证了潮流计算的不发散,有效地解决了潮流计算对初值的敏感性以及一些病态系统的潮流计算问题。用30节点、141节点配电网算例和几种典型的病态系统的计算验证了算法的有效性和可行性。
配电网;潮流计算;最优乘子;病态
引言
配电网潮流计算是配电网经济运行、系统分析等的重要基础[1]。目前,输电系统潮流计算方法已较为成熟而且获得了广泛的实际应用。但由于配电网与输电网有着明显的差异:配电网通常呈辐射状,支路比值较大,分支线较多;传统的牛顿法和快速分解法在应用于配电网潮流计算时容易形成病态而无法收敛,因此,研究适合于配电网的潮流算法是至关重要的。
许多学者结合配电网特殊的网络结构,研究开发出一些适合于低压配电网的母线类和支路类潮流算法,例如母线类的 Zbus[2]法和 Ybus[3]法,支路类的前推回推法、基于回路方程的算法、改进的牛顿-拉夫逊法等。基于节点注入电流模型的配电网潮流计算[4]是以节点注人电流为变量列出潮流方程,它同牛顿法相似,在每次迭代时都需要重新计算Jacobian矩阵,使计算速度大大降低,同时,配电网有时会因初值选取不当,无功紧张或其它原因导致电压质量很差,在进行潮流计算时会出现病态的问题。针对上述的问题,本文采用基于注入电流的不平衡量,对算法进行了改进和简化,将Jacobian矩阵作为一个固定矩阵,从而使计算量大大减少,提高了计算速度;通过引入最优乘子,有效地解决了配电网中病态潮流的计算问题。
1 节点注入电流模型的改进
对于单电源的配电网,取该电源点为平衡节点,其余节点为PQ节点;而对于多电源的配电网,选取其中的一个节点为平衡节点,另外的电源节点为PV节点,剩余的节点为PQ节点。这里节点电压和注入功率以及线路导纳都由直角坐标来表示。
(1)对PQ节点的处理
在文献[4]的基础上,引入了注入电流的不平衡量 ΔIi,设 ΔIi= Δai+jΔbi,将实部,虚部分开,则可得基于节点注入电流模型的非线性潮流方程。(式中Δai和Δbi为注入电流的不平衡量)。
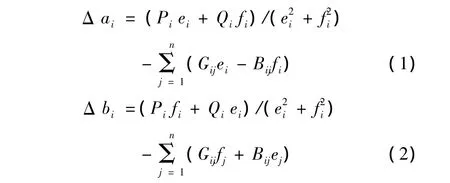
再对 Δai,Δbi的非线性方程(即式1,2)运用梯度法求解,则可得潮流的修正方程为:
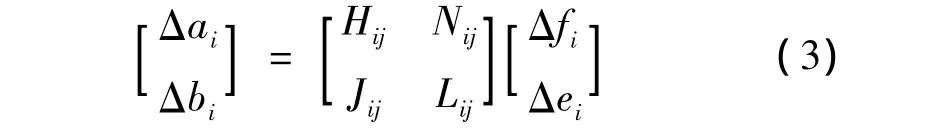
其中,Δei,Δfi为除平衡节点外的节点电压增量的列向量。
式(3)中Jacobian矩阵各元素为:
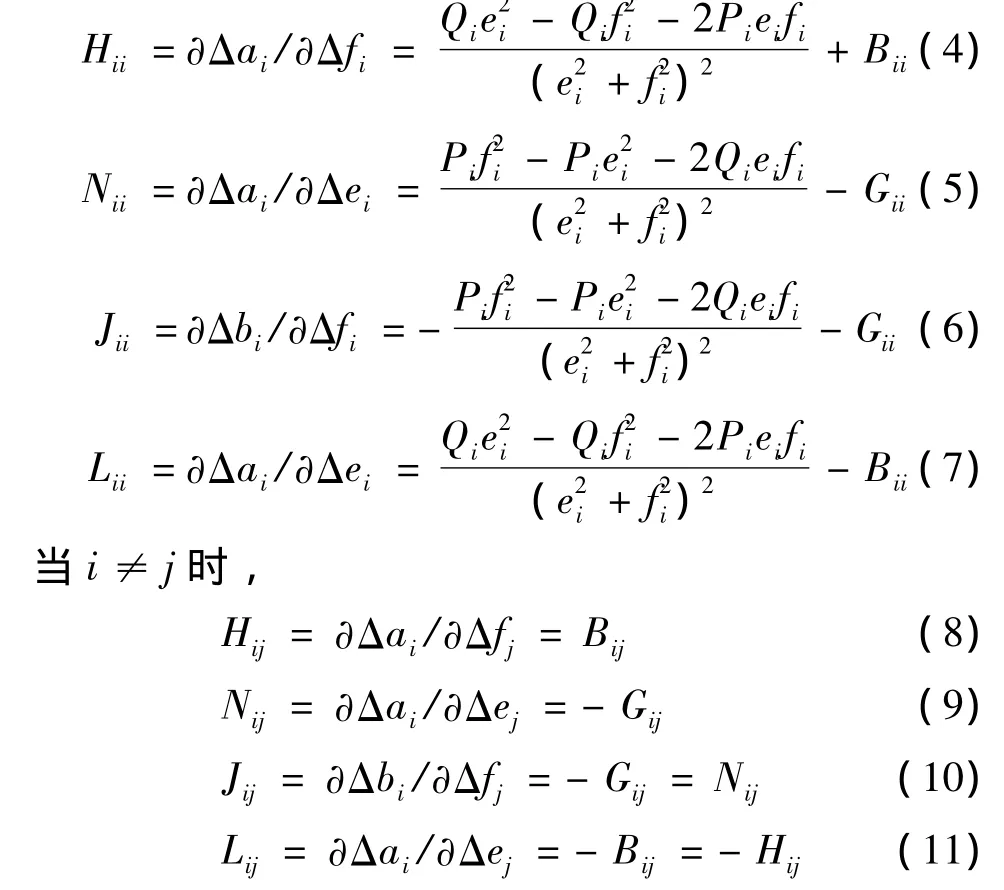
当i=j时量级为10-1~10-2,+的值的数量级为10-1~100。因此可以认为式(4)、(5)、(6)、(7)中等号右边后半部分的绝对值远大于前面部分的绝对值,因此,可以对以上四个式子进行简化:当i=j时,
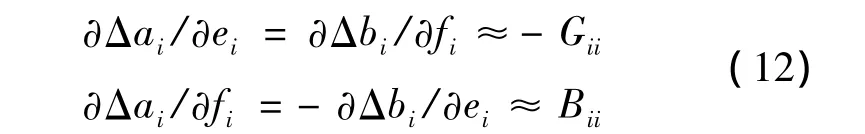
在实际配电网潮流计算中,式(4)、(5)、(6)、(7)中等号右边的两部分的数值是相差很大的,通过许多例子可以发现二者的差距为1-3个数量级。一般来说,系统的线路电阻和电抗标幺值的数量级为10-3~10-1,从而 Gii和 Bii的值的标幺值的数量级为101~103。而负荷节点的功率值Pi和Qi的数
(2)对PV节点的处理
对于多电源的配电网,选取其中的一个节点为平衡节点,另外的电源节点为PV节点。对PV节点来说,由于无功注入量未知,无法得到ΔIi,因此,这里仍采用常规的牛顿法进行处理。
2 病态潮流问题的解决
在实际配电网潮流计算中,经常会因初值设得不合理,无功紧张或其它原因导致电压质量很差、有重载线路而导致节点间相角差很大或其它原因,往往会出现计算过程的发散和振荡的现象[5-6]。因此,引入了最优乘子[7],就是在第k次迭代求得状态变量的修正量Δx(k)之后,不直接用Δx(k)去修正x(k),而是乘以一个标量乘子μ后再去修正,即用μ修正后的值作为k+1次迭代的初值。同时μ的选取要满足:使潮流的误差方程的平方和取最小值。这在某种程度上限制了对x(k)的修正,避免产生过修正或者欠修正,保证了潮流计算的不发散。因此,它能较好地处理配电网中病态潮流的计算问题。
采用功率型直角坐标的潮流方程的泰勒展开式可以精确地表示为
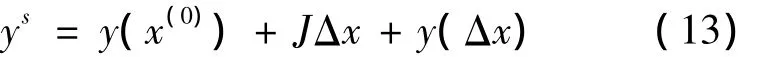
对于采用注入电流不平衡量的PQ节点[8]来说,此时上式中等号右端第三项中的各元素将为零,因此该项中仅对应于PV节点的元素有值,其余元素均为零。这样构造的目标函数为

通过对F(x)对μ求导,并令其等于零;
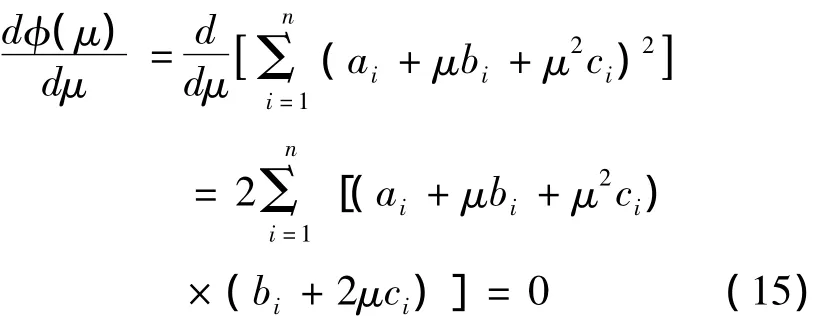
将上式展开,可得
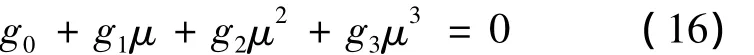
式(16)可用牛顿法或卡丹(Cardan)公式来求解,所得解μ值即为最优乘子μ*。
改进算法的计算流程如图1所示。
其中各变量的定义如下:
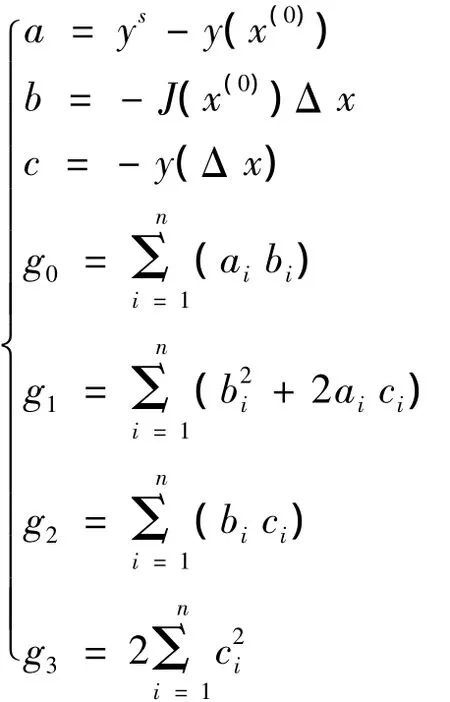
3 算例分析

图1 改进算法的流程图Fig.1 Flow chart of improved algorithm
利用本文方法和文献[4]算法分别对单电源的30节点配电网算例进行了潮流计算,计算结果比较如表1,原始数据参考文献[9]。对多电源的配电网来说,选取双电源的141节点配电网进行了潮流计算,计算结果比较如表2,原始数据参考文献[4]。本文对30节点的初值选取收敛性也进行了比较如表3。这里的算法程序通过VB6.0来实现。还对一般方法难以收敛的病态系统(如13节点系统和43节点系统)进行了潮流计算,计算结果如表4。

表1 单电源30节点配电网的计算结果Tab.1 30-node 1-source distribution system
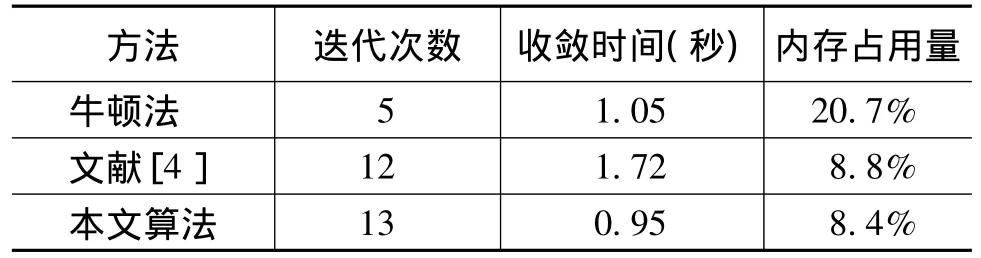
表2 双电源141节点配电网的计算结果Tab.2 141-node 2-source distribution system
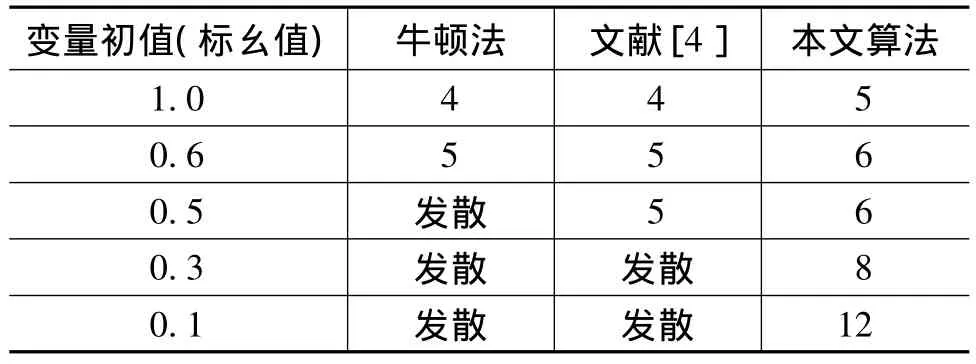
表3 对30节点初值选取的收敛性比较Tab.3 Convergence comparison for 30-node selected initial

表4 对处理病态系统的计算结果Tab.4 Calculation results for ill-conditioned system processing
由表1可以看出,对单电源的30节点系统来说,本文算法同牛顿-拉夫逊法相比,大大节省了内存,而同文献[4]相比,也节省了内存,虽然收敛次数增加,但每次收敛的时间却大大减少,从而总的收敛时间也减少了。
由表2的计算结果表明:对双电源的141节点的系统来说,由于存在PV节点,对它的处理采用常规的牛顿法处理,每次迭代时只需更新与PV节点有关的Jacobian矩阵元素即可,再加上在实际配电网中PV节点较少,因此,虽然收敛次数增加,但它总的收敛时间比牛顿法和文献[4]都要短,而且也节省了内存。
由表3表明:当牛顿-拉夫逊法的节点电压初值低于0.5时,潮流开始发散(或振荡);而文献[4]算法的节点电压初值低于0.3时,潮流也开始发散(或振荡);本文的算法由于引入了最优乘子[10],算法稳定性比牛顿法和文献[4]算法都好,当节点电压初值低于0.1时,仍能可靠地收敛。
由表4可以看出:对一些病态系统(如13和43节点系统),牛顿法和文献[4]算法均难以收敛,而本文的算法却能保证潮流可靠地收敛。
4 结论
本文充分利用了配电网不同于输电网的特点,在基于电流模型的配电网潮流计算的基础上进行了简化和改进,不仅提高了计算速度,也节省了内存,而且通过引入最优乘子,保证了潮流计算的不发散,有效地解决了病态潮流的计算问题,可有效地运用于复杂单电源和多电源配电网的潮流计算。同牛顿-拉夫逊法和文献[4]算法相比,节省了内存,虽然收敛次数增加,但每次收敛的时间却大大减少,从而总的收敛时间也减少了,从而提高了计算速度;并且解决了潮流计算对初值的敏感性以及一些病态系统的潮流计算问题,通过算例证明了该算法的有效性和可行性。
References):
[1]张学松,柳焯(Zhang Xuesong,Liu Zhuo).配电网潮流算法比较研究 (Comparative study on power flow algorithm of distribution network)[J].电网技术 (Power System Tech.),1998,22(4):96-100.
[2]Chen T S,Chen M S.Distribution system power flow analysis a rigid approach[J].IEEE Trans.PWD,1991,6(3):1146-1152.
[3]Tripathy S C,Prasad G D,Malik O P.Load-flow solutions for ill-conditioned power system by a Newton-like method[J].IEEE Trans.on PAS,1982,101(10):3648-3657.
[4]鄢长春,张焰,陈章潮 (Yan Changchun,Zhang Yan,Chen Zhangchao).基于节点注入电流模型的配电网潮流算法(Distribution system power flow calculation based on the node current-injection model)[J].电力系统自动化 (Automation of Elec.Power System),1999,23(7):55-58.
[5]诸骏伟(Zhu Junwei).电力系统分析(Power system analysis)[M].北京:中国电力出版社 (Beijing:China Elec.Power Press),1995.
[6]刘广一,胡锡龙,于尔铿 (Liu Guangyi,Hu Xilong,Yu Erkeng).电力系统病态潮流计算新算法(A new calculation algorithm of power system ill condition power flow)[J].中国电机工程学报 (Proc.CSEE),1991,11(S1):27-36.
[7]Iwamoto S,Tamura Y.A fast load flow method retaining nonlinearity[J].IEEE Trans.on PAS,1978,100(4):1736-1737.
[8]王承民,蒋传文,侯志俭(Wang Chengmin,Jiang Chuanwen,Hou Zhijian).基于节点不平衡功率的病态潮流算法(Ill-conditioned load flow algorithm based on node lopsided powers)[J].上海交通大学学报 (J Shanghai Jiaotong Univ.),2004,38(8):24-28.
[9]K Cespedes.New method for analysis of distribution networks[J].IEEE Trans.on Power Delivery,1990,1(22):1736-1737.
[10]石飞,赵晋全,王毅 (Shi Fei,Zhao Jinquan,Wang Yi).计及发电机无功约束的最优乘子潮流计算方法的比较(A comparison of Newton-raphson optimal multipliers load flow methods condisidering generator reactive power limitation)[J].电力系统保护与控制 (Power System Protection& Control),2008,37(2):54-59.
[11]卢明富,梅生伟(Lu Mingfu,Mei Shengwei).小世界电网生长演化模型及其潮流特性分析 (Evolutive model of small-world power grid and its power flow analysis)[J].电工电能新技术 (Adv.Tech.of Elec.Eng.&Energy),2010,29(1):25-29.
Improved power flow calculation of distribution network based on injection current imbalance
ZHU Hong-bo1,LIU Xin-wei1,SHAO Meng-meng1,JIA Jian-fu2,YANG Yan-liang1
(1.Northeast Dian Li University,Jilin 132012,China;2.Training Center in Jilin Province Power Company,Changchun 130022,China)
Based on the power flow calculation of distribution network of the node current-injection model,the injection current imbalance is adopted to improve and simplify the algorithm,to make Jacobian matrix a fixed matrix,and computation is greatly reduced and the computing speed is improved.An optimal factor is introduced to ensure the convergence of the computing process,and the sensitivity of the initial value about power flow calculation and some ill-conditioned systems problems are also resolved effectively.Using the distribution network of 30-node,141-node and several typical examples of ill-conditioned systems verify the effectiveness and feasibility of the method.
distribution network;power flow calculation;optimal factor;ill-conditioned
TM744
A
1003-3076(2010)03-0022-04
2009-08-24
祝洪博(1942-),男,吉林籍,教授,研究方向为配电自动化、人工智能等;
刘新伟(1983-),男,山东籍,硕士研究生,主要研究方向为配电自动化。

