菱形车转向机构的分析与优化

查云飞 钟志华 闫晓磊

湖南大学汽车车身先进设计制造国家重点实验室,长沙,410082

0 引言

转向系统是用来保持或者改变车辆行驶方向的机构,在车辆转向行驶时,保证各转向轮之间有协调的转角关系。传统的四轮车辆通过转向传动结构来调节左右两个前轮同时偏转以实现转向。这种传统的车辆由于前、后、左、右各车轮平行设置,因此,其转弯半径相对较大,操作也不是很灵活。菱形车四个车轮按前后各一个、中间两个呈菱形布置,其转弯半径较小,操作灵活。传统车辆的四轮转向效果与菱形车的四轮转向机构相比,在相同轴距和转角情况下,菱形车的转向半径明显小于一般轿车的转向半径[1-2]。

自钟志华院士提出菱形车概念以来,很多学者对菱形车进行了分析研究[3-5]。本文拟运用有限转动张量和空间解析几何的方法建立菱形车转向拉杆机构参数化运动模型,通过遗传算法对转向拉杆的参数进行优化,为菱形车的工程化提供理论支持。

1 转向系统机构优化设计问题的提出

传统车辆车轮转向示意图如图1所示;菱形车辆车轮转向示意图如图2所示。菱形车特殊的底盘结构导致了一般轿车的转向系统无法在其上布置,因此菱形车的转向系统采用了前后联动转向机构。前后联动转向机构与传统的转向机构一样,包括转向操纵机构、转向器和转向传动机构三大部分,如图3所示。其中转向操纵机构与普通轿车的并没有区别,针对菱形车特殊的结构设计了两级齿轮的转向器,转向传动机构则由三大机构组成,分别为前轮转向拉杆机构、过渡拉杆机构和后轮转向拉杆机构。其中过渡拉杆机构为一对称结构,通过中间反向摆臂使前后轮转向相反,前轮转向拉杆机构与后轮转向拉杆机构则为四连杆机构,以实现前后轮联动转向。根据转向拉杆机构的相似性,在此仅取前轮转向拉杆机构进行分析,后轮转向拉杆机构可以类推。

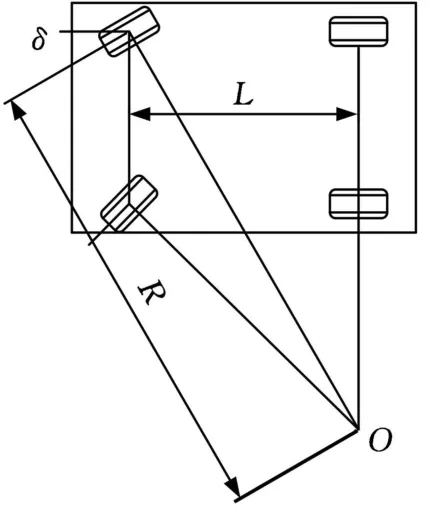
图1 普通布置车轮转向示意图

图2 菱形布置车轮转向示意图

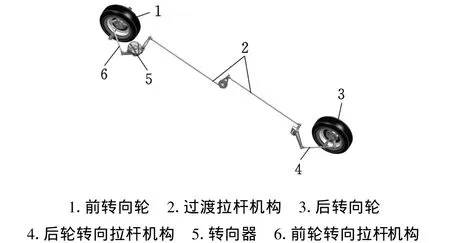
图3 菱形车转向系统模型

如图4所示,转向拉杆机构的转向节连杆与悬架的摆臂在车辆的中心面投影设置成等长且平行,连杆随着车轮做与摆臂相同的运动以减小被动转向,且转向节连杆位于与主销垂直的平面内。

图4 拉杆机构与悬架模型

根据文献[6]要求,当汽车前行向左或向右转弯时,转向盘向左向右的回转角和转向力不得有显著差异,转向系统必须保证驾驶员在正常驾驶操作位置上能方便、准确地操作。当车轮跳动了一定的高度后,车轮的转角会与未跳动时有一定的变化,这将影响到转向系统的准确性。四连杆机构在受空间结构限制的情况下输入角转动相同的角度时,向左和向右的回转角不一定能相等。因此,要通过拉杆机构的长度和位置参数使得车轮的跳动对转角的影响尽可能降到最低,同时使得车轮向左转向右转的角度差尽可能小。

2 转向器输出摆臂与转向节摆臂的转角关系

2.1 坐标系的确定

为分析前轮转向拉杆机构的运动,整体坐标系Y方向取为整车运动方向的左侧,Z方向取为方向机输出臂运动平面的法线方向,X方向则由右手法则确定,坐标原点O与转向器输出臂的I点重合。根据以上坐标系建立了如图5所示的菱形车前轮转向拉杆机构空间拓扑结构,图中,IE为转向器输出摆臂,绕支撑轴CD转动,IE垂直CD于点I;HF为转向节摆臂,绕转向轮主销AB转动,HF垂直AB于点H。E、F点分别为摆臂铰点,EF为转向节连杆。

图5 菱形车转向拉杆空间拓扑结构简图

2.2 各点坐标的确定

这里取IE长为l1,与Y方向的夹角为θ1,HF长为l2,与Y方向的夹角为θ2,EF与Y方向的夹角为θ3。由于转向节连杆EF与悬架的摆臂在车辆的中心面投影等长且平行,而悬架的摆臂由整车的结构确定,取为x,则转向节连杆EF的长度l3为

要确定转向器输出摆臂与转向节摆臂的转角关系,需要确定图5中各关键点的坐标。

2.2.1 跳动角度的确定

车轮跳动一定高度ΔH时,会引起转向节连杆在XZ平面上的投影绕E点转动λ角,如图6所示。在这里不考虑悬架橡胶衬套的变形,由几何关系可得到λ角与ΔH的关系：

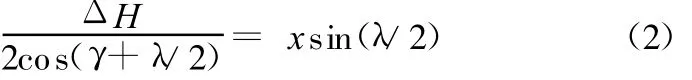
式中,γ为主销的后倾角。

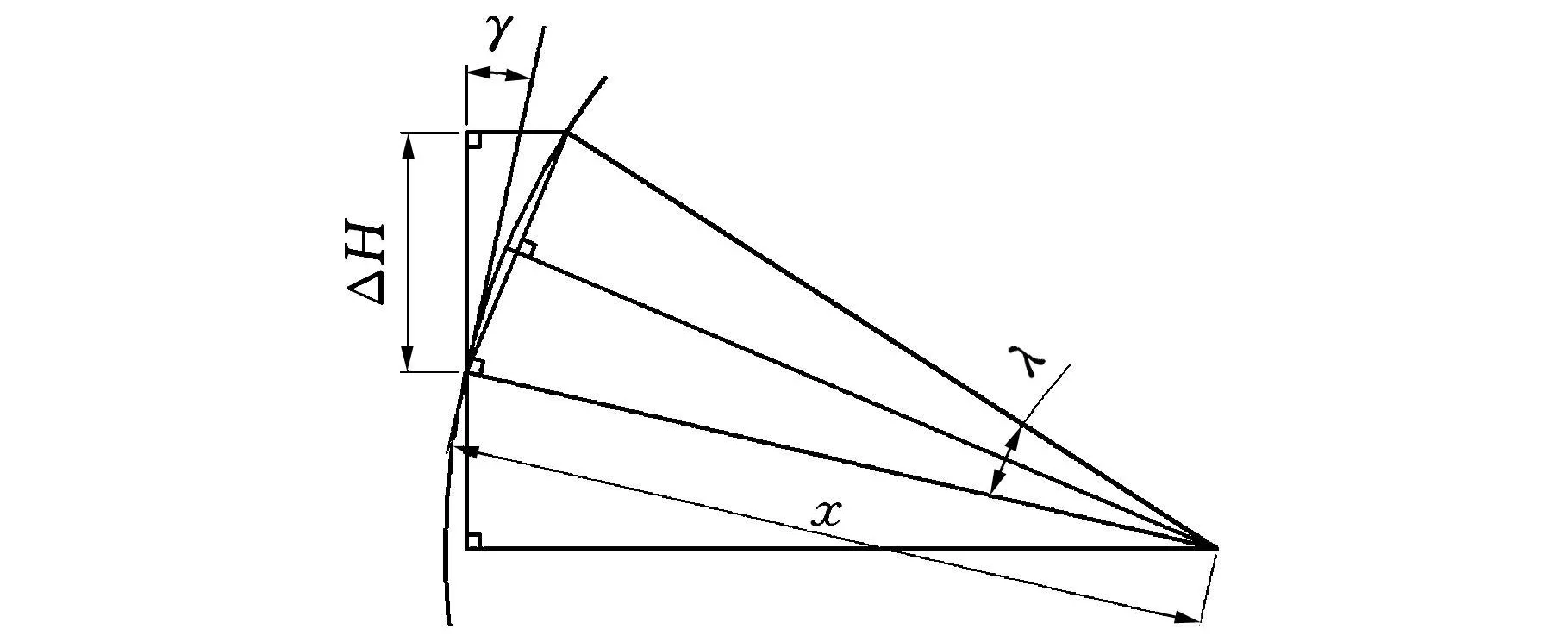
图6 λ角与ΔH的关系图

2.2.2 H、H′点坐标计算

根据图5所示转向拉杆结构,I点的整体坐标为(0,0,0),根据几何关系可以计算出 H点的整体坐标：

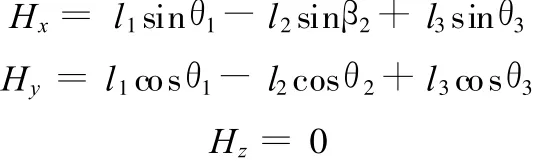
同理,车轮跳动后的H′点坐标为

2.2.3 E点坐标计算

E点在转向拉杆机构的运动过程中始终处于O1 X 1Y 1平面内,并且在以I点为圆心、IE为半径的圆上摆动,因此,E点坐标为

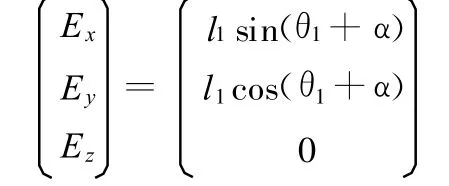
当转向器输出摆臂处于初始位置时,E点的坐标为

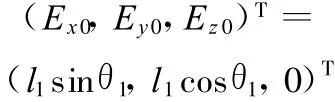
2.2.4 F、F′点坐标计算

同理,F、F′点在转向拉杆机构运动的过程中始终处于O2 X 2Y 2和O3 X 3Y 3平面内,并且分别在以 H、H′点为圆心,HF、H′F′为半径的圆上摆动,因此F 、F′点坐标为：

当转向节摆臂处于初始位置时,F、F′点的坐标为：

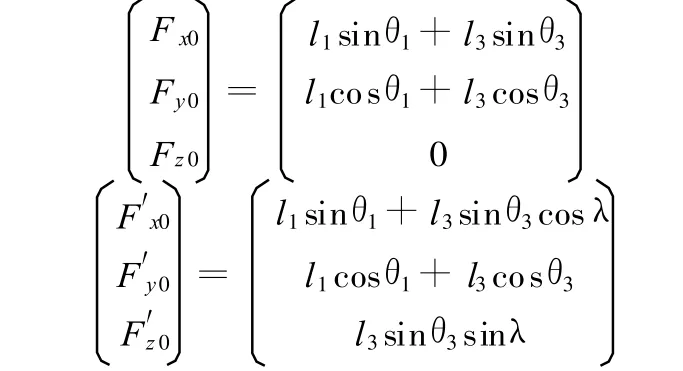
2.3 转角关系方程的建立

当设计前转向轮向某一方向转动β1角度时,即转向节摆臂HF绕车轮主销AB任意摆动β1角时,转向器输出摆臂IE绕支撑轴CD摆动α角。当转向器输出摆臂IE绕支撑轴CD摆动相同的α角时,跳动情况下转向节摆臂H′F′绕跳动后的主销A′B′摆动β2角。当转向器输出摆臂 IE绕支撑轴CD摆动-α角时,转向节摆臂HF绕车轮主销AB摆动β3角。定义单位矢量o、p、q分别沿转轴CD 、AB 和A′B′。当转向节摆臂 HF 转动 β1角到HF 1时,方向机输出摆臂IE 、转向节摆臂H′F′分别转动 α、β2角到 IE1、H′F′1,应用有限转动张量 ,有：

式中,I为单位并矢;P为矢量;p为对应的张量。

同理：

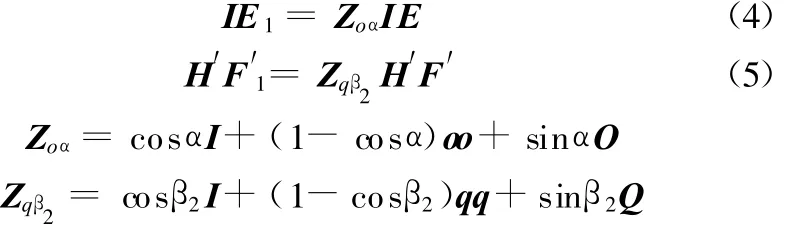
式中,O为矢量o对应的张量;Q为矢量q对应的张量。

由式(3)、式(4)可得到未跳动时两摆臂转角关系的超越方程[7]：

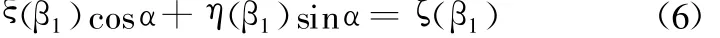
由式(6)可得

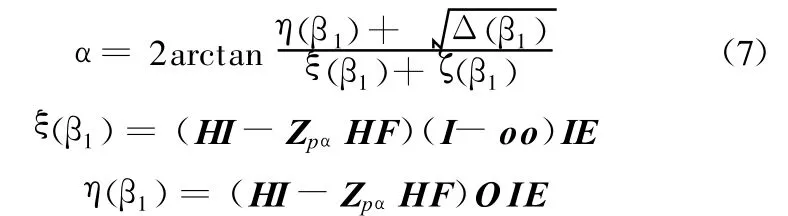
由式(4)、式(5)可得到跳动后两摆臂转角关系的超越方程：

由式(8)可得

当转向器输出摆臂IE转动-α角时,根据式(3)、式(4)可得到两摆臂转角关系的超越方程：

由式(10)可得

3 结构的遗传算法优化

3.1 优化目标的建立

车轮跳动一定高度 ΔH时,转向节摆臂由HF跳到H′F′位置。当转向器输出臂IE绕I点转动α角到IE 1时,转向节摆臂 HF、H′F′分别绕H 、H′点转动β1和β2角到 HF1、H′F′1位置 。由于车轮跳动导致的变化为

当转向器输出摆臂向相反方向转动-α角时,转向节摆臂摆动β3,向左和向右的转角差可表示为

将式(9)、式(11)分别代入式(12)、式(13),就可得出车轮跳动所造成的转角变化关系和车轮向左转向右转的转角差。

近年来得到快速发展的遗传算法,是一类模拟达尔文自然进化论的仿生随机优化方法。通过在一组当前潜在解之间进行一定的遗传操作,如选择、杂交和变异,产生更好的解。这一过程反复进行,直至找到一个可以被接受的解。遗传算法较之其他搜索技术具有许多优越性,具体体现在鲁棒性、固有并行性和全局性。

优化设计的目的是使实际值尽量接近理想值,根据转向拉杆机构具体结构确定优化变量、优化目标以及搜索域。选取转向器输出摆臂IE长度为l1,与Y方向的夹角为θ1,转向节摆臂HF长度为l2,与Y方向的夹角为θ2,转向节连杆EF与Y方向的夹角θ3为设计变量。取车轮跳动后导致的车轮最大转角的变化maxΔβ1,车轮向左转向右转所产生的最大角度差maxΔβ2为优化目标。菱形车转向拉杆机构的运动学目标函数表达式如下[8-10]：

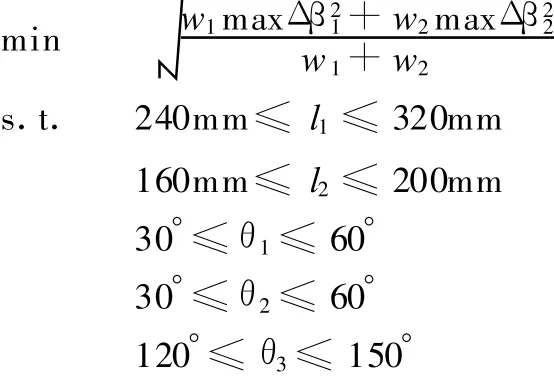
式中,w1、w2为加权系数。

转向系统必须保证将驾驶员的操作准确地传递到转向轮,过大的车轮跳动带来的角度差Δβ1和过大的转向轮向左转和向右转角度差Δβ2都是不允许的,根据样车检测,Δβ1和 Δβ2在同一个数量级上,因此在此 w1、w2都取为0.5。转向拉杆机构的尺寸受到整个结构的约束,因此,优化变量的范围必须根据菱形车转向拉杆机构位置的许可空间确定,其余参数根据菱形车总体布置结构来确定。

3.2 数学模型的验证

在进行遗传算法优化之前,为了验证运动学方程的合理性,任意选取两组转向拉杆机构的参数,在ADAMS软件中建立虚拟样机模型。采用同样的转向拉杆机构参数,利用本文的公式推导出Δβ1和 Δβ2,两者结果对比如图7所示。图7a为选择车轮跳动100mm时,车轮从-45°到45°范围内角度差,图7b为选择车轮转动45°时,转向器向反方向转动相同的角度所产生的角度差。

从图7可以看出,两者结果非常一致,从而验证了本文转向拉杆机构运动学模型的正确性。由图7a中可以看出,车轮跳动前后角度的变化曲线为一凹形曲线,最大的角度差出现在许可范围的两端;由图7b中可以看出,车轮向左转向右转角度差曲线为一递增曲线,最大的角度差出现在转角最大的时候。因此,车轮跳动导致的车轮最大转角的变化maxΔβ1,车轮向左转向右转所产生的最大角度差maxΔβ2都出现在转角最大时。

3.3 优化结果及其分析

根据菱形车转向拉杆机构的运动学模型,计算车轮在100mm的垂向跳动过程中,由于车轮跳动所带来的在许可范围内的最大转向角度变化,以及当车轮向某一方向转动最大角度时向左转和向右转的角度差。图8所示为优化过程中的遗传算法寻优性能跟踪图,由图8可以看出,在变异到900代以后目标函数值得到了明显的收敛。

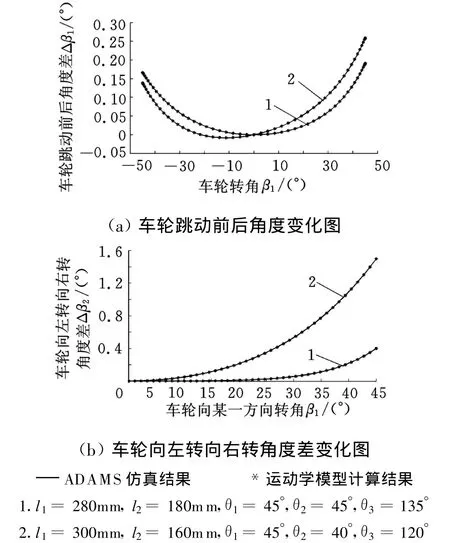
图7 ADAMS仿真结果与转向拉杆机构运动学模型计算结果对比

图8 遗传算法寻优性能跟踪图

表1所示为菱形车转向拉杆机构的部分优化解,设计人员可以根据拉杆机构的具体设计要求,选择满足设计要求的转向拉杆机构参数。从表1中可以看出,优化后的菱形车车轮跳动100mm时,最大转向角的变化可以控制在0.11°以内,向某一方向转动最大角度时,向左转向右转的角度差控制在0.032°以内,很好地优化了目标值。

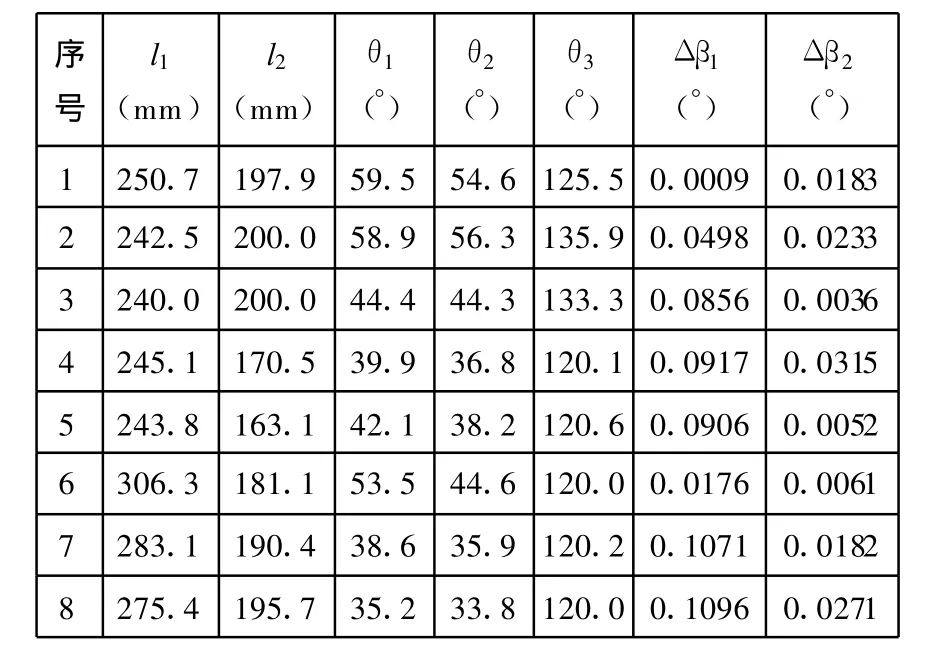
表1 菱形车转向导杆机构部分优化解

4 结束语

本文运用有限转动张量和空间解析几何法建立了菱形车转向拉杆机构参数化运动学模型,并验证了模型的正确性。基于该运动学模型,结合遗传算法,以摆臂、连杆长度和初始位置作为优化变量,对车轮跳动导致的转角变化和车轮向左转向右转的角度差进行了优化。通过对转向拉杆的参数优化,使得在设计转向系统时可以根据优化结果选择合适的摆臂、连杆参数。为菱形车的工程化提供了理论依据,具有实际工程应用意义。

[1] 余志生.汽车理论[M].北京：机械工业出版社,1999.

[2] 郑军.新概念车舒适性与操纵稳定性研究[D].长沙：湖南大学,2001.

[3] 毛建中,唐友名,钟志华.类菱形概念车中悬架优化设计[J].汽车工程,2007,29(2)：153-156.

[4] 黄智,钟志华.菱形新概念车转向性能分析[J].湖南大学学报(自然科学版),2006,33(6)：46-50.

[5] 查云飞,毛建中,钟志华.类菱形概念车转向传动机构设计与分析[J].交通标准化,2008(6)：193-196.

[6] 国家机械工业局.GB 17675-1999.汽车转向系基本要求[S].北京：中国标准出版社,1999.

[7] 洪嘉振.计算多体系统动力学[M].北京：高等教育出版社,1999.

[8] 袁传义,陈龙,江浩斌.电动助力转向系统多目标优化控制研究[J].中国机械工程,2007,18(14)：1757-1760.

[9] Mark E,Alex M,Jeffrey H.Multi-objective Optimal Design of Groundwater Remediation Systems：Application of the Niched Pareto Genetic Algorithm(NPGA)[J].Advances in Water Remurces,2002,25(1)：51-65.

[10] Vladimir G T,Hiroshi S,Georgy I T.A Method to Improve Multiobjective Genetic Algorithm Optimization of a Self-fuel-providing LMFBR by Niche Induction Among Nondominated Solutions[J].Annals of Nuclear Energy,2000,27(5)：397-410.