多特征信息融合的贝叶斯网络故障诊断方法研究

姜万录 刘思远

燕山大学,秦皇岛,066004

0 引言

液压泵是液压系统的心脏,对其进行有效的故障诊断是保证液压系统正常运行的关键。由于受流体的压缩性、泵与伺服系统的液固耦合作用、液压泵本身具有的固有机械振动和强噪声背景干扰的影响,使液压泵故障特征信息呈现出模糊性。当采用振动信号进行故障分析时,仅从单一域获取振动信号的故障特征信息存在不完备性。这两方面因素的影响给液压泵的状态监测与故障诊断带来了极大的困难[1-3]。

贝叶斯网络方法是目前不确定知识表达和推理领域最有效的理论模型,是解决模糊性问题的有效方法之一。贝叶斯网络的并行推理方式还能够提高诊断速度[4]。而多源信息融合技术能充分利用多个传感器信息,通过对各种特征信息的合理支配与使用,依据某种优化准则在空间和时间上把互补与冗余信息结合起来,产生对监测环境的一致性解释或描述,同时产生新的融合结果。利用这种技术可以大幅度地提高故障特征信息的完备性。

多源信息融合又称多传感器信息融合,所说的传感器是广义的,不仅包括物理意义上的各种传感器系统,也包括与观测环境匹配的各种信息获取系统[5]。本文将提取的振动信号多个故障特征当作来自多个不同传感器的多源信息,把每个故障特征都看成来自一个传感器。这样就可以利用多源信息融合技术进行多特征信息融合[6]。本文提出了将多源信息融合技术与贝叶斯网络相结合的故障诊断方法,使二者优势互补,可以在系统提供的信息具有模糊性和不完备性的前提下,发现故障并识别故障发生的类型。

1 液压泵故障机理

本研究的被诊对象是MCY14-1B型7柱塞轴向柱塞泵。在轴向柱塞泵的诸多失效形式中,松靴和脱靴是它最常见的故障形式。柱塞泵连续运转时,柱塞频繁吸油和排油,在这种交变载荷下长期工作容易造成柱塞球头和滑靴球窝的沉凹变形,这是引起松靴故障的主要原因。柱塞泵松靴故障严重时,柱塞将可能从滑靴中脱落造成脱靴故障,使液压泵失效。

1.1 松靴故障机理

当柱塞泵发生松靴故障时,缸体每旋转一周,柱塞球头与滑靴球窝在吸油区发生一次碰撞;当缸体转至排油区时高压油作用在柱塞上,使柱塞迅速向球头方向运动,与球窝发生第二次碰撞。缸体每旋转一周,柱塞球头与球窝发生两次碰撞,其振动经过传动轴和轴承传递到壳体上,所以单个柱塞松靴故障的振动频率为转轴频率的两倍,即[7]

式中,n为泵的转轴频率。

1.2 脱靴故障机理

当某一柱塞发生脱靴时,缸体在旋转过程中,该柱塞在吸油区将处于浮动状态,而在压油区回程盘驱动滑靴对该柱塞球头有一次撞击,所以脱靴故障的振动频率等于转轴频率,即[8]

2 贝叶斯网络

2.1 贝叶斯网络构建方法

贝叶斯网络采用有向无环图来表示随机变量的因果关系,通过条件概率将这种关系数量化。贝叶斯网络可以用一个二元组B=(G,θ)表示,其中,G是有向无环图,是对特征间依赖关系的定性说明,由一系列节点和从父节点指向子节点的有向边构成。节点对应于问题中的特征,有向边表示特征属性间依赖关系,没有有向边连接表示特征间条件独立。θ是描述网络布局条件概率的参数集合,定量地表示了各特征与其父节点的依赖关系[9]。

假定一个有限离散随机变量集合X={X1,X2,…,Xn},其中 ,X 1、X 2、…、Xn 对应于网络的各节点。

贝叶斯网络构建步骤如下：

(1)确定各故障模式及特征属性与网络节点的对应关系。

(2)建立表征条件独立的有向无环图。依据概率乘法公式有

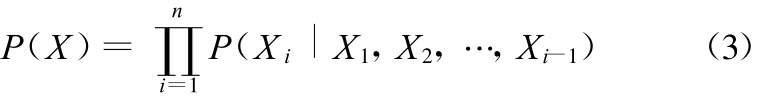
贝叶斯网络所描述的X上的联合概率分布可以由下式唯一确定：

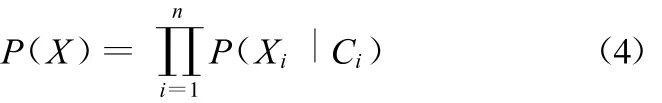
式中,Ci为Xi父节点的集合。

(3)确定节点概率分布参数。

2.2 贝叶斯网络构建过程

给定特征集合U={X1,X2,X3,X4,X5,Y},Y为故障类型集。依据贝叶斯网络的构建步骤建立特征间的贝叶斯网络。各节点的条件概率如图1所示。构建贝叶斯网络的同时也相应地得到了网络中每个节点的条件概率。

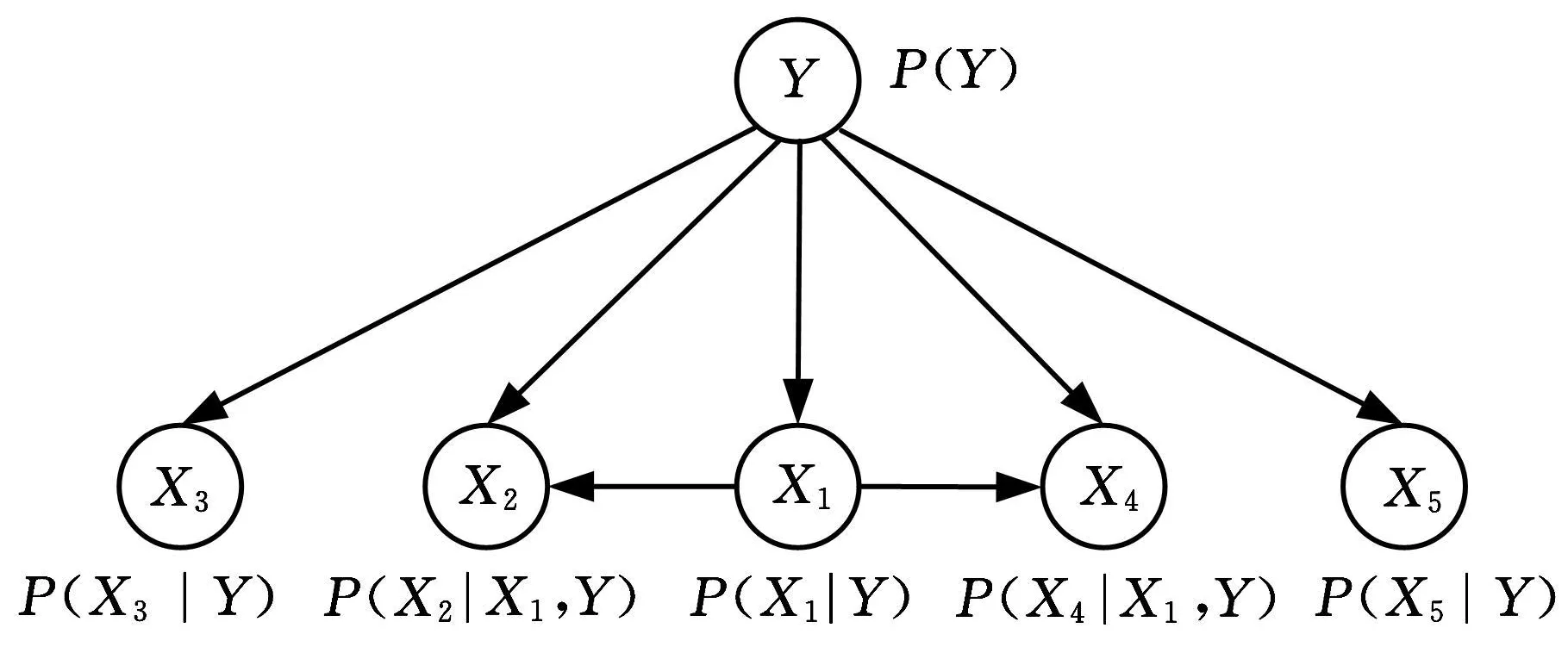
图1 贝叶斯网络示例

3 贝叶斯参数估计算法的多特征信息融合

根据液压泵故障信息的特点和试验条件,搭建了基于NI数据采集系统的振动信号检测及故障诊断试验平台。检测系统的多传感器观测数据是在强噪声背景中的同一特征的测量值。为增加故障特征信息的完备性,提高液压泵多模式故障诊断的正确率,利用振动传感器通过虚拟仪器采集故障振动信号,从频域和幅域两方面提取振动信号的多个故障特征,采用贝叶斯参数估计算法进行多特征信息融合。

设某一时刻被测样本有m个状态信息Yk={Y 1,Y 2,…,Y m},传感器的n个特征信息为X={X 1,X2,…,Xn},则此特征信息的测量模型是[10]

式中,f(Yk)为X与Yk的函数关系;υ为随机噪声。

信息融合算法是振动传感器n个特征信息的特征值,用按照某种估计准则函数M(X)估计出的状态Yk的真实值来表示。单个特征的估计计算过程如下：设其特征信息为Xi,状态Yk的估计值为Yˆk(Xi),并定义 L(Yˆk(Xi),Yk)为损失函数。根据贝叶斯估计,相应的损失函数的期望值,即风险表达式为

式中,P(Xi)为检测数据的分布概率;P(Yk|Xi)为状态Yk的后验概率。

取风险最小的估计准则,必须使

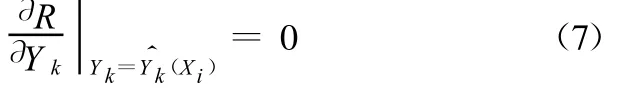
依据式(7)建立的准则,单个特征信息的最大后验概率最优估计值为

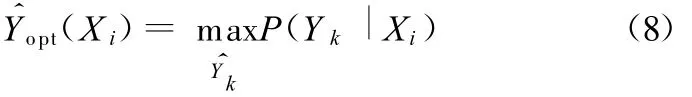
在系统中加入n-1个独立的特征信息后,最大后验概率估计值的算法与单个特征信息时是一致的。因此,n个特征信息的融合值为

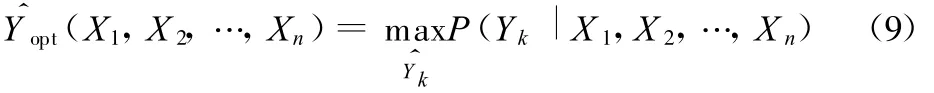
至此,多特征信息融合问题就转化为如何得到状态Yk的后验概率P(Yk|X)的问题,并找到相应的最大后验估计值。

4 贝叶斯分类器设计

4.1 两种故障模式的贝叶斯分类器

设Y l={Y 1,Y 2},X={X 1,X2,…,X n},其中Yl表示故障模式类别,X表示特征信息空间[11]。

定义判别函数为

将分类规则表示为 g(y)＞0属于Y 1类;g(y)＜0属于Y 2类;g(y)=0表示的是分类决策面方程,X为n维空间时,决策面为n维超平面,满足此方程则为故障误判。

构建各特征属性间相互条件独立的贝叶斯网络,并通过朴素贝叶斯(naive Bayesian,NB)分类方法简化式(11),得

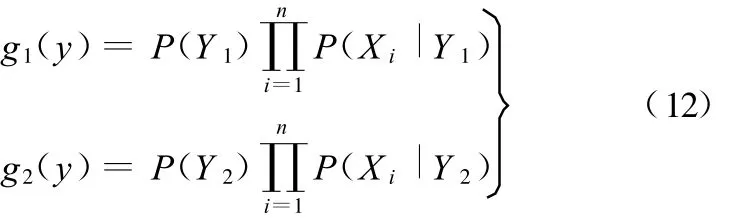
两种故障模式的分类器可以看作只是计算判别函数g(y)的一个“机器”,它根据计算结果符号对X分类。

4.2 多种故障模式的贝叶斯分类器

对提取的故障特征进行信息融合后,根据贝叶斯定理X={X 1,X 2,…,Xn},属于类Yj的概率为

2.4 两组患者术后满意度对比 观察组术后满意度显著高于对照组，差异有统计学意义(χ2=15.78，P<0.05)。见表5。

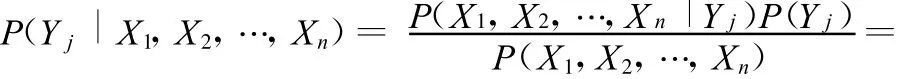
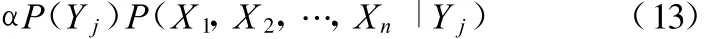
式中,α为正则化因子,α=1/P(X1,X2,…,Xn);P(Yj)为类Yj的先验概率。

式(13)还可以表示为

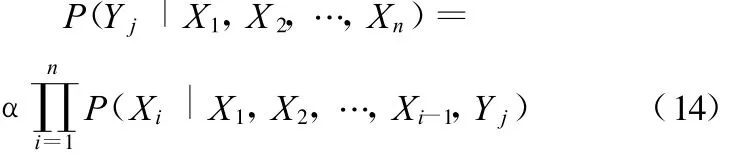
将式(14)代入式(9)中得

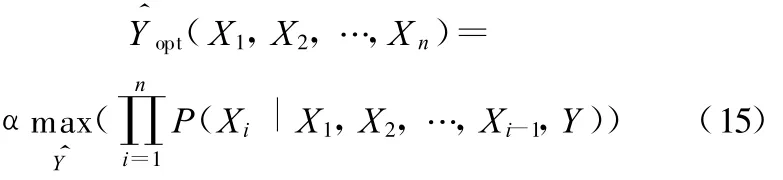
由此采用NB分类器,假定特征属性间相互条件独立,每个属性节点X i与故障类节点Y相关联,这种假定以指数级降低了贝叶斯网络构建的复杂性。因此式(15)又可以表示为[12]

通过式(16)计算出最大后验估计值,相对应的Y j类为诊断后得出的故障类型。

5 基于多特征信息融合贝叶斯网络的故障诊断方法

利用贝叶斯参数估计算法将故障特征进行有效融合,增加信息的完备性,为故障的正确诊断提供丰富、可靠的先验知识。利用贝叶斯网络方法构建特征与故障模式之间的联系,通过建立NB分类器消除故障特征模糊性的影响并简化信息融合结果。最后,通过最大后验概率估计值的比较得出诊断结论。诊断流程图如图2所示。

图2 故障诊断流程图

其诊断过程为：

(1)设计液压泵故障模式,在液压泵出油口安置振动传感器。利用试验平台采集各故障振动信号;

(2)对采集的信号进行小波消噪处理;

(4)利用贝叶斯参数估计的算法对故障特征信息进行多特征信息融合;

(5)根据故障特征信息与故障模式之间的联系,运用训练样本构建贝叶斯网络;

(6)通过贝叶斯网络建立NB分类器,对信息融合结果进行简化。并利用最大后验概率估计值的计算结果识别故障发生的类型。

6 实验分析

本实验是在材料试验机液压伺服系统试验平台上完成的,选取MCY14-1B型号轴向柱塞泵为研究对象,电机额定转速为1500r/min。对泵壳的振动信号进行采集。其试验台如图3所示。实验分三次进行。

图3 液压泵故障诊断试验台

6.1 第一次实验

人为设计轴向柱塞泵单柱塞脱靴故障和正常工作状态两种模式进行故障诊断分析。主溢流阀压力调定为15MPa,采样频率为1000Hz,每次采集时间为1s,采样1000个点。对采集的信号利用db5小波进行三层小波分析消噪处理,再利用db5小波进行六层小波包分解,提取出各频带能量信息表示的特征属性。从采样频率可知分析频率为500Hz,各能量特征对应的频带如表 1所示[13]。

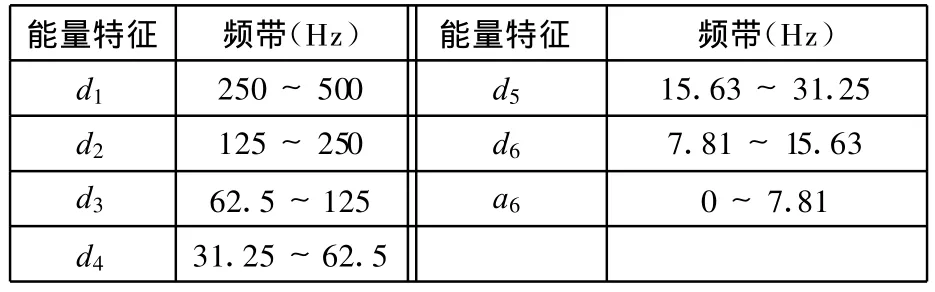
表1 能量特征对应的频带

选取110组数据作为试验样本,80组为训练样本(40组正常样本,40组故障样本),30组为测试样本(20组正常样本,10组故障样本)。将全部训练样本数据利用FCM算法进行聚类离散化处理[14],用训练样本构造贝叶斯网络,采用4.1节的知识建立NB分类器。其网络结构如图4所示。正常状态用Y1表示,脱靴故障用Y 2表示。

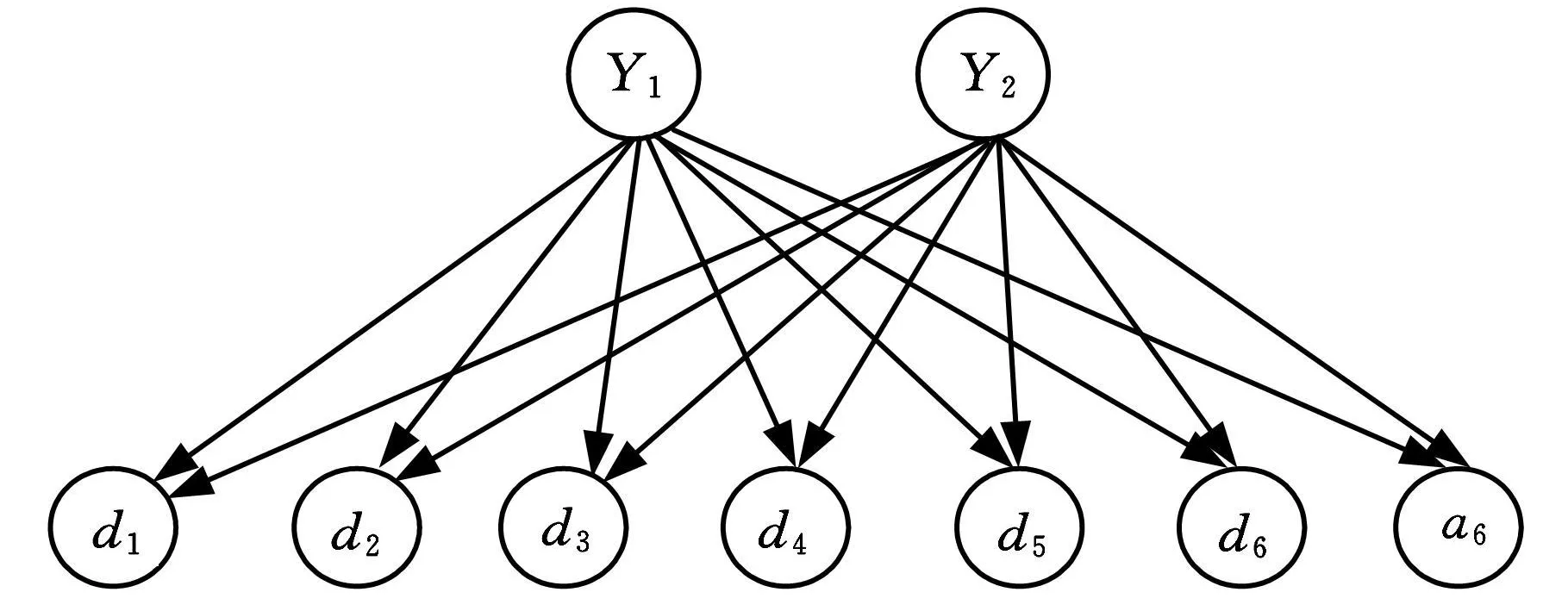
图4 两类故障的贝叶斯网络

利用其中一个状态为Y 1的测试样本{0,0,1,2,2,2,1}说明诊断过程。两种故障模式的先验概率取为P(Y1)=0.8,P(Y2)=0.2,其条件概率P(d i|Yj)和P(a6|Yj)(i=1,2,…,6,j=1,2)如表2所示。

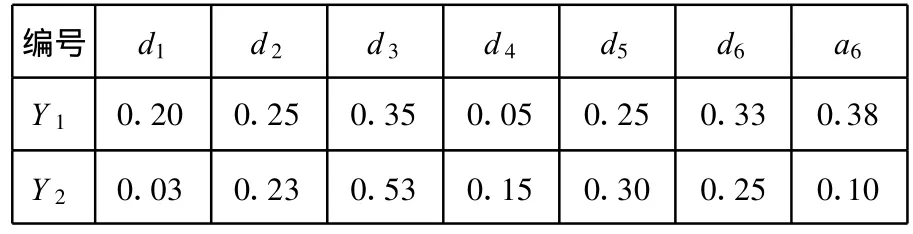
表2 各特征属性的条件概率

将得出的结果代入式(12)中得到g(y)=g1(y)-g2(y)=1.1669×10-5＞0,由此判断此样本为Y1状态样本,诊断结果与测试样本的状态相一致。

重复上述过程,对测试样本进行逐一验证,结果正常样本共19个诊断正确,1个诊断错误,正确率为95%,其中的10个故障样本全部诊断正确,确诊率为100%。这说明在只有两种故障模式的条件下,单从小波包分解的频域方面提取振动信号的故障特征,通过贝叶斯网络就能准确地诊断故障。

6.2 第二次实验

此次实验增加了轴向柱塞泵松靴的多种故障及配流盘磨损故障,其故障类型如表3所示。

表3 故障类型集

选取480组数据作为实验样本,其中320组为训练样本(每种故障类型有40组样本),160组为测试样本(每种故障类型有20组样本)。采用与第一次实验相同的特征提取方法,利用4.2节的多故障模式贝叶斯分类器故障诊断方法进行分析,中间计算过程略去,得到的诊断结果如表4所示。

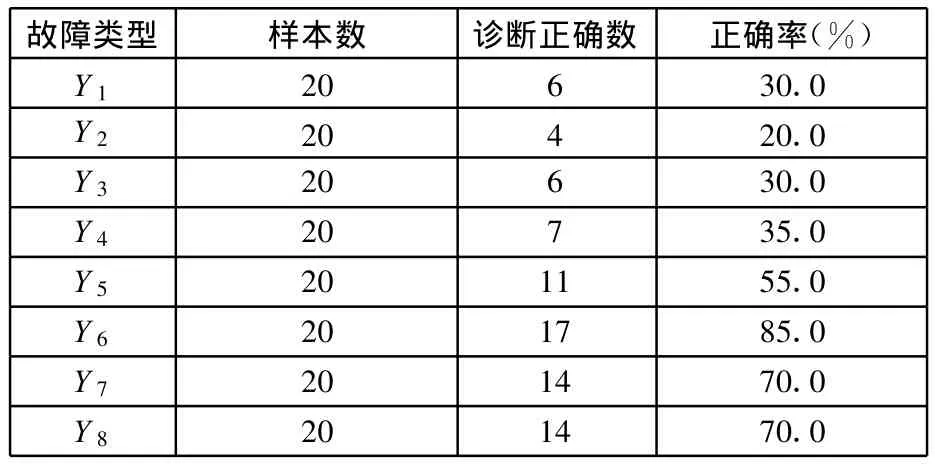
表4 各故障模式的检验结果

从表4中可以看出,增加故障模式后故障诊断的正确率明显下降。但是随着松靴柱塞数量的增加,诊断的正确率有显著的上升趋势。这说明松靴柱塞数量越多,故障与正常振动信号的频域特征区别越大。从以上分析来看,单从小波包分解的频域方面提取的故障特征信息存在明显的不完备性,综合故障诊断率低。当松靴柱塞增多时,虽然有故障特征模糊性的影响,但是贝叶斯网络的故障诊断方法仍然能得到较高的正确率,这充分说明贝叶斯网络方法能够有效地消除故障特征模糊性的影响。为消除特征信息不完备性的影响,提高综合诊断的正确率,下面采用多特征信息融合的方法进行实验。

6.3 第三次实验

本实验的故障模式选取与第二次实验相同(表3)。调定主溢流阀的压力为15MPa,采样频率为1000Hz,每次采样时间为1s。对采集的振动信号利用db5小波进行三层小波消噪处理。经第二次实验证实,利用第一次实验的特征提取方法不能满足对多故障模式的故障诊断要求,单从小波包分解获取的频域信息来反映多故障模式的状态是不完整的。如果从多方面获得振动传感器的多维特征信息加以综合利用,就能对系统进行更可靠更精确的监测与诊断。由此,本次实验从振动信号中提取小波包分解的频域和幅域共12个特征信息,将这些信息当作来自多个传感器的多源信息,通过贝叶斯参数估计算法将多特征信息进行有效的融合,融合过程如图5所示。

采用db5小波包进行六层分解得到各频带能量值表示的特征信息有：d 1～d 6能量特征,对应各层的高频细节,a6能量特征,对应第六层的低频逼近。

幅域量纲一参数表示的特征信息有[15]：

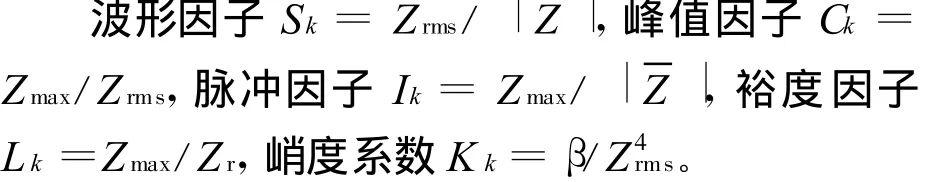
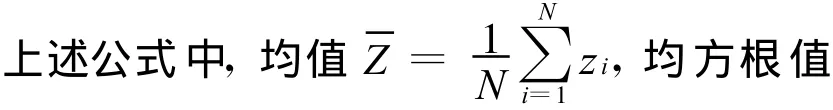
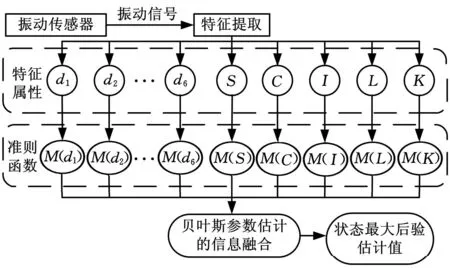
图5 信息融合框架图

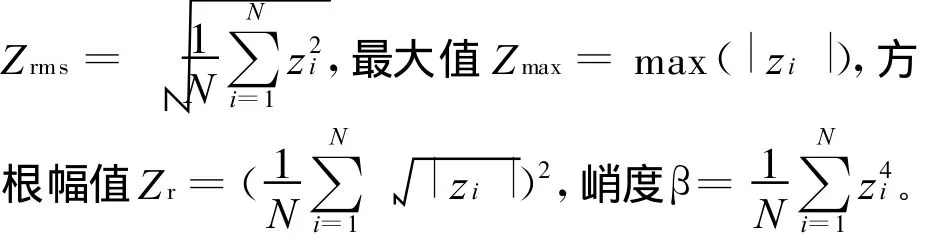
其中zi为离散随机信号的第i个采样点。量纲一参数 Sk、Ck、Ik、Lk和K k对应的特征属性分别为S 、C、I、L 和 K 。

利用上述特征提取过程得到每种故障类型60组样本,样本总数为480组。将全部样本通过FCM算法进行聚类离散化,每种故障类型取出40组作为训练样本,由此得到训练样本320组,其余160组作为测试样本。样本的部分信息如表 5所示。

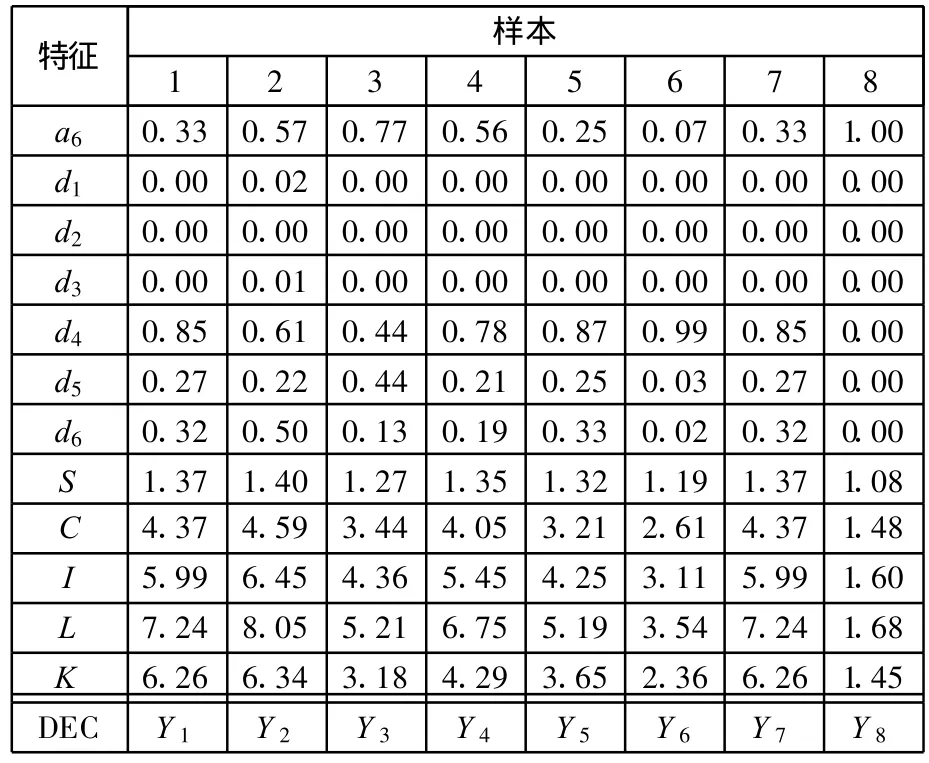
表5 部分样本信息表

首先,采用贝叶斯参数估计算法进行多特征信息融合;其次,利用构造的贝叶斯网络(图6)建立NB分类器,并简化信息融合结果;最后,用测试样本计算最大后验估计值对柱塞泵进行故障诊断检验。

其中某个故障类型为Y 3的测试样本{1,1,0,2,1,2,0,1,1,2,0,1}的诊断过程如下：由式(14)得

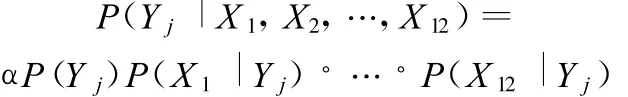
进而得到

图6 多类故障的贝叶斯网络

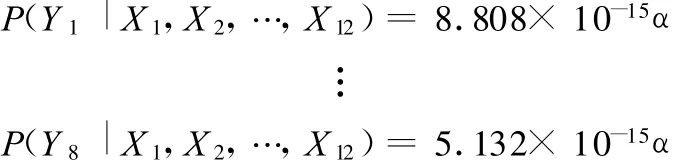
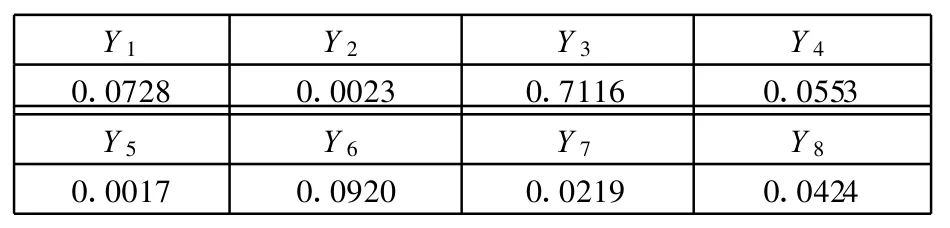
表6 各故障对应的后验概率

根据表6的数据,通过贝叶斯参数估计信息融合算法的简化结果式(16),计算出的最大后验估计值为Yˆopt(X 1,X2,…,X 12)=0.7116。由此可以确定此故障为Y3类,即两个柱塞松靴故障,诊断结果与测试样本的故障状态相一致。利用同样的方法,对其余样本进行测试得到的诊断结果如表7所示。

表7 各故障模式的检验结果

从表7的诊断结果可以看出,信息融合后的故障特征完备性得到了加强,诊断的正确率与未经过信息融合的故障诊断相比较有了大幅度提高。

6.4 实验的结果分析

从三次实验的结果来看,第一次实验单独从频域获取特征信息进行贝叶斯网络的故障诊断,能很好地区分两种故障模式。增加了故障模式后进行第二次实验,用第一次实验的方法判断故障,结果表明诊断正确率过低,不能满足故障诊断的要求。通过对前两次实验的比较可以断定：单独从频域方面进行特征提取,使得故障特征信息存在明显的不完备性。为此,在第三次实验中引入了多特征信息融合方法,从小波包分解的频域和幅域两方面获取振动传感器的多特征信息,并利用贝叶斯参数估计算法进行了有效融合,增加了故障特征信息的完备性。从实验的结果来看,故障诊断的正确率有了明显的提高。由此,验证了多特征信息融合的贝叶斯网络故障诊断方法对液压泵故障诊断的有效性。

7 结论

(1)针对柱塞泵的特点和检测条件提出了多特征信息融合技术与贝叶斯网络相结合的故障诊断方法。通过实验证明,这两种方法的结合能够消除液压泵故障特征模糊性和不完备性的影响。

(2)根据多源信息融合的广义定义,将振动信号的多个故障特征信息当作多个不同传感器的多源信息。提出了基于贝叶斯参数估计算法的多特征信息融合方法。

(3)实验结果表明,该方法能够对柱塞泵进行有效的故障诊断,并且可以推广到其他旋转机械的故障诊断中,具有较为广阔的应用前景。

[1] Niu Huifeng,Jiang Wanlu,Liu Siyuan.Research on the Hybrid Fault Diagnosis Approach Based on Artificial Immune Algorithm[C]//Proceedings of 4th International Conference on Natural Computation(ICNC'2008).Jinan,2008：667-670.

[2] 牛慧峰,姜万录.免疫支持向量机方法在液压泵故障诊断中的应用[J].中国机械工程,2008,19(14)：1736-1739.

[3] 刘思远,姜万录.粗糙集在液压泵故障诊断研究中的应用[J].机床与液压,2008,36(10)：196-198,204.

[4] Nilsson N.Artificial Intelligence,a New Synthesis[M].San Francisco：Morgan Kaufmann Publishers,1998.

[5] 韩崇昭,朱洪燕,段战胜,等.多元信息融合[M].北京：清华大学出版社,2006.

[6] 李宏坤,马孝江,王珍.基于多征兆信息融合理论的柴油机故障诊断[J].农业机械学报,2004,35(1)：121-124.

[7] 王少萍,苑中魁,杨光琴.液压泵信息融合故障诊断[J].中国机械工程,2005,16(4)：327-331.

[8] 姜万录.基于混沌性质和多分辨分析的故障诊断理论及试验研究：[D].秦皇岛：燕山大学,2001.

[9] 李俭川,胡茑庆,秦国军,等.贝叶斯网络理论及其在设备故障诊断中的应用[J].中国机械工程,2003,14(10)：896-900.

[10] Su Hong Sheng.Multi-source Fuzzy Information Fusion Method Based on Bayesian Optimal Classifier[J].Acta Automatica Sinica,2008,34(3)：282-287.

[11] 王玉珍.基于贝叶斯理论的分类模式挖掘方法研究[J].微型计算机应用,2007,28(6)：664-668.

[12] 朱永利,吴立增,李雪玉.贝叶斯分类器与粗糙集相结合的变压器综合故障诊断[J].中国电机工程学报,2005,25(10)：159-165.

[13] Liu Siyuan,Jiang Wanlu,Niu Huifeng.Fault Diagnosis of Hydraulic Pump Based on Rough Set and PCA Algorithm[C]//Proceedings of 5th International Conference on Fuzzy Systems and Knowledge Discovery.Jinan,2008：256-260.

[14] Bezdek J C.Pattern Recognition with Fuzzy Objective Function Algorithms[M].New York：Plenum Press,1981.

[15] 韩捷,张瑞林.旋转机械故障机理及诊断技术[M].北京：机械工业出版社,1997.