基于小波包分析和Elman网络的切削表面粗糙度预测方法
迟 军 陈廉清 杨超珍
宁波工程学院,宁波,315016
0 引言
根据经验或试验选用合理切削参数是传统的切削加工中保证表面粗糙度要求的主要方法。切削过程是动态的,材料的金相组织、硬度、韧性、切削振动等诸多影响表面粗糙度的因素在不断变化,在同一切削工序中采用统一的切削用量在兼顾加工质量和效率方面无法令人满意[1]。如果数控系统能根据加工状况实时预测表面粗糙度值,就可在线自动优化切削用量,大大减少加工过程中财力、人力和时间的浪费。
目前预测表面粗糙度值的方法有两大类:数学模型法和间接检测法。前者依靠传统数学模型计算表面粗糙度值,后者通过在线检测其他物理量来间接推算表面粗糙度值。数学模型法是建立在物理学关系或统计学关系上的[2-3],由于切削加工过程极为复杂,多种影响因素难以完全确定,因而不可能准确建立基于物理关系的数学模型。统计学模型能比较全面地反映切削过程的“共性”特点,但难以对每个切削过程“个性”作出准确估计,其缺点与传统的经验法相类似。间接检测法则是针对每个切削过程通过在线检测相关物理量,利用分析工具实时计算得出表面粗糙度值,最受重视的相关物理量是切削声的声强或声压[4-5]。此法在实验室中能达到满意效果,但在车间中,由于受相邻同类型机床切削声的干扰,其精度难以保证。切削力能反映表面质量,不少研究中将其作为相关物理量[6],但此方法的敏感度欠佳,预测效果差强人意。表面粗糙度的变化也可以通过切削振动的位移表达出来,且受同频机械振动的影响较小,亦适合作为相关物理量,但当前研究中检测位移的工具是电涡流传感器,它易受复杂电磁环境干扰,在实践中不易推广[7]。
考虑到加速度与位移间存在明确的数学关系,且压电加速度传感器抗电磁干扰能力强,所以本研究把切削振动加速度作为相关物理量,结合Elman网络和遗传算法,提出了利用遗传小波网络实时预测表面粗糙度的方法。
1 表面粗糙度预测的理论依据
理论界对于切削表面粗糙度的模型已经过多年研究,在已知切削速度v c、进给量 f、背吃刀量ap和修正系数 x、y、z、k的前提下,使用最广泛的模型为

此模型只能粗略估算表面粗糙度值,因为它只考虑了切削用量对表面粗糙度的影响,实际上因为刀具和工件之间的相对振动在切削表面造成的振痕亦直接影响表面粗糙度值。利用分形理论对影响表面粗糙度的因素进行分析,结果表明当在机床上实施切削时,若以影响表面粗糙度的各因素为子集Ai,取

则切削时振动的分维数高达1.89,这表明切削振动是除切削用量外影响粗糙度值的最主要因素[8-9]。不过,切削理论也表明,振动不能反映切削过程全貌[10]。
基于以上结论,本研究提出将传统的切削用量法与切削振动检测法结合起来实现表面粗糙度值的预测,其主要步骤如下:在车床上取不同切削参数,对不同尺寸的工件进行切削以获得振动加速度信号,离线检测工件被加工面的粗糙度值;构建用于预测粗糙度值的小波网络;把记录下的数据分成两组,分别用于训练和精度检验,研究结果验证了此方法的可行性。
2 遗传小波网络预测法
结合遗传算法的小波网络预测法是有效的预测工具。本研究中的小波网络结构分为两层:提取层和逼近层。
2.1 小波包改进算法
离散小波包分析是提取层的核心算法,它将切削振动信号从传感器输出信号中提取出来作为预测的重要依据,避免其被干扰信号淹没。传统的小波包算法通过待分析信号与相应的小波滤波器作卷积运算来实现分解与重构[11],时域中不存在真正的理想滤波器,切削振动也不是带限信号。在信号单支重构时,传统算法会造成信号在频域上的混叠。
本研究提取信号属于单支重构,因此引入CH和CG算子以改进传统算法、消除混叠带来的误差。设待过滤信号是 x(t),此信号共有m层,第m层共有n支分解信号,分解信号集合为{1,2,…,2i-1,2i,…,n},第m层的第n支分解信号可写为pnm(t),低通分解滤波器和高通分解滤波器分别是H(t)和G(t),低通重构滤波器和高通重构滤波器分别是h(t)和g(t),第m层的第n支重构信号可写为(t)。则分解算法为

而重构算法为
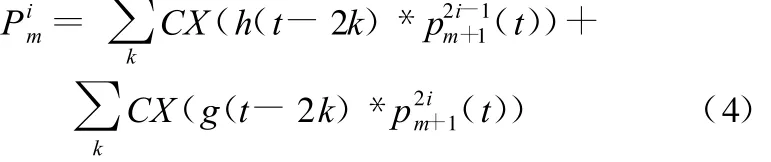

同理,CG算子的定义如下:
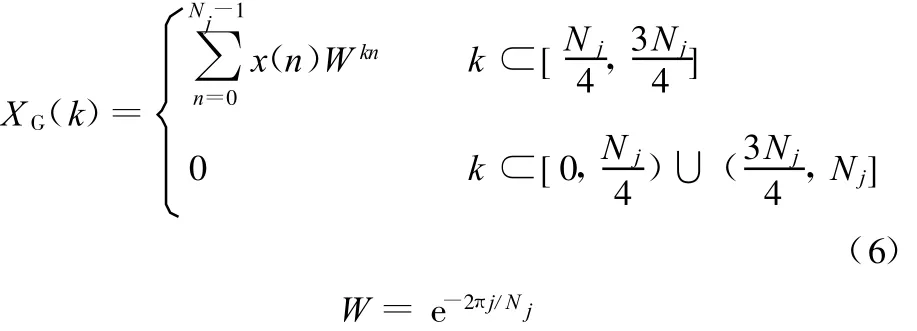
经此法滤波后的振动加速度信号才可进入逼近层作为预测的依据。
2.2 Elman网络算法
逼近层实现预测功能的核心算法是神经网络。传统神经网络中的主要逼近运算工具是BP(back propagation)算法[12],因为BP网络结构简单,便于构建和训练,但在切削过程中,机床会不断磨损,其振型也会逐渐改变。BP网络不能学习时间模式[13-14],无法适应这种改变,其推算精度会随着机床精度的下降而下降。本研究以Elman算法取代BP算法,这样神经网络就同时具有空间模式和时间模式的学习能力了[10]。
2.2.1 Elman网络结构及参数确定
设输入层和隐层的神经元数分别为r和u,且网络中第k个输入向量中第i个参数是p(i);隐层的传递函数是γ;输出层的传递函数是φ;输入层第i个神经元输出到隐层第j个神经元的权值是w i,j;与隐层第j个神经元对应的反馈权值是u j;与隐层第j个神经元的输入对应的阈值是b j;隐层第j个神经元到输出层神经元的权值和阈值分别是vj和dj,则与第k个输入向量对应的输出向量为
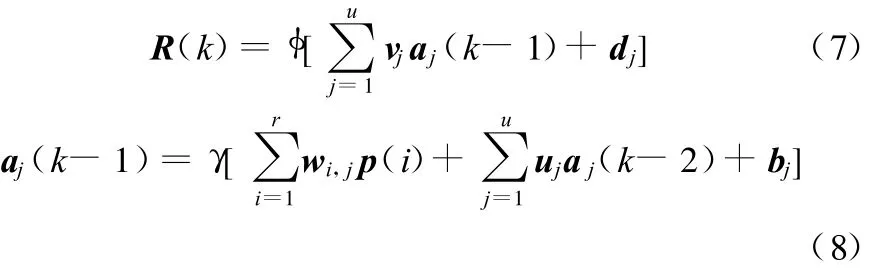
式中,aj(k-1)为与第k-1个输入向量对应的隐层第j个神经元的输出值。
表面粗糙度是区域测量值,不是点值,所以以0.1s为检测周期,计算出每个周期内从提取层输入到逼近层的振动加速度幅值的均值,并以连续的5个检测周期的均值m1~m5为一组,结合主轴转速n、进给速度 f和切削深度a p共同构建Elman算法的输入向量:(n,f,ap,m1,m2,m3,m4,m5)T。Elman网络的输入层取 8个神经元,预测层输出的是粗糙度值,故输出层只需一个神经元。隐层的神经元数量决定着预测层的精度和速度,若n h、n i、n o分别代表隐层、输入层和输出层的神经元数目,存在经验公式:
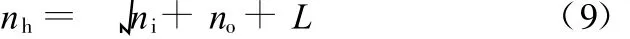
其中,L是0到10之间的整数,本研究取L为9,则隐层包含12个神经元。
2.2.2 网络参数的训练
为了避免Elman算法在训练时陷入局部极小[15],需先用遗传算法(GA)对网络参数进行优化[16],在解空间中定位出较理想的搜索空间,再利用Elman算法训练出最佳值,其流程如图1所示,主要步骤中的相关参数说明如下:

图1 GA-Elman网络训练流程图
(1)设定种群规模Q为80,随机选择实数的编码染色体,其基因数为待优化的网络参数的数量之和;
(2)第i个样本对应粗糙度预测值是Oi,实测值是Ei,则设定遗传算法的选择度函数为

(3)设定遗传代数是100,选择算子采用几何规划排序(选择率取0.1),交叉算子采用算术交叉(交叉率随机确定),变异算子采用非均匀变异。
与传统的 Elman算法相比,采用GAElman算法训练后的网络精度有明显提高,其对比效果见图2。

图2 使用遗传算法前后Elman网络相对误差的对比
2.3 小波网络预测流程
本研究的小波网络采用松散型结构,把输入信号空间变换成由Elman隐层输出所张成的空间,使得特殊特征提取准则最大化,在具有非线性逼近能力的同时,又有时频特征提取能力。预测算法的流程如图3所示。
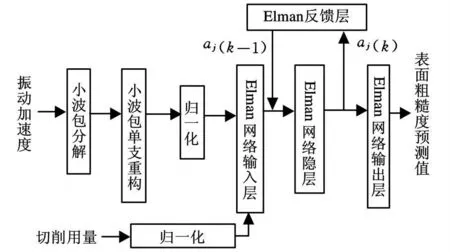
图3 表面粗糙度的小波网络预测算法流程
适用于提取层的小波包母函数有 Haar或Daubechies函数。Haar函数在研究中效果不佳,而不同阶的Daubechies函数实验结果表明,阶数大于10时,效果提升得并不明显,考虑到运算速度需要,取db10作为母函数,作3层分解,重构后取第2支作为预测的依据。Elman算法中的γ取tansig函数,φ取purelin函数,aj(0)取 0,学习率是0.7,动量因子为0.5,最大迭代次数是300,系统总误差设为0.001。
由于振动信号幅值在数值上与有些切削参数(如切削速度)相差太大(数量级大约相差 104倍)。实验表明,将数量级相差如此大的参数直接输入逼近层后,训练时难以收敛到目标精度,所以与通常的松散型小波网络不同,本研究中的数据必须先进行归一化操作后才能进入Elman网络进行训练和预测。
3 表面粗糙度预测实验
为验证本方法的可行性,组装如图4所示的实验装置。在 TK-40A数控车床刀架上安装CA-YD-107振动传感器,以不同的切削用量对长200mm不同直径的工件进行切削,以取得实验数据。工件的材料分别是铝6061和钢Q235。按以下流程进行实验操作:
(1)记录每次切削时的切削用量,并以4000Hz采样频率记录切削面法线方向的振动加速度;
图4 实验装置图
(2)用TR240表面粗糙度检测仪测量并记录加工面的粗糙度;
(3)把每组中的振动信号输入小波网络的提取层作3层小波包分析,取重构信号中的第2支,以0.1s为周期计算其振幅均值;
(4)将连续5个周期的均值与对应的切削用量和粗糙度值编组,得375组数据,分别作归一化处理;
(5)把其中的250组输入小波网络逼近层实施训练;
(6)训练完成后,检验其余125组输入小波网络逼近层的精度。部分数据如表1、表2所示,网络的预测结果与实测结果的对比如图5所示。
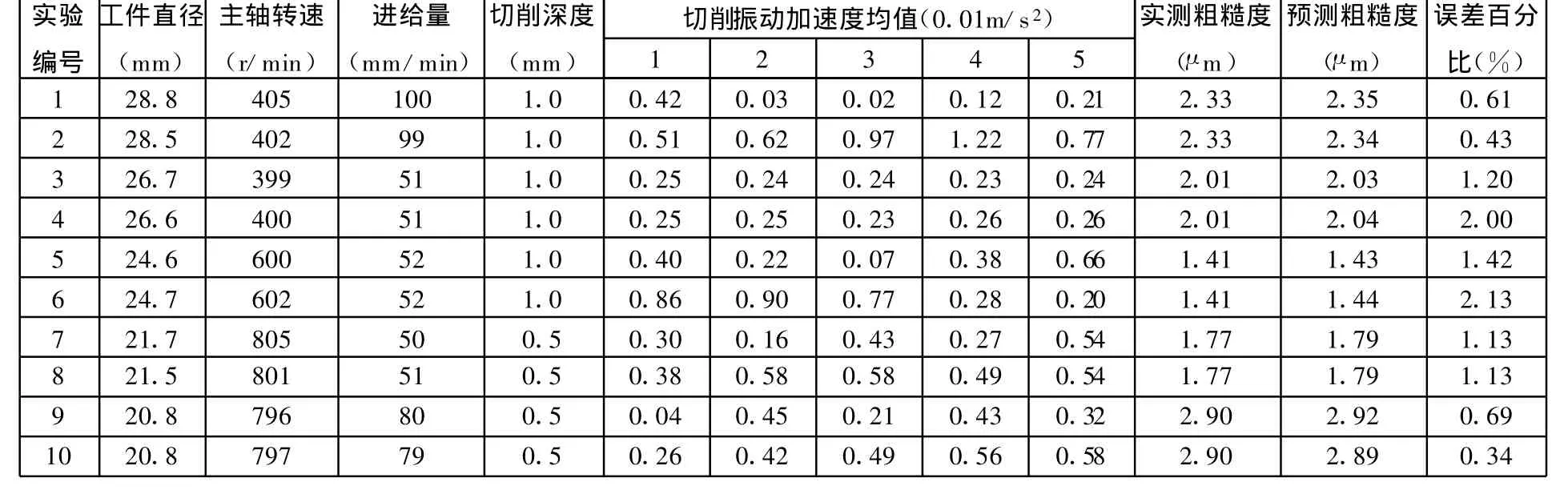
表1 用于表面粗糙度预测训练的铝6061材料的部分实验数据

表2 用于粗糙度预测训练的Q235材料的部分实验数据
实验结果表明,利用此方法预测的精度是比较令人满意的。误差的分布有一定的随机性,这与噪声干扰有关,也与加工的稳定性有关。持续切削时刀具的磨损、工件的形状尺寸及刚度会对误差带来一定影响,但均小于工件允许误差3%,上述结果验证了本文方法的有效性。

图5 遗传算法优化后Elman网络的计算结果与实际结果的对比
4 结论
(1)为实现车削过程中自动在线检测表面粗糙度的目标而提出了基于小波网络的在线检测方法。能够根据切削振动加速度的平均幅值和切削用量准确地预测出切削表面的粗糙度值,为现有的数控系统实现在线自动优化切削用量的新功能提供了理论基础。
(2)在Elman网络训练前,将其权重编码成染色体,利用遗传算法进行预先优化的措施明显提高了网络精度和收敛速度。
(3)本研究是在车床上开展的,对于铣削加工表面的粗糙度预测还需作进一步研究。
[1] 王洪祥,董申,李旦.通过切削参数的优选控制振动对超精密加工表面质量影响[J].中国机械工程,2000,11(4):452-455.
[2] 林岗,毛伟,马莉,等.基于振动传感器的车削加工表面粗糙度预测[J].组合机床与自动化加工技术,2007(9):51-56.
[3] Lin S Y,Cheng S H.Construction of a Surface Roughness Prediction Model for High Speed Machining[J].Mechanical Science and Technology,2007,10(21):1622-1629.
[4] Othman M O,Elkholy A H.Surface Roughness Measurement Using Dry Friction Noise[J].Experimental Mechanics,1990,30(9):309-311.
[5] 唐英,陈克兴,孙荣平.基于神经网络的表面粗糙度智能预测系统[J].机床与液压,1996(4):37-38.
[6] Singh D,Rao P V.A Surface Roughness Prediction Model for Hard Turning Process[J].Advanced Manufacturing Technology,2007,32(11/12):1115-1124.
[7] Salgado D R,Alonso F J.In-process Surface Roughness Prediction System Using Cutting Vibrations in Turning[J].Advanced Manufacturing Technology,2009,7(43):40-51.
[8] 李加种.金属切削动力学[M].杭州:浙江大学出版社,1993.
[9] 赵惠英,蒋庄德,田世杰.纳米级超精密切削表面粗糙度若干影响因素分析[J].机械工程学报,2004,40(4):190-194.
[10] Chern G L,Lee H J.Using Workpiece Vibration Cutting for Micro-drilling[J].Advanced Manufacturing Technology,2006,27(1):688-692.
[11] Ekici S,Yildirim S,Poyraz M.Energy and Entropy-based Feature Extraction for Locating Fault on Transmission Lines by Using Neural Network and Wavelet Packet Decomposition[J].Science Direct,2008,34:2937-2944.
[12] 张臣,周儒荣.基于BP神经网络的球头铣刀铣削力建模与仿真[J].中国机械工程,2005,16(20):1791-1794.
[13] Zhang JZ,Chen J C.The Development of an Inprocess Surface Roughness Adaptive Control System in Turning Operations[J].Intellectual Manufacturing,2007,18(6):301-311.
[14] Pal S K,Chakraborty D.Surface Roughness Prediction in Turning Using Artificial Neural Network[J].Neural Computation,2005,14(12):319-326.
[15] Quintana G,Garcia-Romeu M L.Surface Roughness Monitoring Application Based on Artificial Neural Networks for Ball-end Milling Operations[J].Intellectual Manufacturing,2009,16:219-240.
[16] Pendharkar P C.Genetic Algorithm Based Neural Network Approaches for Predicting Churn in Cellular Wireless Network Services[J].Expert Systems with Applications,2009,36:6714-6720.

