利用不均匀气隙优化自起动永磁电机的气隙磁密波形*
陈 超, 刘明基, 张 健, 陈伟华, 罗应立
(1.华北电力大学电气与电子工程学院,北京 102206;2.上海电科电机科技有限公司,上海 200063)
0 引言
自起动永磁同步电动机(Permanent Magnet Synchronous Motor,PMSM)与异步电机相比,具有效率高、功率因数高、功率密度高等优点,在一些长期连续运行的场合替代传统的异步电机具有较大的节能优势,因此得到研究人员越来越多的重视。目前,自起动PMSM多采用均匀气隙的结构,气隙磁场中含有大量谐波,使得电动势中谐波含量很大,增加了电机谐波电流和附加谐波铁损和铜损,影响电机效率的进一步提高[1],另外谐波磁场也会产生力矩波动,引起振动和噪声。长期以来,众多学者都对PMSM气隙磁密进行了优化设计,但大部分文献主要针对表面式磁体结构的永磁电机进行优化[2-7]。在文献[8]中作者采用Zooming算法对内置式永磁电机磁极不对称角度进行优化,以削弱齿槽转矩;杨玉波等研究了通过改变隔磁磁桥形状改变一个磁极的极弧宽度,进而削弱内置式PMSM齿槽转矩的方法[9]。文献[10]中运用智能型模拟退火算法,对开关磁阻电动机转子磁极几何形状进行了优化设计,在定、转子其他主要尺寸不变的条件下,使样机的静态转矩明显提高。文献[11]利用试算法对径向式V型磁体结构的永磁电机进行优化获得了气隙磁场波形畸变率与偏心距之间的关系曲线。文献[12]用B-样条参数化方法设计U形永磁磁路转子形状以减小电动势中的谐波。但是对于采用内置式磁路结构并且带起动导条的自起动PMSM磁极形状优化的文献并不多见。
本文运用有限元方法分析V型转子磁路结构的自起动PMSM的空载气隙磁密波形,利用遗传算法得到了最优偏心距,从而获得不均匀气隙永磁转子结构及气隙磁密波形,然后利用自主开发的时步有限元程序,分析对比了优化前后电机的电动势波形,最后通过试验间接验证了优化方法的有效性。
1 PMSM的结构及空载磁场分析
自起动PMSM的永磁体通常位于导条和轴之间的铁心中,笼型转子直接面向空气隙。本文计算模型源自某电机厂当前生产的电机,图1(a)为电机结构示意图,转子磁路采用V型结构,均匀气隙,笼型转子采用铸铝材料,具体结构参数如表1所示。测试中发现该电机的电动势和电流中的谐波含量较大。
为了考察永磁电机气隙磁场中谐波的影响,通常假定电机处于发电机状态,通过电动势波形反映谐波磁密对感应电动势的影响。假设磁路线性情况下,根据文献[13]的结果,定子开槽的影响仅仅使齿谐波电势增大或减小一定的倍数,假设能够消除由永磁转子引起磁场中的一切谐波,则即使定子开槽,亦不会引起电压波形的畸变。因此,本文在优化气隙磁场时暂不考虑定子开槽的影响,采用定子内表面光滑的模型[3],同时为了提高计算效率,只取电机的其中一个极距进行优化计算,优化采用的模型如图1(b)所示。
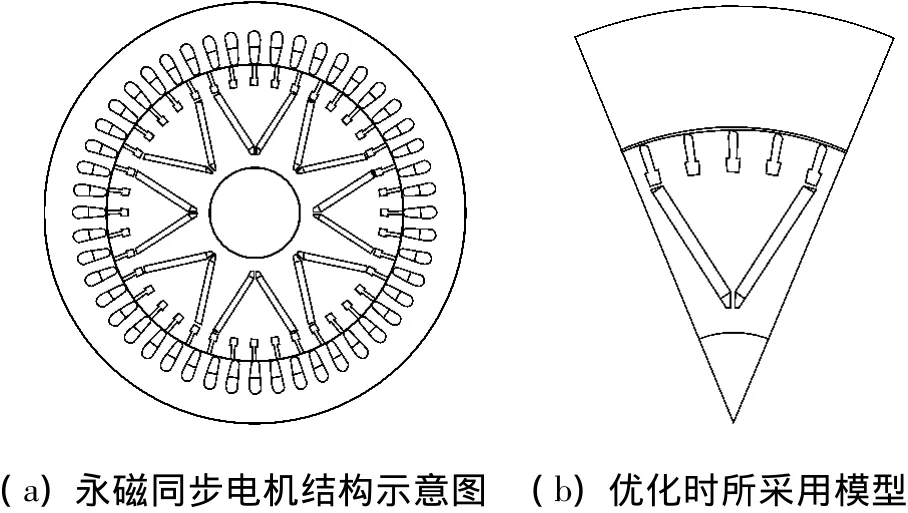
图1 永磁同步电机结构及优化模型
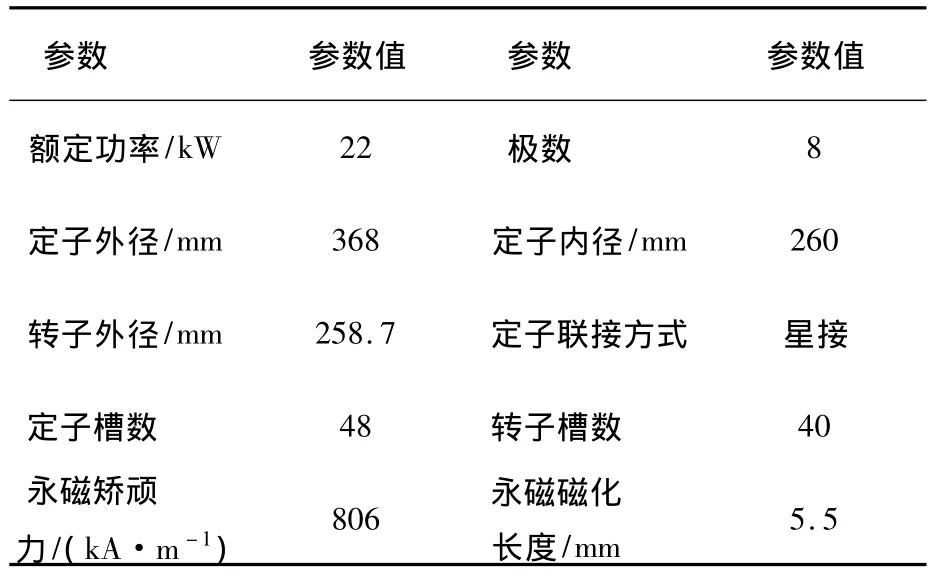
表1 自起动永磁电动机的主要参数
ANSYS是当前使用广泛、功能强大的有限元软件,其中的Electromagnetic模块提供电磁分析功能,可模拟电磁场分析。利用ANSYS进行有限元分析的基本流程为:建模—网格剖分—加载—求解—后处理。由此得到采用均匀气隙时PMSM一个极距下的空载气隙磁密波形,如图2(a)所示。对磁密波形进行谐波分析,可得到气隙磁密的基波和各次谐波幅值,如图2(b)所示,该气隙磁场含有丰富的谐波,谐波含量高达22.69%,这可能导致谐波电势、谐波电流、转矩脉动、振动噪声以及铁心损耗的增大[8-9]。

图2 均匀气隙时空载气隙磁场
2 磁极表面形状优化设计
对于均匀气隙的电机,转子外形是一个标准的外圆。为了改善气隙磁密波形,PMSM的偏心气隙结构设计如图3所示,在永磁体一个极距范围内,原来转子外形以O为圆心,而优化转子外形以O′为圆心,图3中以虚线表示,OO′即为需要优化的偏心距dm。为了更清晰的表示,将转子槽口部分放大显示如图3右半部分所示,其中虚线为优化后转子外形结构。
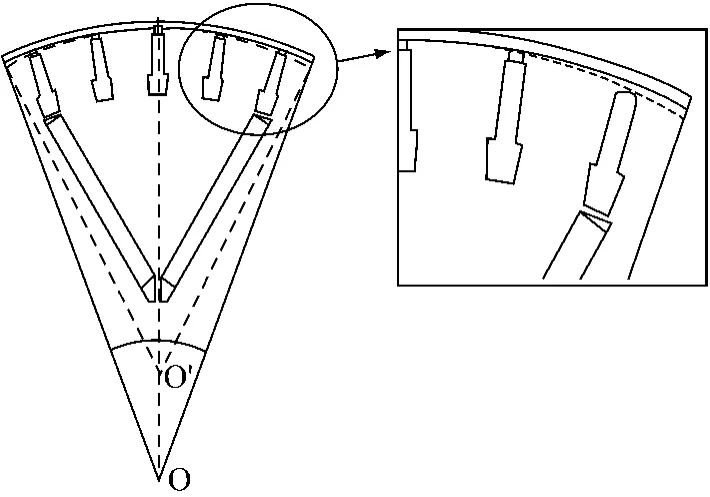
图3 永磁同步电机非均匀气隙结构图
3 遗传算法及气隙磁密波形优化
遗传算法是一种基于自然选择原理和自然遗传机制的搜索(寻优)算法,它模拟自然界中的生命进化机制,实现特定目标的优化。其基本思想是[15]:首先通过编码将问题空间映射到编码空间(如[0,1]),然后在编码空间内进行选择、交叉、变异三种遗传操作及其循环迭代操作,模拟生物遗传进化机制,搜索编码空间的最优解,最后逆映射到原问题空间,从而得到原问题的最优解。
采用遗传算法搜索最优偏心距的流程如图4所示,利用MATLAB进行数据的迭代优化,得出最优结果。图4中变量Gen表示遗传代数。
对图4所示流程图具体阐述如下。
(1)使用遗传算法需要的运行参数有:编码串长度bits、种群大小popsize、交叉概率Pc和变异概率Pm。编码串长度由设计变量的上界、下界及其搜索精度来确定。种群大小表示种群中所含个体的数量,群体越大则个体的多样性就越多,陷入局部解的可能性就越小,但计算效率会降低,一般取种群数目为20~100。交叉概率越高,产生新个体的概率越高,优良基因丢失速度也相应升高,一般取0.4~0.99。变异概率也是群体保持多样性的有效方法,一般取值为0.000 1~0.1。在本文中,各个参数取值分别为 bits=10,popsize=40,Pc=0.6,Pm=0.001。
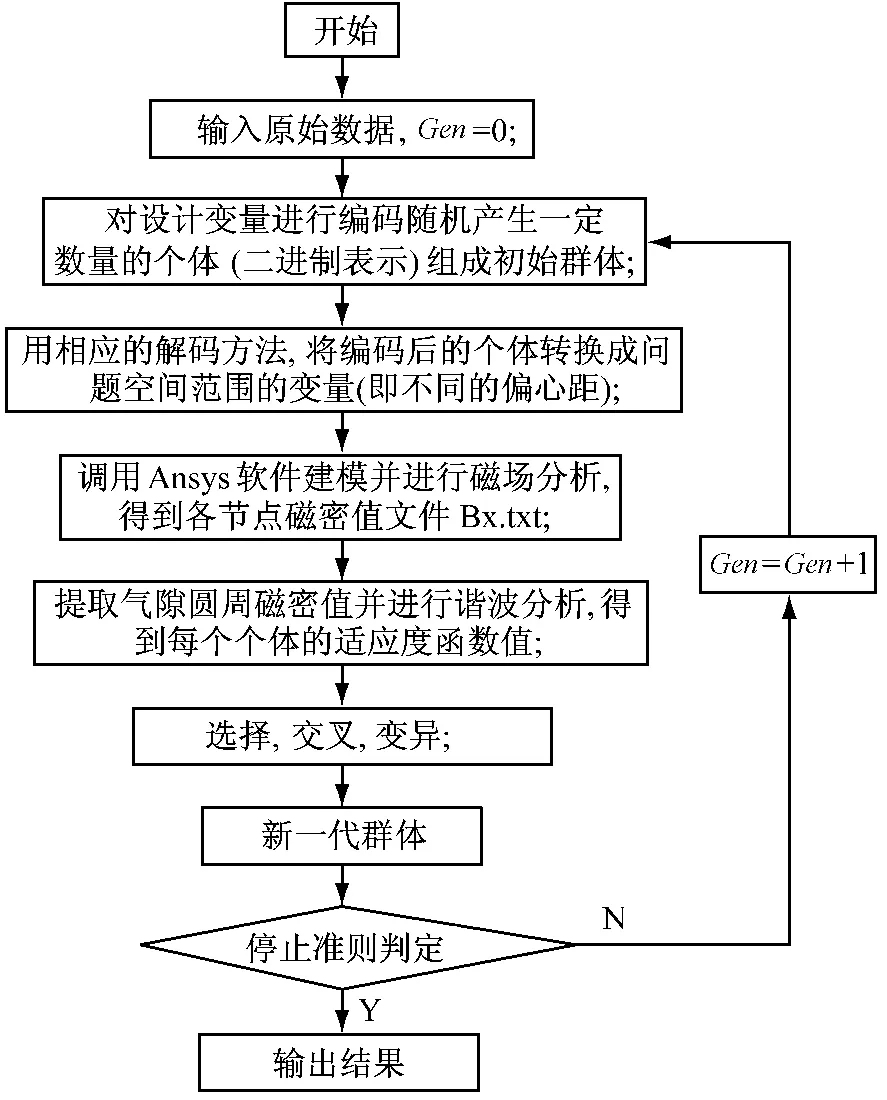
图4 遗传算法流程图
(2)编码:遗传算法不对优化问题的实际变量进行操作,需要把求解问题的可行解从其解空间转换到遗传算法所能处理的串结构数据搜索空间。本文采用常用的二进制编码,即用二进制数代表设计变量的取值,表示优化问题的一个可行解,也称为一个个体,在本文中为偏心距。
(3)以偏心距dm为设计变量,考虑到转子的槽口大小及机械强度和建立模型软件ANSYS的计算精度,设计变量的范围为0.7≤dm≤14 mm。
(4)ANSYS提供图形用户界面和命令流两种方式,命令流因其重塑性强,步骤简单,所以采用APDL语言进行命令流的编写,然后完成整个磁场的分析过程,得到各个节点的磁密值文件Bx.txt。
(5)适应度函数反映优化问题追求的目标,供遗传操作和评价个体时使用。本文中目标函数是空载气隙磁密的谐波含量最小,把一个求函数
最小值问题转化为求函数最大值问题,即从目标函数到适应度函数的变换,此时适应度函数F(x)和目标函数 f(x)有如下关系:F(x)=Cmaxf(x),其中,Cmax为输入常数,可以选取目标函数的最大值,此处选为100,即适应度函数:
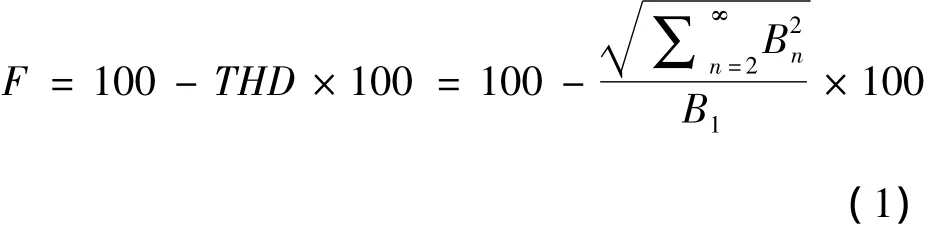
式中:n——谐波次数。
(6)遗传算法的三个算子:选择,交叉和变异。算子选择采用了最优保存策略和轮盘赌法[15],即首先找出当前群体的最优和最差个体,将最优个体保留并替换掉最差个体。为保证当前最优个体不被破坏,允许其不参与交叉和变异而直接进入下一代,然后将剩下的个体按轮盘赌进行选择。将这两种方法相结合的目的是:在遗传操作中,不仅能不断提高群体的平均适应值,而且能保证最优个体的适应值不减小。对于交叉,本文采用单点交叉的方式,交叉位的选取采用随机选择的方法。变异运算是产生新个体的辅助方法。经过选择、交叉和变异,产生新一代群体。
(7)遗传算法常采用的收敛判据有:规定遗传代数;连续几次得到的最优个体的适应值没有变化或变化很小等[15],本文中遗传代数N=50。经过多次迭代运算后,最优个体的适应度函数值保持稳定。当遗传算法停止执行时,可把当前代中最好的个体输出为计算结果。
在所有参数和法则确定后,对电机一个极距区域进行了优化求解。经过上述流程后求得的最优偏心距为13.68 mm,此时电机的空载气隙磁密波形及谐波含量分析分别如图5(a)、(b)所示。
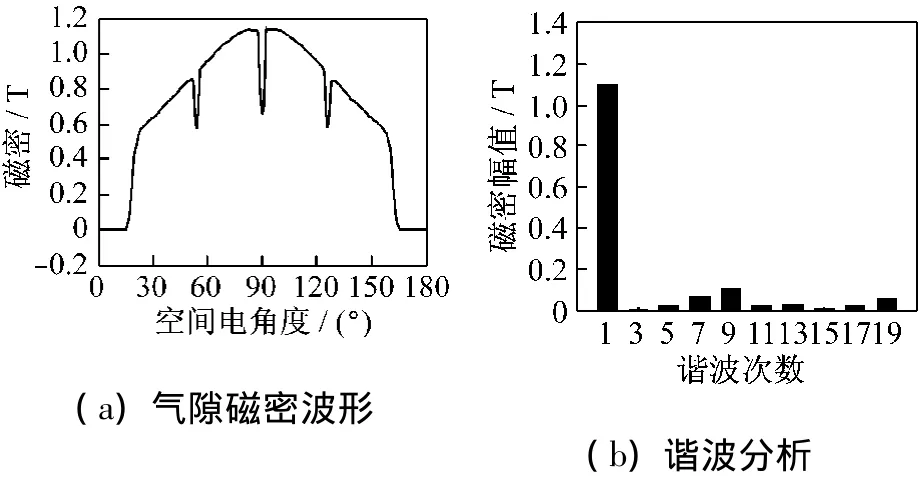
图5 非均匀气隙时空载气隙磁场
由谐波分析结果得到,采用偏心气隙后气隙磁密的THD为11.65%,比之前的22.69%明显降低,优化前后气隙磁密各次谐波对比如表2所示,可以看出磁极形状优化后除5次外气隙中各次谐波磁密明显降低。

表2 磁极优化前后气隙磁密谐波的分析对比 T
4 优化前后电动势波形计算及对比
为了考察磁极优化前后谐波磁密对电动势的影响,在考虑定子开槽并计及饱和的情况下,利用自主开发的时步有限元法计算程序,对优化前后的定子直槽电机的电动势波形进行分析对比。定子直槽时计算电动势波形如图6所示。由图6(b)的谐波分析可知,优化后的各次谐波电动势尤其是一阶齿谐波(这里为11、13次)明显降低。
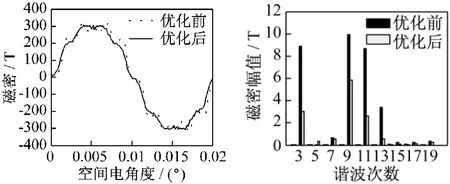
图6 磁极优化前后电机直槽计算的电动势波形比较
进一步计算对比磁极形状优化前后定子斜槽永磁电机的电动势,计算电动势波形及其谐波分析如图7所示,各次谐波电动势对比如表3所示。
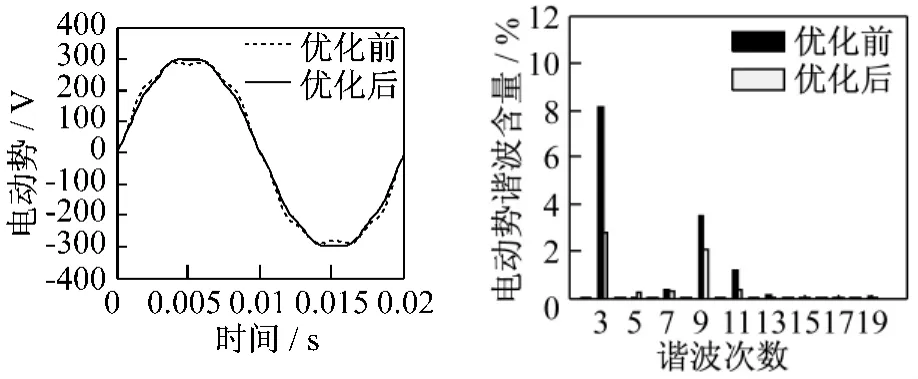
图7 磁极优化前后电机斜槽的计算电动势波形比较
由图7和表3可看出,优化后电动势谐波明显低于优化前的永磁电机电动势中的谐波。
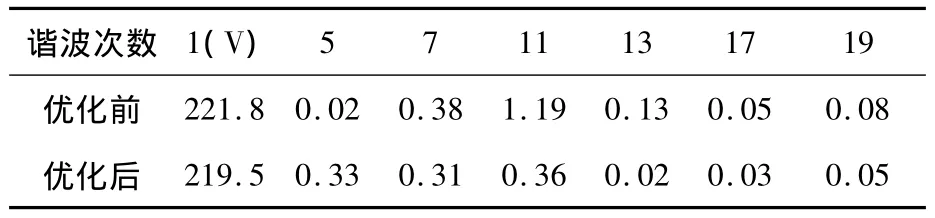
表3 磁极优化前后定子斜槽计算电动势谐波对比 %
5 试验验证
对优化前永磁电机作为发电机空载运行进行试验,测试得到空载相电动势数据,如图8虚线所示,并与通过时步有限元计算得到的电动势波形进行比较,从图8中可以看出实测曲线与计算曲线基本吻合。经谐波分析,时步有限元计算的相电动势基波有效值为221.8 V,与实测的222.3 V相比,误差为 0.22%;计算电势谐波含量为8.96%,与实测结果9.88%相差0.93%。实测与计算电动势中所关心的谐波含量如表4所示。从图8和表4可以看出,时步有限元计算结果比较接近样机试验测试的电动势波形,从而间接验证了前文中计算均匀和不均匀气隙结构永磁电机电动势的准确性和本文所采用优化方法的正确性。
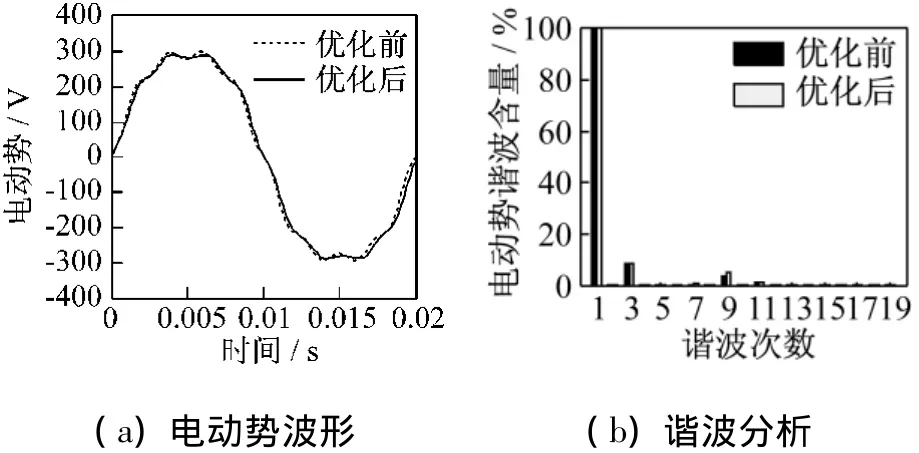
图8 磁极优化前电动势计算结果与实测对比

表4 时步有限元计算与实测电动势谐波分析对比 %
6 结语
为改善PMSM的气隙磁密波形,减少谐波含量,从而降低铁耗、提高永磁电机效率并减小转矩脉动,利用不均匀气隙结构改善空载气隙磁密波形,并采用遗传算法得出最优偏心距。通过优化前后空载气隙磁密及电动势波形的比较可看出,采用不均匀气隙的方法能有效改善PMSM气隙磁密波形,试验结果验证了气隙磁密波形优化的有效性。
[1]唐任远.现代永磁电机理论与设计[M].北京:机械工业出版社,2005.
[2]Hyuk Nam,Kyung-Ho Ha,Jeong-Jong Lee,et al.A study on iron loss analysis method considering the harmonics of the flux density waveform using iron loss curves tested on Epstein samples[J].IEEE transactions on magnetics,2003,39(3):1472-1475.
[3]Yong Li,Jingwei Xing,Tianbao Wang,et al.Programmable design of magnet shape for permanentmagnet synchronous motors with sinusoidal back EMF waveforms[J].IEEE transactions on magnetics,2008,44(9):2163-2167.
[4]Ping Zheng,Jing Zhao,Jianqun Han,et al.Optimization of the magnetic pole shape of a permanent-magnet synchronous motor[J].IEEE Transactions on Magnetics,2007,43(6):2531-2533.
[5]ChaithongsukS,Takorabet N,Meibody Tabar F.On the use of pulse width modulation method for the elimination of flux density harmonics in the air-gap of surface PM motors[J].IEEE Transactions on Magnetics,2009,45(3):1736-1739.
[6]孙立志,张弓,赵红茹,等.遗传算法在永磁电机气隙磁场设计中的应用[J].哈尔滨工业大学学报,2000,32(1):71-74,77.
[7]HsiehFu Min,Hsu Yu Sheng.An investigation on influence of magnet arc shaping upon back electromotive force waveformsfordesign ofpermanent-magnet brushless motors[J].IEEE Transactions on Magnetics,2005,41(10):3949-3951.
[8]王道涵,王秀和,丁婷婷,等.基于磁极不对称角度优化的内置式永磁无刷直流电动机齿槽转矩削弱方法[J].中国电机工程学报,2008,28(9):66-70.
[9]杨玉波,王秀和,丁婷婷.基于单一磁极宽度变化的内置式永磁同步电动机齿槽转矩削弱方法[J].电工技术学报,2009,24(7):41-45.
[10]白凤仙,邵玉槐,孙建中.利用智能型模拟退火算法进行开关磁阻电机磁极几何形状的优化[J].中国电机工程学报,2003,23(1):126-131.
[11]XuYing Lei,Li Qun Zhan,He Sheng Zhong.Simulation analysis of eccentricity of permanent magnet synchronous motor[C]∥ International Conference on Communications,Circuits and Systems,2009.ICCCAS 2009:749-752.
[12]JoonHo Lee,Dong Hun Kim,Il Han Park.Minimization of higher back-EMF harmonics in permanent magnet motor using shape design sensitivity with B-spline parameterization[J].IEEE Transactions on Magnetics,2003,39(3):1269-1272.
[13]汤藴璆,史乃,沈文豹.电机理论与运行(下册)[M].水利电力出版社,北京,1983.
[14]王秀和,杨玉波,朱常青.异步起动永磁同步电动机——理论、设计与测试[M].北京:机械工业出版社,2009.
[15]刘国华,包宏,李文超.用MATLAB实现遗传算法程序[J].计算机应用研究,2001:80-82.

