自控原理教学中的根轨迹方程及其数学矢量分析
于莲芝
(上海理工大学 光电信息与计算机工程学院,上海 200093)
自控原理教学中的根轨迹方程及其数学矢量分析
于莲芝
(上海理工大学 光电信息与计算机工程学院,上海 200093)
自动控制理论是研究自动控制共同规律的技术科学,教好这门课,使学生深入理解和掌握本课程具有重大意义。根轨迹法是古典控制理论中对系统进行分析和综合的基本方法之一,由推导出的根轨迹方程可知, 根轨迹方程中开环的零点和开环极点均为系统的特征根,本文分析了根轨迹在系统性能分析中的原理应用及特点,并对根轨迹方程进行了详细的矢量分析,使学生更深入清晰理解和掌握自动控制理论中的控制系统的根轨迹分析法,为自控原理教学提供参考。
自动控制原理;根轨迹;矢量
一、引 言
自动控制理论是各工科院校许多专业必修的主干课程,是一门理论性较强涉及数学、物理、电子等多学科专业领域专业课程,教好这门课和学好这门课要求教师和学生必须有所涉及学科课程的深厚的理论基础,因此,学好这门课,能深入理解和掌握本门课程对教师和学生都是一种严峻的挑战。自动控制理论是研究自动控制共同规律的技术科学,以传递函数为基础的经典控制理论主要研究单输入、单输出、线性定常系统的分析和设计问题。尽管自动控制系统有不同的类型,对每个系统也都有不同的特殊要求,但对于各类系统来说,在已知系统的结构和参数时,人们感兴趣的都是系统在某种典型输入信号作用下,其被控量变化的全过程,且对每一类系统被控量变化全过程提出的共同基本要求都是一样的,可以归结为稳定性、快速性和准确性,即稳、快、准。稳定性是保证控制系统正常工作的先决条件, 从时域角度讲控制系统稳定的充要条件是线性控制系统在初始扰动阶跃信号作用下, 其输出响应随着时间的推移逐渐衰减并趋向于零。也既是系统特征方程的所有根都具有负实部,或者说,系统传递函数的极点均在根平面的左半 S 复数开平面上(不包括虚轴)。
根轨迹是一种图解方法,它是古典控制理论中对系统进行分析和综合的基本方法之一。1948年EVANS提出了根轨迹法,该方法不需要求解闭环系统的特征方程,只需依据开环传递函数便可绘制出系统特征根随某一参数变化的轨迹图。本文分析了根轨迹在分析系统性能中的应用原理及特点,对根轨迹方程进行了详细的矢量分析,供教学参考。
二、根轨迹分析法
根轨迹是开环系统某一参数由零变化到无穷时,闭环系统特征方程的根(即闭环极点)在S平面上的变化轨迹。由根轨迹图直观地描述了系统特征方程的根(即系统的闭环极点)在S平面上的分布,因此,用根轨迹法分析控制系统十分方便,特别是对于高阶系统和多回路系统,应用根轨迹法比用其他方法更为方便,因此在工程实践中获得了广泛应用。实际控制系统往往是高阶的,即其闭环特征方程是S的高阶代数方程,当系统中某环节的某个参数发生变化,或为改善系统的控制性能而改变系统中某环节的某个参数时,系统的闭环极点也即闭环特征方程的根也发生相应的变化,而闭环系统的控制性能与闭环极点在极点平面上的位置有密切的联系。这就需要事先从理论上分析闭环极点随某个参数变化时在极点平面上的变化趋势从而得出某个参数的变化对系统性能的影响程度,作出理论上的指导。
三、根轨迹方程及矢量分析
1.根轨迹方程
根轨迹的概念描述为:当系统中某个(或几个)参数从0到+∞连续变化时,系统闭环特征方程的根(即闭环极点)在根平面(S平面)上连续移动而形成的轨迹,称为系统的根轨迹。闭环控制系统的一般结构图如下所示:

图1 一般控制系统结构
Fig.1 The common structure of the control system
则系统的开环传递函数为:
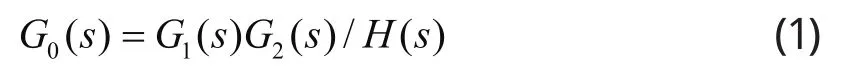
由于开环传递函数是各个环节传递函数的乘积形式,由于系统中各个环节一般为典型环节,而典型环节的传递函数一般不超过二阶,其分子和分母的S多项式极易因式分解,从而开环传递函数的零极点也容易获得。因此,闭环系统的开环传递函数可表为:
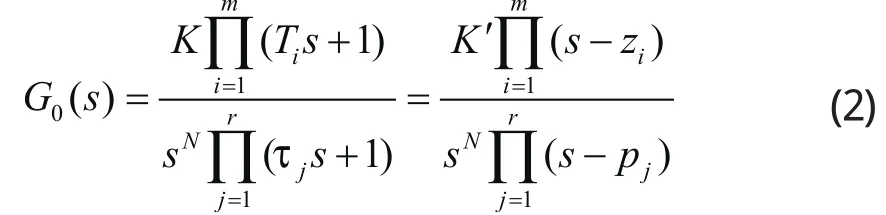
式中Zi是G0(S)的零点, i=1,2,….m, Pj是G0(S)的非零极点,sN表示有N个数值为0的极点, 且N+ r=n,n为系统的阶数。K叫开环系统的增益, K’叫开环系统的根轨迹增益,K与K’的本质相同,仅它们间的值有一系数关系,即:

式(5)、(6)也既为根轨迹方程。
2.数学矢量分析
根轨迹方程实质上是一个矢量方程,直接应用不方便,所以化为幅值方程和相角方程。
因为:
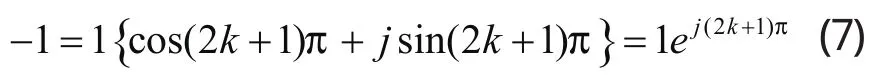
其中k=0,±1,±2, ……
式(6)中矢量s−zi在复平面s中的矢量表示为:
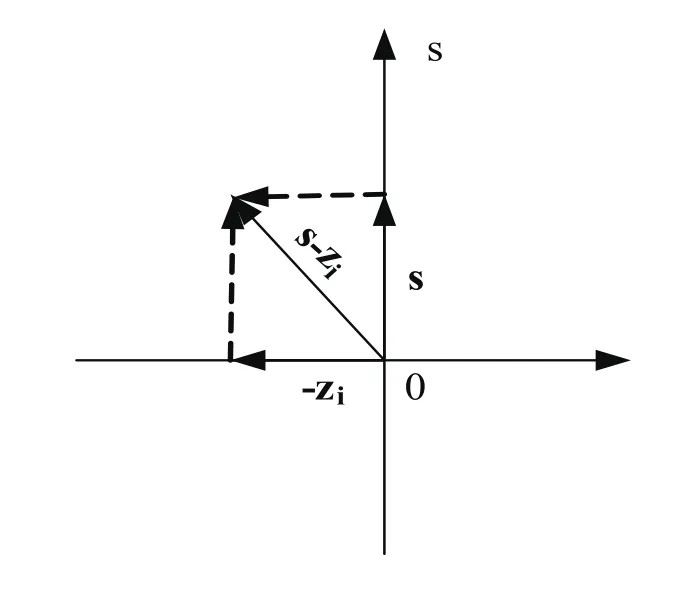
图2 开环零(极)点矢量示意图
Fig.2 The graph of open loop zero(pole)

式(7) 分解为幅值方程为:

在S平面上凡满足相角条件的点一定是闭环极点,即是闭环特征方程的根,凡不满足相角条件的点一定不是闭环极点,因此相角条件是绘制根轨迹的充分必要条件,根轨迹上某一点对应的K’的值可由幅值条件求出。
四、结 论
通过以上分析可知,根轨迹方程是一矢量方程,通过对根轨迹方程进行数学矢量分析将根轨迹方程转化为根轨迹幅值方程和根轨迹相角方程,相角条件是绘制根轨迹的充分必要条件,根轨迹方程中的开坏的零点和开环极点均为系统的特征根,通过系统的开环零、极点就可绘制系统闭环极点的随某一控制参数的变化轨迹,从而达到分析系统性能的目的。
[1] 胡寿松.自动控制原理(第四版). 科学出版社,2005.8
[2] 胡寿松.自动控制原理简明教程(第二版). 科学出版社,2007.10
[3] http://hi.baidu.com/zhaolinger_789/b log/item/ 7f1559f23d9edd58352acc5c.htm l
The Root Locul Equation and its Analysis of Mathematics Vectors in Teaching of Autocontrol Theory
Yu Lian-zhi
(College of Optoelectric Information and Computer Engineering, University of Shanghai for Science and Technology, Shanghai 200093)
Autocontrol theory is technique science to study the universal autocontrol laws. It is very important for teaching this course well and to make student understand it more thoroughly. Root locul is one of the basic methods of analyzing and synthesizing the system in classical control theory. From the root locul equation, the open loop zeros and the open loop poles are all the roots of the characteristic equation. This paper described the application theory and the characteristics of root locul during analysis of the system control performance, and the mathematics vectors in root locul equation were analyzed in detail. It provides the reference for the teaching of aotocontrol theory and for the students to understand and master the root locul method clearly.
Autocontrol theory, root locul, vectors

