基于Weil对的椭圆曲线数字签名方案
田润芙,杨 旭
(1.张家口职业技术学院,河北张家口 075051;2.河北宣化县交通局,河北张家口 075100)
0 引言
数字签名是一种重要的信息安全技术,随着椭圆曲线在密码学中的应用,人们对其进行了大量研究,发现作为一种公钥密码,椭圆曲线密码不仅有比较高的安全性,而且利用椭圆曲线离散对数问题可以构造三种基本形式的公钥体制,即数字签名体制、公钥加密体制和密钥交换协议等。1985年ElGamal提出了基于离散对数问题的数字签名方案,随后对ElGamal方案的变形和改进方案相继被提出,这些方案统称为ElGamal型数字签名方案。1994年Harn.L.和Xu.Y.提出了设计ElGamal型数字签名的规则,并列出了18种安全的ElGamal型数字签名方案。[1]本文在遵循这些规则的前提下,给出了另外一种签名方案。这种数字签名体制是通过基于ElGamal的椭圆曲线数字签名实现,通过Weil对来验证的。
1 基本知识与相关概念
1.1 Weil对及其相关概念
1.1.1 相关概念
定义1:设φ:E→E是椭圆曲线E上的一个非常数有理映射,P是E上一点,有理函数u是E在φ(P)点上的一致参数,称u∘φ在P点的阶数为φ在P点的分歧指数(RamificationIndex),记作eφ(P)=OrdP(u∘φ) 。
eφ(P)与u的选取无关。因为u是E在eφ(P)点的一致参数,所以P是u°φ的零点,故eφ(P)≥1。特别地,如果φ是一个自同态,那么每一点的分歧指数都相同,故可以记作eφ。
定义2:设φ:E→E是椭圆曲线E上的一个非常数有理映射,可如下定义除子群Div(E)上的自同态:
φ*:Div(E)→Div(E)
对任意的非零有理函数r,下式成立,
div(r∘φ)=φ*(div(r))
Weil对的定义:Weil对em是如下定义的一个二元函数:
em:E[m]×E[m]→μm
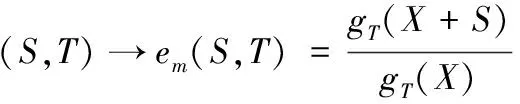
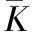
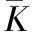
1.1.2Weil对具有的性质:
(1)双线性:(i)对任意的S1,S2,T∈E[m],em(S1+S2,T)=em(S1,T)em(S2,T)
(ii)对任意的S,H1,H2∈E[m],em(S,H1+H2)=em(S,H1)em(S,H2),
(2)恒等性:对任意的S∈E[m],em(S,S)=1
(3)对称性:对任意的P,Q∈E[m],em(nP,Q)=em(P,Q)n,em(P,nQ)=em(P,Q)n
(4)非退化性:如果任意的S∈E[m],那么em(S,O)=1;如果em(S,T)=1对于所有的T∈E[m],那么S=O。
(5)对于所有的S1,S2∈E[m],如果E[m]⊆E(Fqk),那么em(S1,S2)∈Fqk。
1.2 椭圆曲线上的ElGamal公钥体制
1.2.1 椭圆曲线离散对数问题
令E(F)为有限域F上的一条椭圆曲线,点P∈E(F),对于随机生成一个整数d,容易计算Q=d×P,但给定Q和P计算d就相对困难,即为椭圆曲线离散对数问题(ECDLP)。椭圆曲线密码体制的依据就是利用定义在曲线群上的离散对数问题的难解性。
设P是椭圆曲线E上的一点,若存在最小的正整数n,使得nP=O,其中O是无群远点,则称n是点P的阶。
1.2.2 椭圆曲线上的ElGamal公钥体制
设m|Pm是明文空间到椭圆曲线的嵌入,G∈E为椭圆曲线上的基点,G的阶为q。用户B欲向A发送信息m,则A选取dA(0 设p,Fq,q,l,μl均和前面1.1中Weil配对定义的意义相同(为了和明文m区别,把下标m改为l),P∈μl是E(Fq)上阶数为l的点。基于离散对数的难解性,用户A和B利用椭圆曲线的ElGamal公钥体制和Weil对进行签名以及验证。 ⑴用户A和B都将自己的公钥公开登记,用来作为双方和第三方(如:仲裁者)验证签名的依据。 ⑵将密码信息m用哈希算法求得数字摘要e,e=h(m),将e嵌入到椭圆曲线上,记为点Pe。 (i) 由Weil对的对称性可知:em(nP,Q)=em(P,Q)n=em(P,nQ)。 (ii)据双线性和对称性二性质,可得,对em(Y,G)的验证如下: em(Y,G)=em(dA(Pe+X),G)=em(Pe+X,dAG)=em(Pe+X,PA)=em(PePA)em(XPA)即Verk(Pe,X,Y)=true⟺em(Y,G)=em(PePA)em(XPA)。若等式成立,则接受(X,Y)是A的签名,否则拒绝。同理,B也可以采用同样的方式进行签名。A收到后,同样进行验证签名。 本数字签名方案是基于椭圆曲线离散对数问题,同时结合BDH问题,以及ElGamal类加密体制和签名方案而构造的。就其安全性分析如下: (1)由椭圆曲线密码的基础知识可知:在椭圆曲线中,当设Q=nP,P、Q∈E(F),从n、P求Q存在有效的算法,而从P、Q求n没有有效的算法,这个问题就称为椭圆曲线离散对数问题。从而,增强了方案的安全性。另外,由于本签名方案是基于椭圆曲线数字签名体制的签名方案,因此,具有椭圆曲线的特点:(i)安全性高,(ii)密钥量小,(iii)存储量小、传输时间短,(iv)灵活性好,只要有限域已定,其上的循环群就确定了等优点。 (2)本签名方案的安全性同时又基于双线性Diffie-Hellman(BDH)问题:已知P、Q、R∈E(Fq),求点S∈E(Fq),使得等式em(S,P)=em(R,Q)成立。攻击者想伪造签名,相当于求解BDH问题,该问题目前还没有有效的算法。因此,相信该问题是难以计算的。 (3)本签名方案为了增强安全性没有直接把明文m嵌入到椭圆曲线上,即点Pm,而是使用较为安全的Hash函数h(m),然后嵌入到椭圆曲线上后再进行签名。这样把Hash函数应用于数字签名中,从而也可以提高签名的速度。 (4)另外,本方案没有完全按照一般的ElGamal公钥体制进行签名。若签名按照一般的ElGamal公钥体制,其形式为:Sigk(Pm,k,dA)=(X,Y),其中X=kG,Y=Pm+dAX。但是攻击者可以用Y-Pm计算出dAX,然后用其他的消息得到P'm进行签名: X'←X,Y' ←P'm+(Y-Pm) 显然,这样的签名可以通过验证,于是签名很容易被伪造了。本方案由于dA很难计算,也就很难伪造Y,从而增强了方案的安全性。 本文提出了基于Weil对的椭圆曲线数字签名方案,并利用了ElGamal 型数字签名规则,使其安全性基于离散对数的难解性和BDH问题的难解性,具有较高的安全性。同时,也为解决椭圆曲线上数字签名的验证提供了一种新的方法。 参考文献: [1]Harn . L. and Xu . Y. ,Design of generalized ElGamal type digital signature schemes based on discrete logarithm , Electron Lettt ,1994 ,30(24):2025 - 2026. [2]赵云峰 等.一个基于Weil对的基于身份的群签名方案[J]. 计算机应用研究,2005,(5):124-125. [3]D JOHNSON,A MENEZES VANSTONE. The elliptic curve digital signature algorithm (ECDSA)[J].International Journal on Information Security,2001;(1):36-63. [4]Dr Tsuyoshi Takagi. Efficient Algorithms for Pairing-Based Cryptosystems. Marcus Stogbauer, 2004-01.2 基于Weil对的椭圆曲线数字签名方案

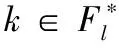
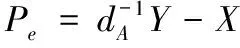
3 安全性分析
结束语

