采用分量均值正交分割法设计矢量量化初始码书

邓宏贵，郭晟伟

(中南大学 物理科学与技术学院，湖南 长沙，410083)

矢量量化(Vector quantization, VQ)[1]技术是一种高效的数据压缩技术，由于其可以获得比标量量化更高的压缩比，故广泛应用于语音、图像和视频压缩系统。码书设计是矢量量化最关键的技术，直接影响到量化系统的性能。Linde等[2]提出的LBG算法物理含义清晰，数学推理严密，易于实现。但是，LBG算法严重依赖初始码书的选择，直接影响训练算法的收敛速度和码书质量。目前，初始码书有3种生成方法，即随机法、分裂法(Splitting algorithm, SA)[3-5]和乘积码书法。随机法就是从N个训练矢量中随机抽取M个作为初始码书。这种方法简单易行，且不会出现空胞腔，但结果具有较大偶然性。分裂法是首先把整个训练样本看成1个胞腔，再用最优分割超平面将胞腔一分为二，二分为四，直到形成M个胞腔，以这些胞腔的质心得到M个码字。采用该法量化失真小，但是，多维最优分割超平面的选择是一个非常复杂的问题[6]。乘积码书法以若干低维的码书作为乘积码，再求得高维码书，计算量小，但性能差。不同的初始码书会使LBG迭代算法陷入不同的局部最优解。目前，虽然人们对全局最优解进行了研究[7-9]，但计算量均很大。事实上，使初始码字根据样本分布规律尽量散开可以得到更好的迭代解[10-11]。在此，本文作者利用矢量在各个维度上的分量均值这一统计特性，将码书尽量散开得到充分利用，以便得到比以往算法更优的码书。

1 传统LBG算法

将N个输入矢量用M个码字矢量来量化，实际上是一个聚类问题，目前，没有多项式法求全局最优码书(均方量化误差最小的码书)。经典的LBG算法是基于最佳划分和最佳码字[12]这2个必要条件提出来的，采用迭代方法求得局部最优解。其算法步骤如下。

步骤 1：初始化，给定训练矢量集 T={xi|xi∈Rk,1≤i≤N}，码书大小为M，迭代门限ε＞0，初始码书为C(0)，置迭代次数t=0，初始失真D(-1)=∞。

步骤 2：依据最近邻法则[13]将 T划分为 M 个Voronoi胞腔。步骤 3：计算平均量化失真若失真下降率为(D(t-1)-D(t))/D(t)≤ε，则停止算法，码书C(t)就是所求的码书，否则转下一步。

步骤4：将M个胞腔的质心作为新码书，t=t+1，返回步骤2。

从以上步骤可以看出：LBG算法初始码书的选择至关重要，它影响到算法的收敛速度和最终码书的性能。传统初始码书生成方法一般采用随机法和分裂法，其中：随机法性能差，分裂法计算量大且性能有待提高[5]。本文从分量均值这一特征值出发，提出一种新的初始码书生成算法即分量均值正交分割法(Component mean orthogonal segmentation algorithm, CMOSA)。

2 分量均值正交分割法

2.1 基本思想

先引出2个与本文算法密切相关的概念——矢量均值和分量均值。

设x为Rk空间的k维矢量，xj(1≤j≤k)表示x在第j个维度的投影，矢量x的均值μx定义为：

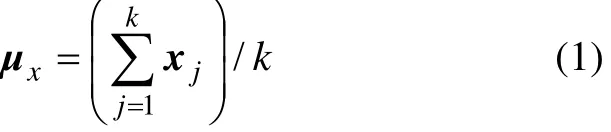
本文将其简记为矢量均值。

设xi(1≤i≤N)为Rk空间N个k维矢量，这N个矢量组成1个矢量组，xij(1≤i≤N, 1≤j≤k)表示矢量xi在第j个维度的投影。矢量组第j维分量的均值定义为：

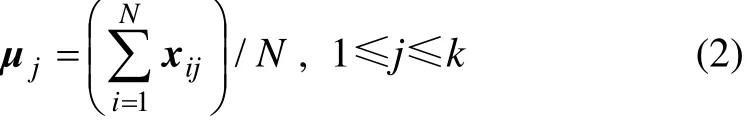
本文简记为分量均值。

引入如下定义：设L为Rk空间的1条直线，若L上任意点p=(p1, p2, …, pk)都满足p1=p2=…= pk，则称L为Rk的中心线[14]。

从物理意义上看，矢量x的矢量均值相当于矢量x在冗余维度xL=(x1+x1+…+xk)/k上的投影。x∀∈Rk，x 在 L 上的投影点为 px=(μx, μx, …, μx)。因此，与 L 正交的超平面上的所有点矢量均值相等，称为等均值超平面。

码书通常是以矢量均值划分样本空间，这样会出现1个问题：即使划分非常细，胞腔空间也是由2个无限宽的平行等均值超平面包裹，仍然存在欧式距离很大的码字同属一个胞腔的问题，而且矢量均值计算量大。该矢量均值仅仅是xL维度上的投影所致。这种方法只利用了训练样本在xL维度上的分布特点，而没有利用在其他维度上的分布特点，因而，不如直接依次用各分量空间的均值分割。这种在各个维度上都对训练样本空间进行分割的方法，使分割平面相互正交，由于每次分割只涉及1个相异的独立维度，计算量小，且同一胞腔内码字之间欧式距离小。根据这种情况，本文提出了基于分量均值分割的初始码书设计新算法。

2.2 实现步骤

假设有N个k维训练样本，码书大小为M，本文算法先计算N个训练样本在x1维度的均值μ1，利用该均值将样本空间一分为二，再将失真大的区域在 x2维度作正交分割共得到3个区域，依此类推，最终得到M个区域。以这些区域的质心作为初始码书，可以保证码字尽量散开，得到充分利用。新算法的实现步骤如下。

步骤 1：初始化。给定训练矢量集 T={xi|xi∈Rk,1≤i≤N}，最终码书大小为M，开始时所有训练矢量组成一个区域S1，置初始维度j=1，初始码字个数m=1，初始最大失真区域序号v=1。

步骤 2：按照式(2)计算最大失真区域 Sv在维度 j上的分量均值μj。使用μj将区域Sv一分为二，即Sm+1和 Sm+2。

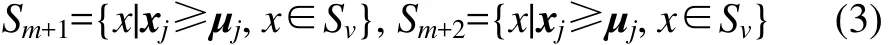
去掉Sv，以Sm+2代替Sv，保证区域个数增加1。若j=k，则j=1，否则j=j+1，m=m+1；若m=M，则结束分割，转步骤4。

步骤3：分别计算m个区域的平均量化失真Dt，找出失真最大的区域，即

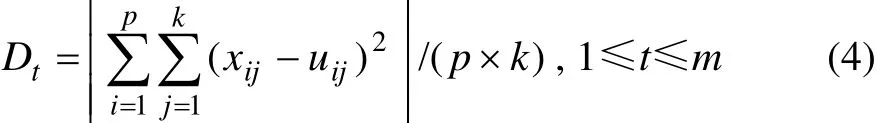
式中：p为区域St内样本个数。找出其中平均量化失真最大的区域序号v

步骤4：分别计算M个区域的质心，作为初始码书赋给LBG算法进行迭代。

该算法利用分量均值正交分割平均失真最大的区域，直至形成需要的M个初始胞腔，以分割后的区域质心作为初始码书放到 LBG算法迭代。需要说明的是：按照这些步骤获得的初始码书不是最优码书。本方法的目的只是为 LBG算法提供大致按照训练样本规律分布的初始码字，使初始码字得到充分利用。

2.3 非均匀分布样本改进措施

从上述基本思想和实现步骤可以看出：分量均值正交分割设计法对于均匀分布的样本特别有效。实际上，大多数图像样本都不是完全地均匀分布，这样，对某一区域分割时，若少数几个样本在维度xj上与其他样本差别很大，则可能出现非典型码字(映射到该码字的样本数目很少)，这些码字利用率不高。由于该算法以分量均值分割，每个新区域至少包含1个样本，因此，不可能出现空胞腔，至多出现非典型码字。为了解决该算法的非典型码字问题，需要对步骤2略加改进，具体方法如下。

对于分割得到的2个新胞腔，统计其中样本数pi(i为m+1和m+2)。若pi小于预先设定的非典型码字门限Ns，则认定该码字为非典型码字，去掉区域Si，将其中样本划分给其他最临近的码字所属胞腔。这样，本次操作相当于只对离中心码字较远的部分样本进行调整，而不增加胞腔个数。参数Ns一般是训练样本规模N的弱函数，Ns随着N增大而略增大，经验值取3～5为宜。

经过改进之后，本文的分量均值正交分割法对于非均匀分布样本同样适用，应用范围扩大。

3 算法仿真及结果讨论

实验硬件环境：CPU(P4 2.93 G)，内存为512 M，DDR；实验软件环境：Visual C++ 6.0。

从标准测试图像库中选取10幅大小为256×256和256色的灰度图像进行测试。将图像划为4×4的小块，因此，矢量维数k=16，样本数N=4 096，码书大小 M∈{8，16，32，64，128，256，512，1 024}，失真下降门限ε取0.001。分别用LBG算法[2]、SA+LBG算法[15]、本文算法进行码书设计，把各种方法在不同码书下的失真度和训练时间这2个最重要的参数进行对比。其中，训练时间包括初始码书设计时间和迭代优化时间，失真度用峰值信噪比RPSN度量。

设原始像素为xij，量化值为qij，均方误差EMS、峰值信噪比RPSN定义为：

选取最典型的Lena和Barb 2幅图像，在码书大小为128时进行对比，结果见表1。图1所示为3种算法在不同码书大小下失真度的对比结果；图2所示为不同码书大小下训练时间对比结果。实验结果表明：本文提出的分量均值正交分割法与经典 LBG算法相比，峰值信噪比RPSN提高超过1 dB，训练时间增加不超过30%；相对于SA+LBG法，RPSN相差不超过0.1 dB，但训练速度提高了 1.0～1.5倍。其原因是：以随机方式产生初始码书的LBG算法，不需要附加计算，耗时最少。但是，由于初始码字不能自适应于训练样本的统计特性，最终收敛到RPSN较低的局部最优解。用SA产生初始码书，可以使初始胞腔沿着失真下降最大的方向分裂，产生较好码书，但是，在分裂过程中，寻找最优分割超平面需进行繁琐的运算，算法应用受到限制。本文提出的CMOSA算法，充分利用了正交分割平均失真最大的胞腔，使初始码字尽量散开，再在LBG算法中迭代，最终码书质量比随机LBG的质量高得多，与SA和LBG联合算法相比码书质量相差很小。由于CMOSA算法只需M次分量均值的计算，相对于分裂法M次分裂[6]少得多，故比SA和LBG联合算法的运算速率快得多。

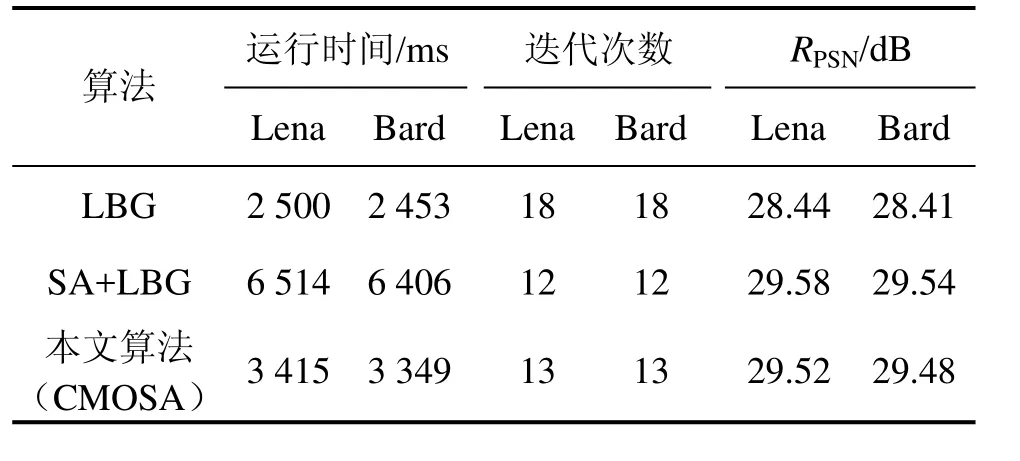
表1 Lena和Barb图像在3种算法下的性能对比(M=128)Table 1 Performance comparison of three algorithms for Lena and Barb images (M=128)

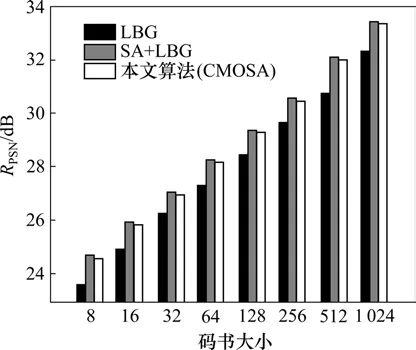
图1 3种算法的RPSN对比Fig.1 Comparison of peak signal to noise ratio of three algorithms

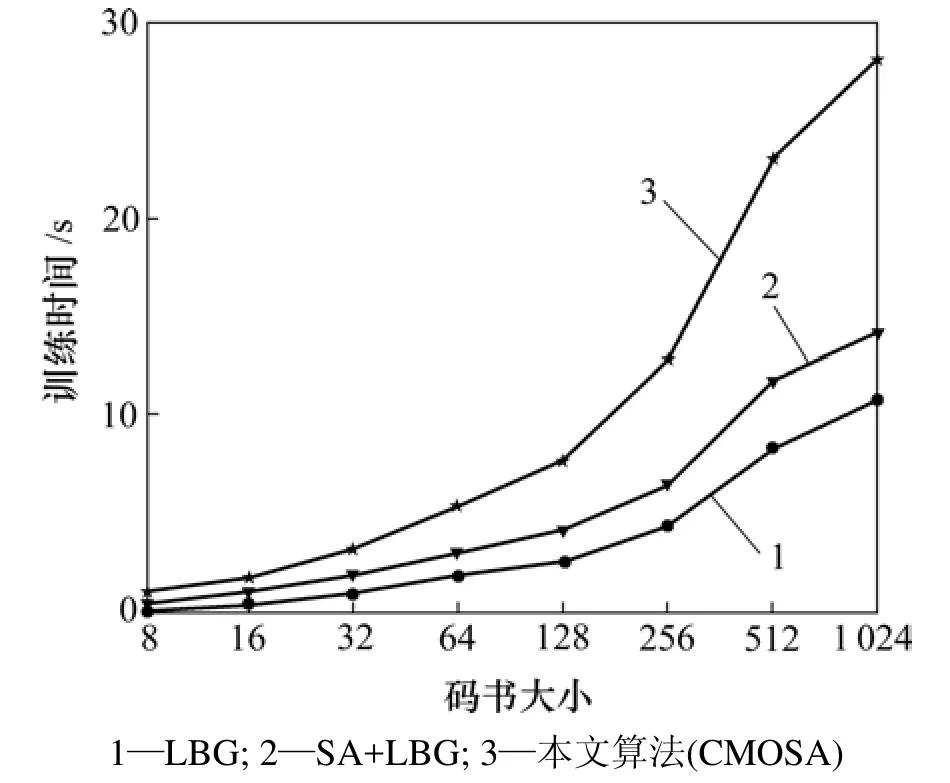
图2 3种算法训练时间对比Fig.2 Training time comparison of three algorithms

4 结论

(1) 基于分量均值正交分割平均失真最大的胞腔，提出了一种矢量量化初始码书设计算法即CMOSA算法。

(2) CMOSA算法量化误差小。与经典LBG算法相比，CMOSA算法峰值信噪比提高超过1 dB；与SA和LBG联合算法相比，峰值信噪比相差低于0.1 dB。

(3) CMOSA算法运算量小。CMOSA算法与经典LBG算法相比，训练时间增加不超过30%；与SA和

LBG联合算法相比，训练速度提高1.0～1.5倍。

[1] Gersho A, Gray R M. Vector quantization and signal compression[M]. Boston: Kluwer Academic Publishers, 1992.

[2] Linde Y, Buzo A, Gray R M. An algorithm for vector quantizer design[J]. IEEE Transactions on Communications, 1980, 28(1):84-95.

[3] Lee W F, Chan C K. Two-dimensional split and merge algorithm for differential vector quantization of images[J]. Image Communication, 1998, 13(1): 1-14.

[4] Stephen S, Kuldip K P. Efficient product code vector quantisation using the switched split vector quantiser[J]. Digital Signal Processing, 2007, 17(1): 138-171.

[5] Ahmed M E. Fast methods for split codebooks[J]. Signal Processing, 2000, 80(12): 2553-2565.

[6] Chan C K, Ma C K. A fast method of designing better codebooks for image vector quantization[J]. IEEE Transactions on Communications, 1994, 42(234): 237-242.

[7] Franti P. Genetic algorithm with deterministic crossover for vector quantization[J]. Pattern Recognition Letters, 2000, 21:61-68.

[8] 李霞, 罗雪晖, 张基宏. 基于人工蚁群优化的矢量量化码书设计算法[J]. 电子学报, 2004, 32(7): 1082-1085.LI Xia, LUO Xue-hui, ZHANG Ji-hong. Codebook design for image vector quantization with ant colony optimization[J]. Acta Electronica Sinica, 2004, 32(7): 1082-1085.

[9] 陆哲明, 潘正祥, 孙圣和. 基于改进禁止搜索算法的矢量量化码书设计[J]. 电子学报, 2000, 28(9): 108-110.LU Zhe-ming, PAN Zheng-xiang, SUN Sheng-he. VQ codebook design based on the modified tabu search algorithms[J]. Acta Electronica Sinica, 2000, 28(9): 108-110.

[10] Villmann T, Schleif F, Hammer B. Comparison of relevance learning vector quantization with other metric adaptive classification methods[J]. Neural Networks, 2006, 19(5):610-622.

[11] Shen F, Hasegawa O. An adaptive incremental LBG for vector quantization[J]. Neural Networks, 2006, 19(5): 694-704.

[12] Lloyd S. Least squares quantization in PCM[J]. IEEE Transactions on Information Theory, 1982, 28(2): 129-137.

[13] Garey M R, Johnson D S, Witsenhausen H S. The complexity of the generalized Loyd-Max problem[J]. IEEE Transactions on Information Theory, 1982, 28(2): 255-256.

[14] Ra S W, Kim J K. Fast mean-distance-ordered partial codebook search algorithm for image vector quantization[J]. IEEE Transactions on Circuits and Systems-II, 1993, 40(9): 576-579.

[15] 李弼程, 文超, 平西建. 两个优于分裂法的初始码书设计算法[J]. 中国图像图形学报, 2000, 5(1): 48-51.LI Bi-cheng, WEN Chao, PING Xi-jian. On the design of original codebooks with two algorithms better than the splitting algorithm[J]. Journal of Image and Graphics, 2000, 5(1): 48-51.