基于节理几何参数不确定性的边坡可靠度分析

许湘华 ，曲广琇，方理刚

(1. 中南大学 土木建筑学院，湖南 长沙，410075；2. 贵州省交通规划勘察设计研究院，贵州 贵阳，550001)

在很多情况下，岩体受规模不同、方向各异的多组节理的切割，破坏了岩体的连续性和完整性，导致岩体强度和变形性质的各向异性，更使得岩质边坡系统具有高度不确定性。节理化岩质边坡系统的不确定性归根结底来源于节理面的随机分布。对节理参数的不确定性进行研究和对基于节理参数不确定性的岩质边坡可靠度进行分析，在岩质边坡可靠性评价中显得尤为重要。节理几何参数的概率分布模型主要有均匀分布、负指数分布、正态分布、对数正态分布等[1-6]。为了分析节理参数的不确定性对岩质边坡可靠性的影响，近年来，可靠度理论被引入边坡可靠性评价中，如：何满潮等[7-8]将结构面的力学参数作为随机变量，几何参数作为确定值；张奇华[9]把滑面倾角和力学参数作为随机变量，将坡体体积、滑面面积和其他结构面倾角等随机量看作确定值，对边坡可靠度进行分析，但还存在不足；孙树林等[10]综合考虑块体结构面几何形状和力学参数的不确定性，把随机概率模型引入块体理论，分析了不同结构面参数下边坡的可靠度；赵奎等[11]探讨了节理面构成块体的概率公式并对其进行工程应用，分析了边坡的可靠度。这些研究成果对于由构造控制的边坡可靠度分析具有重要意义，但是，因节理参数存在不确定性，研究者对岩质边坡的可靠性评价不尽合理，同时，考虑节理参数不确定性的边坡可靠度分析理论也尚未建立；因此，考虑节理参数随机变化对岩质边坡可靠性影响的分析仍倍受关注，仍需对基于节理参数不确定性的边坡可靠度进行分析。在此，本文作者通过理论研究确定节理几何参数的概率分布类型，分析其不确定性。以节理倾向、倾角和间距为随机变量，提出基于节理几何参数不确定性的边坡可靠度分析方法，并对实际问题进行可靠度分析，以便为岩质边坡的可靠性评价和防护设计提供理论依据和参考。

1 节理几何参数不确定性分析

1.1 节理几何参数调查与统计

为了给节理几何参数的不确定性分析提供数据，采用测线法对厦蓉(厦门—成都)高速公路某路堑边坡进行现场节理调查以获取大量的节理样本。根据结构面控制理论，优势节理控制着边坡的稳定性，为此，在进行节理几何参数概率分布类型分析之前，应用赤平极射投影法对测量的节理样本优势节理进行分组。边坡体内主要发育4组优势节理组，其优势产状分别为：150°∠82°，200°∠69°，240°∠80°和 300°∠10°。针对以上节理分组，通过数理统计理论分别对每组节理的倾向α、倾角β和间距χ进行统计分析，得到相应的概率统计参数，如表1所示。

1.2 节理几何参数概率分布类型确定

1.2.1 概率图法基本原理

对某一组节理参数n个数据x1, x2, …, xn，选用某一概率分布函数F(x)。首先，将x1, x2, …, xn按其顺序排队，为 θ1, θ2, …, θn。这样，从理论上讲，相应 θi的分布函数应为 F(θi)=i/n。为了避免出现在 i=n时F(θn)=1的不合理现象，定义经验分布函数值为：

选定F(x)为其理论分布函数，则

以θi为横坐标，θt为纵坐标，可以将n个数据点绘在该坐标系中。理论上，该n个点应连成1条与横轴呈夹角为 45°且通过原点的直线。在实际应用中，若该n个点大致上沿1条直线分布，则不论截距和斜率多大，都可以认为该组数据符合所选用的概型F(x)。

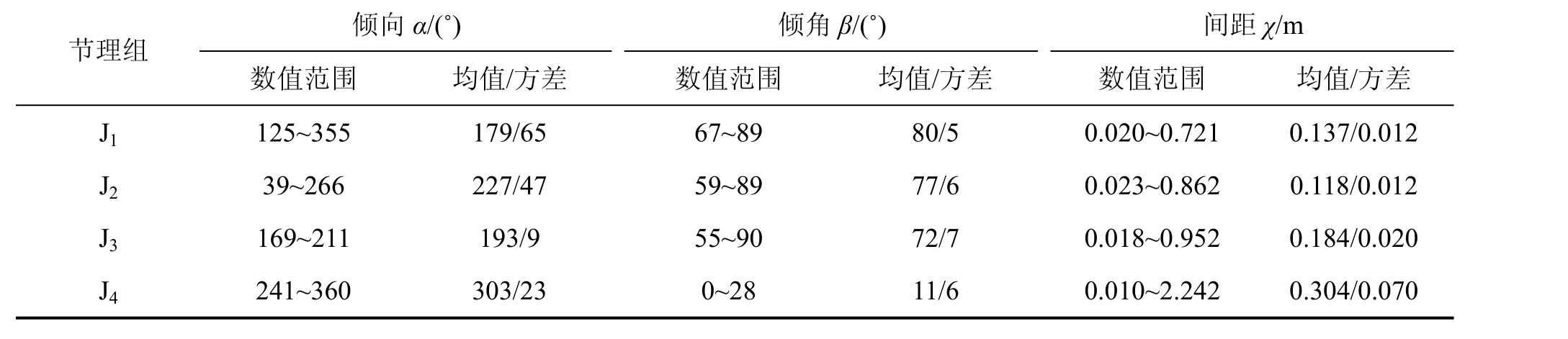
表1 节理几何参数(α，β，χ)的概率统计参数Table1 Probability statistical parameters of joint geometric parameters (α, β, χ)

1.2.2 结果分析

为了分析节理几何参数的不确定性，采用概率图法研究各组节理倾向、倾角和间距的概率分布类型，以确定其概率密度，分析结果见图2～9。

图 1所示为 J1组节理倾角正态分布模型的概率。从图1可以看出：曲线的数据点基本落在同一条直线上，并且该直线具有通过原点且倾角为 45°的特征。对于其他3种分布类型， J1组节理倾角符合正态分布。

通过数理统计理论，确定J1组节理倾角概率密度为：

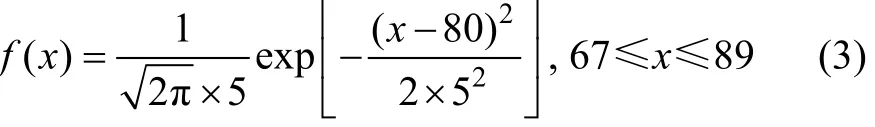
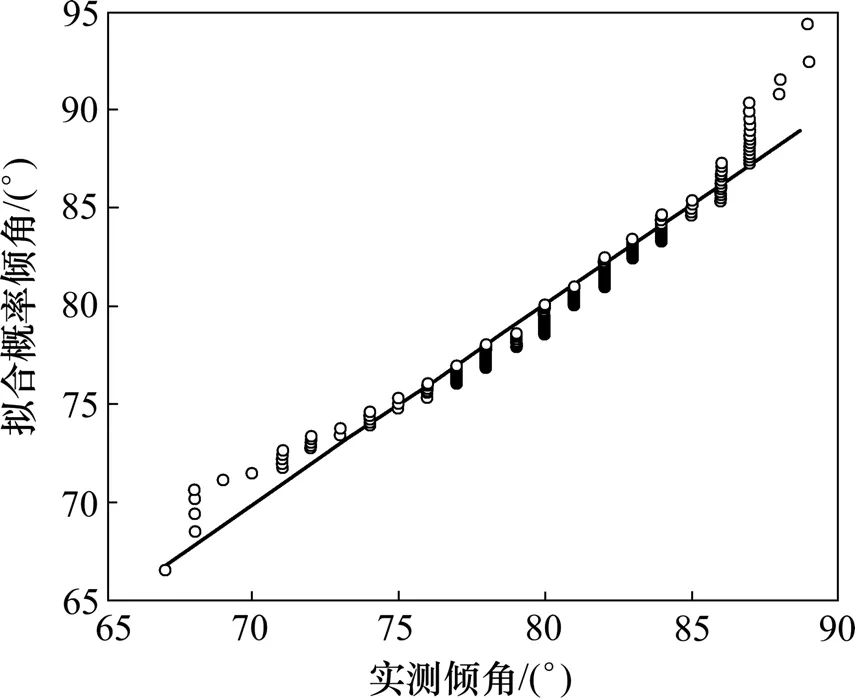
图1 J1节理倾角正态分布概率图Fig.1 Normal distribution probability diagram of J1 dip

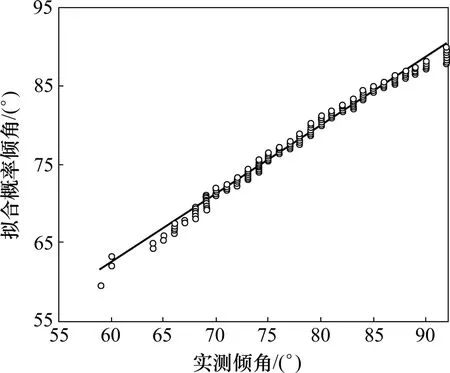
图2 J2节理倾角正态分布概率图Fig.2 Normal distribution probability diagram of J2 dip

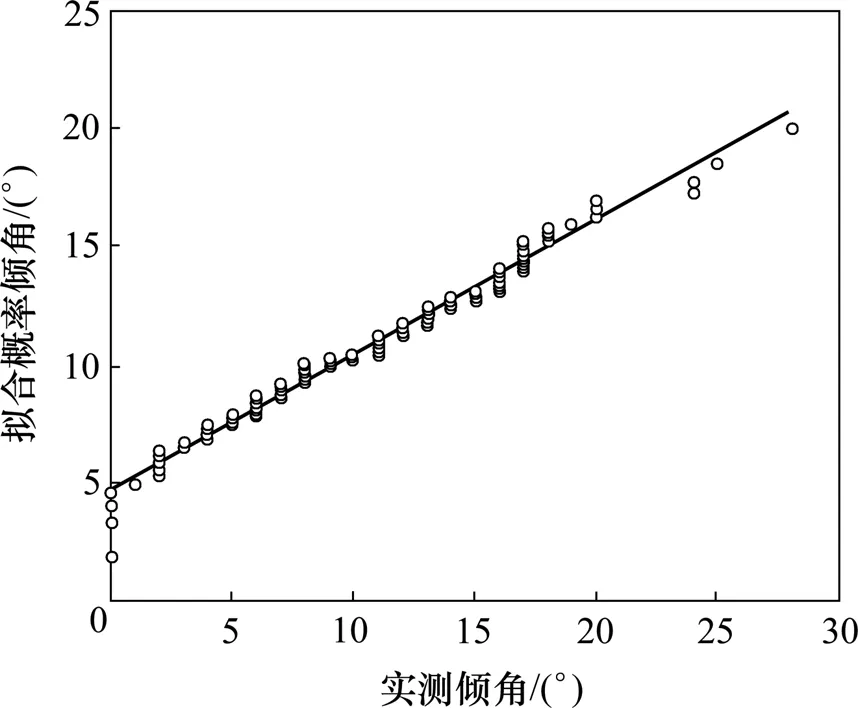
图3 J4节理倾角正态分布概率图Fig.3 Normal distribution probability diagram of J4 dip

图4 J1节理倾向对数正态分布概率图Fig.4 Lognormal distribution probability diagram of J1 joint trend

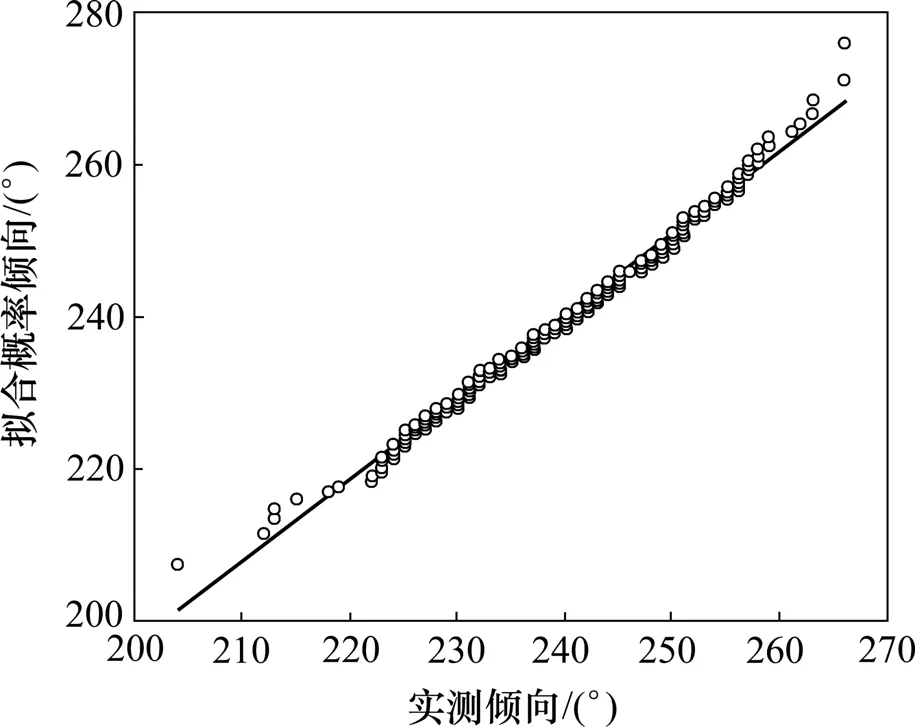
图5 J2节理倾向对数正态分布概率图Fig.5 Lognormal distribution probability diagram of J2 joint trend

图2 和图3所示分别为J2和J4节理倾角的分布概率。从图2和图3可以看出：在正态分布模型下，2组节理倾角基本连成1条倾斜角为45°的直线。图4～6所示为J1，J2和J4节理倾向的分布概率，它们的节理间距分布概率分别如图7～9所示。可以看出：在相应的分布模型下，分布曲线的变化趋势符合概率图法原理，能够体现其分布形式；此外，以上概率图中有部分离散点，这是由个别样本数据误差造成的，并不影响样本总体的分布形式。分析结果表明：各组节理的倾角多呈正态分布，节理倾向多呈对数正态分布，节理间距多呈负指数分布。结合数理统计理论，确定了研究区域内节理几何参数的不确定性及其分布概率密度。概率密度函数参数即分布特征参数如表2所示。

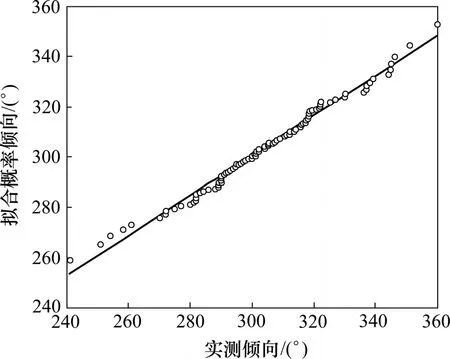
图6 J4节理倾向对数正态分布概率图Fig.6 Lognormal distribution probability diagram of J4 joint trend

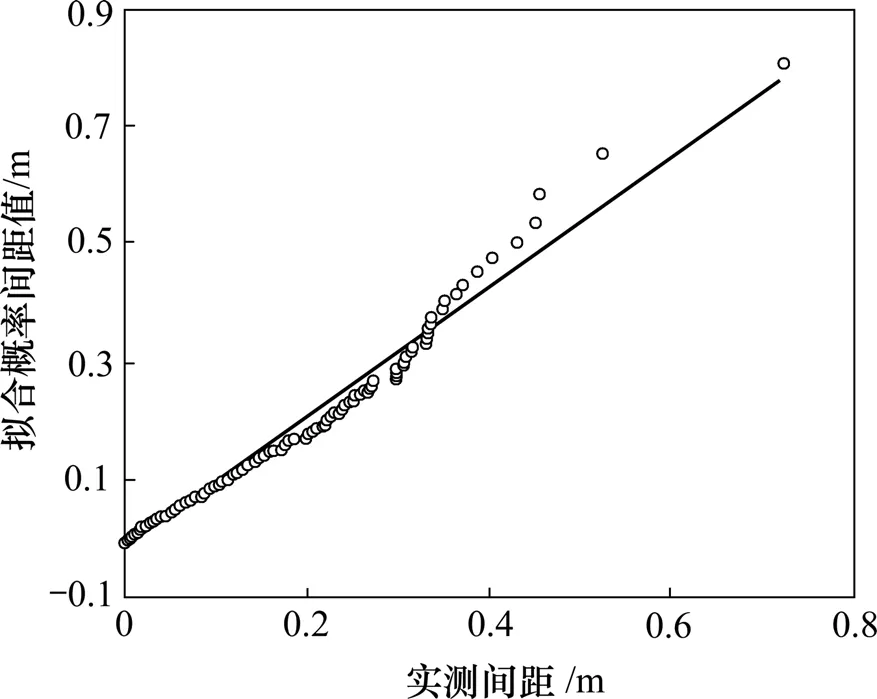
图7 J1节理间距负指数分布概率图Fig.7 Negative exponential distribution probability diagram of J1 joint spacing

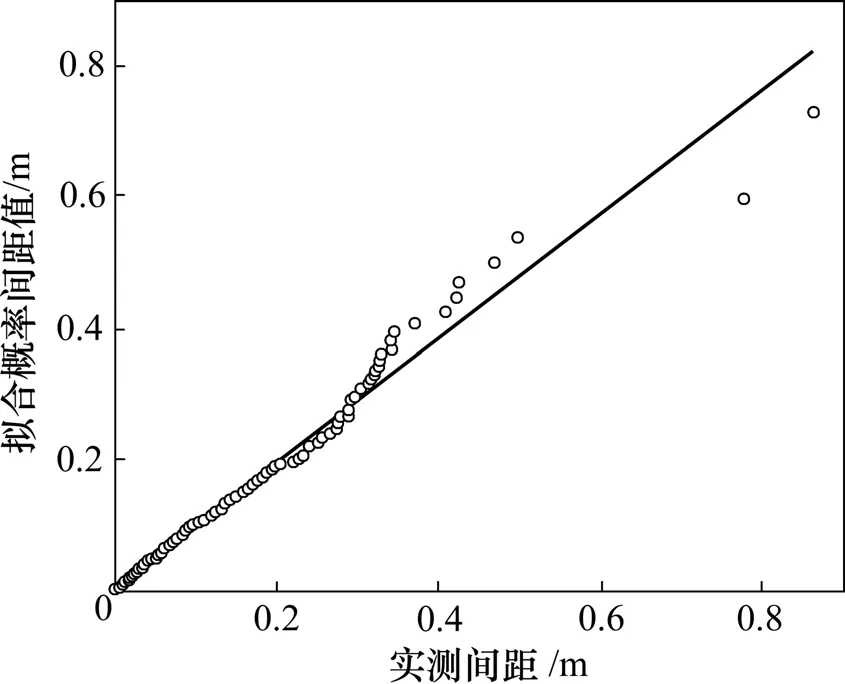
图8 J2节理间距负指数分布概率图Fig.8 Negative exponential distribution probability diagram of J2 joint spacing

图9 J4节理间距负指数分布概率图Fig.9 Negative exponential distribution probability diagram of J4 joint spacing

表2 边坡稳定性分析的物理力学参数Table 2 Physical and mechanical parameters for stability analysis of rock slope

2 考虑节理几何参数不确定性的边坡可靠性模型的建立与运算

为了建立考虑节理几何参数不确定性的边坡可靠性分析模型，基于现场勘测的双滑面(J2与 J3组合)边坡破坏模式，采用Sarma法对边坡安全系数进行计算。由于Sarma法安全系数计算格式为隐函数，极限状态方程无法建立，为此，根据响应面法理论，研究基于Sarma法的边坡极限状态方程 RSM(Response surface method)重构，提出基于节理几何参数不确定性的边坡可靠度分析方法。

2.1 RSM重构原理

对于n个随机变量x1, x2, …, xn，RSM解析表达式通常为：

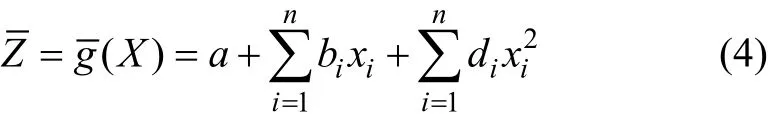
式中：a, bi和di(i=1, 2, …, n)均为待定系数，共2n+1个系数。

应用RSM方法重构1个解析表达式，按下述步骤进行：

(2) 根据抽样所得样本，利用安全系数K的迭代计算过程计算2n+1个函数值。

(3) 由于式(4)中只有2n+1个待定系数，利用上述迭代得到的 2n+1个函数值解出待定系数 a, bi和 di(i=1, 2, …, n)，得到二次多项式近似功能函数的解析表达式。

(4) 在得出工程近似状态函数后，可确定结构的极限状态重构方程为：

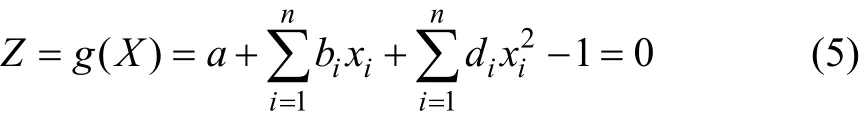
RSM 重构极限状态方程的计算结果精度满足工程要求[12-14]。

2.2 随机变量选取

以每个结构面即节理面的倾向(α1和 α2)、倾角(β1和 β2)、间距(x1和 x2)为随机变量，岩体重度 γ、边坡高度H，强度参数(C和φ)等作为常量，进行边坡可靠度分析。令 X1=α1，X2=α2，X3=β1，X4=β2，X5= x1，X6= x2，将随机变量表示为随机向量的形式X=( X1，X2，X3，X4，X5，X6)，其变量参数见表 3。

2.3 极限状态功能函数构建

Sarma法安全系数是一个隐函数，无法写出边坡稳定极限状态的解析方程。为了实现隐式功能函数的边坡可靠性评价，根据 RSM 重构原理，考虑本文选定的随机变量，确定边坡稳定极限状态功能函数为：

式(6)中有6个随机变量，共13个待定参数。为求解这13个待定系数，将RSM重构思路与Sarma迭代方法结合起来。抽取计算待定参数的样点值，如表4所示。

将样点值代入式(6)，联立方程求解待定参数，确定极限状态功能函数为：

至此，建立了基于节理几何参数不确定性的Sarma模式响应面法边坡可靠性分析模型，为进行岩质边坡可靠度分析奠定了基础。

2.4 可靠度计算

采用蒙特卡洛法产生随机数，利用构建的极限状态功能函数(式(7))进行边坡可靠度计算。已知边坡岩土体力学参数、几何参数等基本随机变量的概率分布时，根据边坡的极限状态函数Z=g(X1, X2, …, Xn)，利用蒙特卡洛方法产生符合基本随机变量概率分布的一组随机数 x1, x2, …, xn，代入极限状态函数 Z=g(X1,X2, …, Xn)，得出极限状态函数的1个随机数z1，用同样的方法产生 N个极限状态函数的随机数 z1, z2, …,zn。如果在N个极限状态函数的随机数中有M个小于1、等于1或小于等于0，当N足够大时，根据大数定理，此时的频率已近似于概率，因而，可得边坡的破坏概率或者可靠度。

表3 节理几何参数(α，β，χ)概率分布形式及其分布特征参数统计Table 3 Probability distribution form of joint geometric parameters (α, β, χ) and its distribution parameters

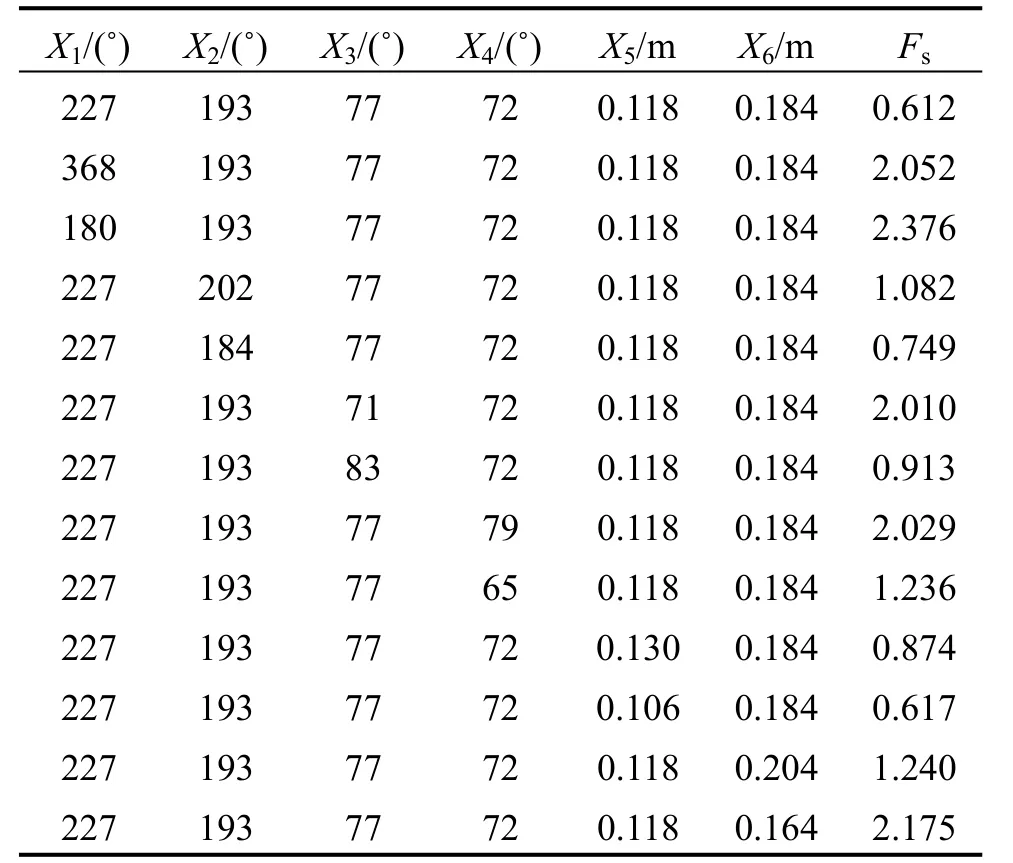
表4 确定极限状态功能函数系数的样点值Table 4 Sample values to determinate coefficients of limit state functional function

考虑采用蒙特卡罗法研究随机事件的破坏概率时对模拟次数的要求，根据本文研究方法确定模拟次数为10 000次，能够满足计算精确要求。基于节理几何参数的概率分布类型及其特征参数，由蒙特卡罗法产生10 000组符合随机变量分布类型的随机数Xi，根据所建立的计算模型获得稳定安全系数Zi数组，同时得到Z的统计特征及其小于0的次数m、边坡的破坏概率pf及可靠度指标β。

式中：N为模拟次数；m为破坏次数；µz和σz分别为Z的均值和方差。

3 边坡可靠性评价

根据上述分析模型和运算过程，经计算，实例边坡的破坏概率为25.64，可靠度指标为1.93，平均稳定安全系数为1.21。边坡稳定安全系数的统计直方图如图10所示。

图10 安全系数(Fs)统计直方图Fig.10 Histogram of factor of safety (Fs)

从图10可以看出：有部分安全系数小于0，这说明实际边坡工程存在一定的破坏风险。计算结果表明：边坡处于非稳定状态，而其平均稳定安全系数大于1，说明边坡工程稳定、可靠。这与实例边坡破坏概率较大的事实不符，验证了进行边坡可靠度分析的必要性。

为了研究节理几何参数不确定性对边坡可靠性的影响，在相同模拟次数下计算不同节理几何参数下的边坡破坏概率，如图11所示。

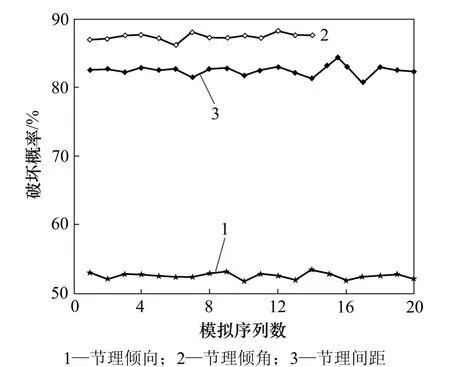
图11 节理几何参数不确定性对边坡稳定性的影响Fig.11 Effects of uncertainty in joint geometric parameters on stability of rock slope

从图11可以看出：节理倾向、倾角和间距对边坡破坏概率的贡献是不同的；节理倾角对边坡破坏概率的贡献最大，破坏概率达到87%左右；节理倾向对边坡破坏概率的贡献最小，其破坏概率为52%左右。这说明节理间距和节理倾角的随机分布，严重切割了岩体的完整性，导致岩体力学强度下降，边坡的稳定性降低。节理倾向的随机分布对岩体的破坏作用较低，但对边坡稳定性也有一定程度的影响。研究结果表明：基于构造控制的岩质边坡、节理倾角和间距对边坡可靠性有非常明显的影响，是影响边坡稳定的主导因素。因此，在岩质边坡地质勘测中要尽可能获得断层、节理等详细资料，从而提高边坡可靠度分析结果的准确性；此外，针对节理倾角的主导影响，可以通过设计合适的锚固角来施加锚固力，从而提高边坡的可靠性。

4 结论

(1) 在优势节理分组的基础上，通过数理统计与概率图法分析了每组节理几何参数的概率分布类型，得出各组节理倾角多呈正态分布，节理倾向多呈对数正态分布，节理间距多呈负指数分布，确定了研究区域内节理几何参数的不确定性及其分布概率密度。同时，验证了数理统计与概率图法相结合的方法是确定节理几何参数不确定性的一种有效方法。

(2) 建立了考虑节理几何参数不确定性的 Sarma模式响应面边坡可靠性分析模型，提出了基于节理几何参数不确定性的边坡可靠度分析方法，分析了实例边坡的可靠性。本文提出的可靠度分析方法能用于准确地评价岩质边坡工程的可靠性，是一种行之有效的可靠度分析方法。

(3) 节理倾向、节理倾角和节理间距是影响边坡稳定性的主导因素，因此，在进行边坡稳定性分析时要尽可能地详细调查节理等结构面资料，在边坡防护设计时设计合适的锚固角等，从而实现岩质边坡开挖和支护方案的优化设计。

[1] 徐光黎, 潘别桐, 唐辉明, 等. 岩体结构模型与应用[M]. 北京: 中国地质大学出版社, 1993.XU Guang-li, PAN Bie-tong, TANG Hui-ming, et al. Structure model and application of rock mass[M]. Beijing: China University of Geosciences Press,1993.

[2] 陈祖煜, 汪小刚, 杨建, 等. 岩质边坡稳定性分析—原理·方法·程序[M]. 北京: 中国水利水电出版社, 2005.CHEN Zu-yu, WANG Xiao-gang, YANG Jian, et al. Rock slope stability analysis—Principles · methods · program[M]. Beijing:China Water Conservancy and Hydropower Press, 2005.

[3] Goodman R E, Taylor R L, Brekke T L. A model for the mechanics of jointed rock[J]. Journal of the Soil Mechanics and Foundations, 1968, 194(3): 637-659.

[4] Hudson J A, Priest S D. Discontinuities frequency in rock masses[J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1983, 20(2): 73-89.

[5] Kulatilake P H S W, Wu T H. The density of discontinuity traces in sampling windows[J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts,1984, 21(6): 181-190.

[6] Priest S D, Hudson J A. Estimation of discontinuity spacing and trace length using scanline surveys[J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1981, 18(3): 183-197.

[7] 何满潮, 苏永华, 景海河. 块状岩体的稳定可靠性分析模型及其应用[J]. 岩石力学与工程学报, 2002, 21(3): 343-345.HE Man-chao, SU Yong-hua, JING Hai-he. Reliability analysis model of block rock mass stability and its application[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(3):343-345.

[8] 苏永华, 姚爱军, 刘晓明. 裂隙化硬岩洞室围岩失稳分析方法[J]. 岩土力学, 2004, 25(7): 1085-1088.SU Yong-hua, YAO Ai-jun, LIU Xiao-ming. Probability analysis of stability underground cave surrounding rock in fissured rock mass[J]. Rock and Soil Mechanics, 2004, 25(7): 1085-1088.

[9] 张奇华. 块体理论的应用基础研究与软件开发[D]. 武汉: 武汉大学土木建筑学院, 2004: 10-20.ZHANG Qi-hua. Basic study on application of block theory and development of analytical software[D]. Wuhan: Wuhan University. School of Civil Engineering and Architecture, 2004:10-20.

[10] 孙树林, 朱杰. 节理化岩质边坡的关键块体可靠度分析[J].岩石力学与工程学报, 2007, 26(1): 131-136.SUN Shu-lin, ZHU Jie. Reliability analysis of key block for a jointed rock slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(1): 131-136.

[11] 赵奎, 王晓军, 赵康, 等. 节理面构成块体的概率公式及其工程应用[J]. 岩土力学, 2006, 27(3): 369-372.ZHAO Kui, WANG Xiao-jun, ZHAO Kang, et al. A new probability formula of blocks cut by joint planes and its engineering application[J]. Rock and Soil Mechanics, 2006,27(3): 369-372.

[12] 苏永华, 赵明华, 邹志鹏, 等. 边坡稳定性分析的Sarma模式及其可靠度计算方法[J]. 水利学报, 2006, 37(4): 457-463.SU Yong-hua, ZHAO Ming-hua, ZOU Zhi-peng, et al. Sarma model for slope stability analysis and its reliability degree calculation method[J]. Shuili Xuebao, 2006, 37(4): 457-463.

[13] 谭晓慧, 王建国, 刘新荣. 改进的响应面法及其在可靠度分析中的应用[J]. 岩石力学与工程学报, 2005, 24(S2):5874-5879.TAN Xiao-hui, WANG Jian-guo, LIU Xin-rong. Improved response surface method and its application to reliability analysis[J]. Chinese Journal of Rock Mechanics and Engineering,2005, 24(S2): 5874-5879.

[14] 苏永华, 赵明华, 蒋德松, 等. 响应面方法在边坡稳定可靠度分析中的应用[J]. 岩石力学与工程学报, 2006, 25(7):1417-1424.SU Yong-hua, ZHAO Ming-hua, JIANG De-song. Application of response surface method to reliability analysis of slope stability[J]. Chinese Journal of Rock Mechanics and Engineering,2006, 25(7): 1417-1424.