双圆弧数值算法在NURBS曲线插补中的应用
史旭光 胥布工
华南理工大学,广州,510640
0 引言
随着硬件平台的不断改善以及曲线曲面造型理论的发展,CNC系统处理参数样条曲线的能力受到研究者的重视。国外著名厂商如日本FANUC公司已将非均匀有理B样条(NURBS)插补功能集成于其产品中,日本Mitsubishi、德国SIEMENS已经开发出了带此项功能的CNC系统。Piegl等[1]解释了NURBS应用的一些理论性问题,为NURBS技术发展和应用奠定了基础。此后,相关研究论文不断涌现:Yang等[2]最早利用一阶和二阶泰勒展开计算参数曲线进给量,Yeh等[3]给出了依据曲线曲率来动态改变速度进给的理论依据;彭芳瑜等[4]将速度前瞻控制技术引入参数曲线插补理论中,Guo等[5]研究了机床动力学特性及自适应插补策略,李建刚等[6]提出了在线速度修正的NURBS曲线插补器结构,赵国勇等[7]研究了加速度和弓高误差约束条件下的NURBS曲线插补问题。
针对NURBS曲线、曲面在数控领域中的应用,相关研究包括如何减少数值计算复杂度、结合反馈控制策略提高加工精度、结合机械动力学约束条件提高运动平滑度等,这些工作在上述文献中已得到较为充分的挖掘,而对于NURBS曲线这一类较特殊的曲线在CNC系统内部采用何种方式去逼近以获得较为满意的控制效果,相关文献论述不多。另外,由于参数样条曲线本身构造的局限性,即其数值计算存在截断误差,这一特性直接导致其切线方向计算的不稳定性,由此带来了速度波动性问题,相关学者提出了具有数值反馈特性的自适应插补概念[8],本文将对这一问题进行探讨并展开实验研究。
1 NURBS曲线应用数学理论基础
依据文献[1],一条k次NURBS曲线可表示为一分段有理多项式函数:
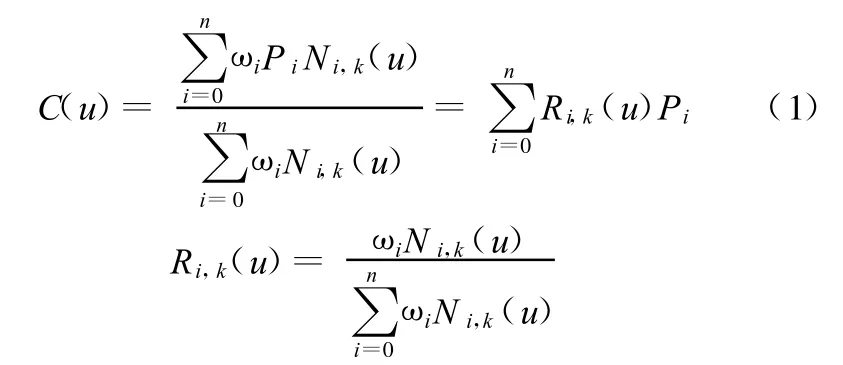
式中,u为参变量,u∈[0,1];Ri,k(u)为该NURBS曲线的有理基底函数;Pi为控制点;ωi为控制点Pi的权因子;Ni,k(u)为k次规范B样条基函数。
NURBS曲线插补需要计算相应参数曲线导数,如 C(1)(u)、C(2)(u)等,需要对每个控制节点的基底函数Ri,k(u)进行求导,相应一阶、二阶求导公式如下:

由式(2)、式(3)知,进行NURBS曲线计算需要进行大量数据运算工作,其算法效率极大影响着CNC系统工作的有效性。
2 双圆弧算法
对现代CNC系统配备高次曲线插补功能是目前的研究热点,各种曲线计算方法层出不穷,其中双圆弧形式数值计算方法开始进入相关研究人员的视野。Piegl等[9]给出了双圆弧(biarc)应用于曲线逼近的若干重要特征。以此为理论基础,本文给出其具体分析过程。
双圆弧由两个光滑连接的圆弧构成,用来逼近已知起点和终点的曲线段。具体描述如下:给定某曲线段的起点P s和终点P e,并且相应知道起点和终点单位切向量Ts和Te,则双圆弧逼近问题需要满足以下三条规律:①该双圆弧通过该段曲线起点Ps和终点Pe;②在起点Ps具有和该曲线相同的切向量T s,终点处具有相同的切向量T e;③构成双圆弧的两个子圆弧以G1型光滑连接。
由于双圆弧具有以上特点,因而具备描述曲线段一阶切向量的性质,相对于传统上的直线段和单圆弧法能够容纳被描述曲线段的更多物理信息。应用此理论于数控系统加工中,可以获得更为平坦而光滑的加工轨迹,理论上可以保证轨迹曲线段斜率连续,也可以用较少的圆弧来逼近原先设计的曲线,减轻了数据传输负担。
根据Piegl等的定义给出双圆弧应用曲线逼近一般理论推导过程:一个双圆弧完整的约束条件只需要相应的5个控制点即可,如图1中的P s、P1 、P2 、P3 、P e 。

图1 双圆弧曲线逼近示意图
不失一般性,我们由相应的定义可以给出未知的三个控制点计算公式:

式中,α和β均为正数。
取中间变量v=P s-P e,整理式(6)可得
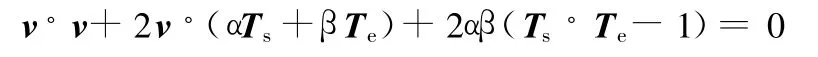
上式中未知变量为α、β,令r=α/β,则有
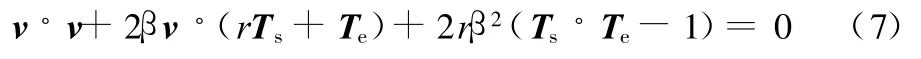
相当多的研究文献集中于r值的分析,我们取r=1,大大简化了数值计算工作量,其相应的曲线描述效果也经过了实验检测。为将上述双圆弧曲线逼近理论应用于NURBS插补过程中,这里给出具体实现算法步骤。
NURBS参数曲线插补问题一般可表述为如下形式:
假设某一个三维空间曲线可表示为

设当前曲线路径坐标为
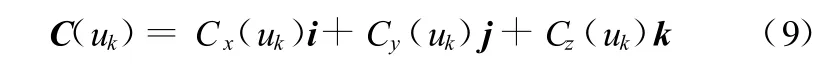
则下一个插补周期相应轨迹坐标为
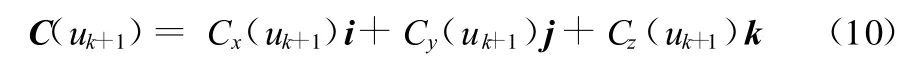
通过不断地进行uk+1=uk+Δu的迭代运算,从而获得完整的曲线路径坐标。获得了曲线路径坐标只是完成了插补工作的第一部分即粗插补部分,接下来利用双圆弧实现对前一段粗插即C(uk)和C(uk+1)之间数据的密化,亦即完成精插补。利用双圆弧实现精插的基本原理是:利用已知的计算得到的 NURBS曲线上的点C(uk)和C(uk+1)作为双圆弧的起始坐标和终点坐标,即为式(4)、式(5)中的P s和P e,而利用式(7)获得关键中间点P2,则曲线分布构成为P s P2和P2P e两部分曲线,相应地用两段圆弧去逼近原始曲线,这就是双圆弧算法的核心意义所在。
除了两端点坐标约束之外,算法还引入端点的切线向量作为额外的几何信息,为简化计算,这里起点和终点切线方向向量可由NURBS曲线特定控制顶点以给定参数形式确定。由端点坐标Ps、Pe和切线向量Ts、Te获得曲线的切向圆弧来逼近原始曲线,进而完成曲线精插补。基于双圆弧的NURBS曲线插补流程如图2所示。

图2 双圆弧插补流程图
3 NURBS曲线插补速度波动问题理论分析与算法验证
3.1 理论分析
传统上利用NURBS曲线插补技术产生曲线的一般方法是:利用参数值uk+1=uk+Δu来进行迭代进而完成粗插补运算。通常,在粗插补运算过程中,参数曲线插补器常用的结构包括等参数插补、等速度插补、具备速度规划特征的插补三种方式。Bedi等[10]最早提出均匀增加参数值的方式,即 Δu为一常数。该方法形式简单,便于实现,由于参数域空间与笛卡儿空间的不一致性,参数的等间隔距离选取并不能保证曲线位置也等间隔分布。所以参数域内的等间隔造成了相邻插补区域之间的插补距离不等,造成进给速度的严重波动。
文献[11]较早提出利用泰勒展开关系式来获得较为精准的uk和uk+1之间的关系。由曲线定义可知,任意时刻曲线速度为
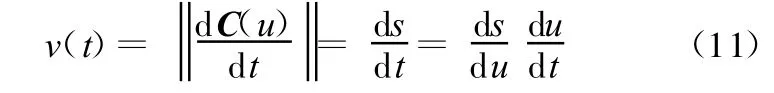
式中,s为位移。
相应地,参数u对t的微分可表示为

式中,x′、y′、z′均为相对 u 之微分。

合并式(12)和式(13)则可以得到直接解出式(14)较为困难而且计算量很大,
这里利用差分近似的方式给出离散形式解:

式中,T为插补周期。
为减小计算量,可以采用一阶或者二阶泰勒展开近似。由第2节定义,一阶和二阶泰勒展开分别为

一般来说,进行到二阶泰勒展开已可满足大多数工程应用,此时高阶项的影响已可忽略不计。另外也可看到,为了获得参数值的二阶泰勒展开,需要进行大量的数据运算,包括求取一阶和二阶导数,这给相关应用带来了很大困难,迫使在具体使用时往往需要在精度和速度之间作出平衡。
在研究上述传统数值计算方法的同时,本文拟结合控制思想,研究一种基于数值反馈特性的自适应插补的思想和策略,即利用学习迭代的思想,对每一个uk+1进行n次学习迭代u(n)k+1,给予一定的收敛条件判断,当时,结束迭代,从而得到需要求得的参数值uk+1,并且可以证明,这种方法获得的收敛值是唯一的。该算法思想如下:直接采用式(17)生成参数u显然可以带来较为理想的精度,然而将带来沉重的计算负荷。为简化计算,我们引入差分算子来代替相应的一阶和二阶微分算子,由文献[8]可得

代入式(17)得

这种以差分代替微分的离散化表达方式显然大大利于简化数值计算,但也引起了较大的截断误差。为此,本文采用了先采用离散差分简化计算,进而利用学习迭代运算来控制误差幅度的自适应插补策略。相应的学习迭代运算过程表述如下:

式中,uk为参数变量u在tk时刻的值;u(
kn+)1为参数变量u在tk+1时刻经过n次迭代运算后的值;β为0至1之间的一个常数;vk*为命令指定速度;v(kn-1)为经过n-1次迭代后所计算的当前速度。
相应的学习迭代终止条件为

3.2 算法分析与实际验证
对于NURBS一类复杂曲线造型问题,在完成参变量uk求取(即粗插)之后,采用何种方法来完成精插工作才是系统的关键所在。对于此问题的研究,直线和圆弧是工程上常用的两种基本逼近手段,在大多数文献中已有较全面的论述。基于不同应用考虑,有的研究者从曲线整体光滑性角度研究NURBS曲线逼近[12],也有学者从曲线特征提取的角度研究样条曲线逼近[13]。20世纪90年代以来,由于双圆弧的一些几何上的优异特征,相关学者相继引入双圆弧来表征一些复杂形状的曲线,如对平面抛物线的逼近[14]、对任意空间点序列的逼近[15]。但大多数研究仅仅停留在理论分析的层面上,具体应用于实际工程的案例极少。
考虑到上述因素,算法验证与实验实施环节主要就以下几个问题展开说明:首先研究所论及的插补算法应用于实际系统的可行性,基于双圆弧逼近的曲线插补方式,给出具体曲线造型分析说明,给出原始生成的G代码,并给出曲线实际轨迹加工结果;然后,对所讨论的速度波动抑制的若干策略给出较为详尽的分析,分析各种算法优劣,同时也进行实际系统加工测试。
3.2.1 NURBS曲线插补可行性测试
可行性测试实验采用大多数研究者经常采用的不规则复杂图形双翼蝴蝶作为系统验证的实验对象,采用常见的CAM 软件如RhinoScript或ProE等辅助设计软件获得被测图形的G代码描述(图3)。图3中,P代表权重,X、Y为控制节点,KNOT由程序自动求出。上述几段G代码分别描述了双翼蝴蝶的两翼、触须及各连接部分。

图3 双翼蝴蝶G代码描述
为了进一步验证算法的可行性,本文在自行开发的基于RTLinux的先进数控平台上进行了系统整合和实际加工实验。系统采用基于PC平台的开放式数控系统平台[16]、实时操作系统,机械本体采用自行开发的三维立式微型铣床(图4),控制接口采用自制的PC104运动控制卡。采用铅笔来记录数控系统的运行轨迹。相应软件仿真和实验运行结果分别如图5、图6所示。

图4 机械本体

图5 软件仿真

图6 实际轨迹
3.2.2 速度波动抑制算法实际应用
如上所述,由于参数曲线构造本身存在一定的缺陷性,即由于参数域空间与笛卡儿空间的不一致性,参数的等间隔距离选取并不能保证曲线位置也等间隔分布,从而造成进给速度的严重波动。目前的解决方法大多是采用适当的数值修正算法来抑制或减小这种误差。本文就上述一阶泰勒展开、二阶泰勒展开和具有数值反馈特性的自适应插补策略三种数值修正算法给出具体分析和相应的实验结果。
测试对象为二阶NURBS曲线造型“Ω”,其相应控制参数如表1所示,相应的曲线形状和实际加工轨迹如图7、图8所示。
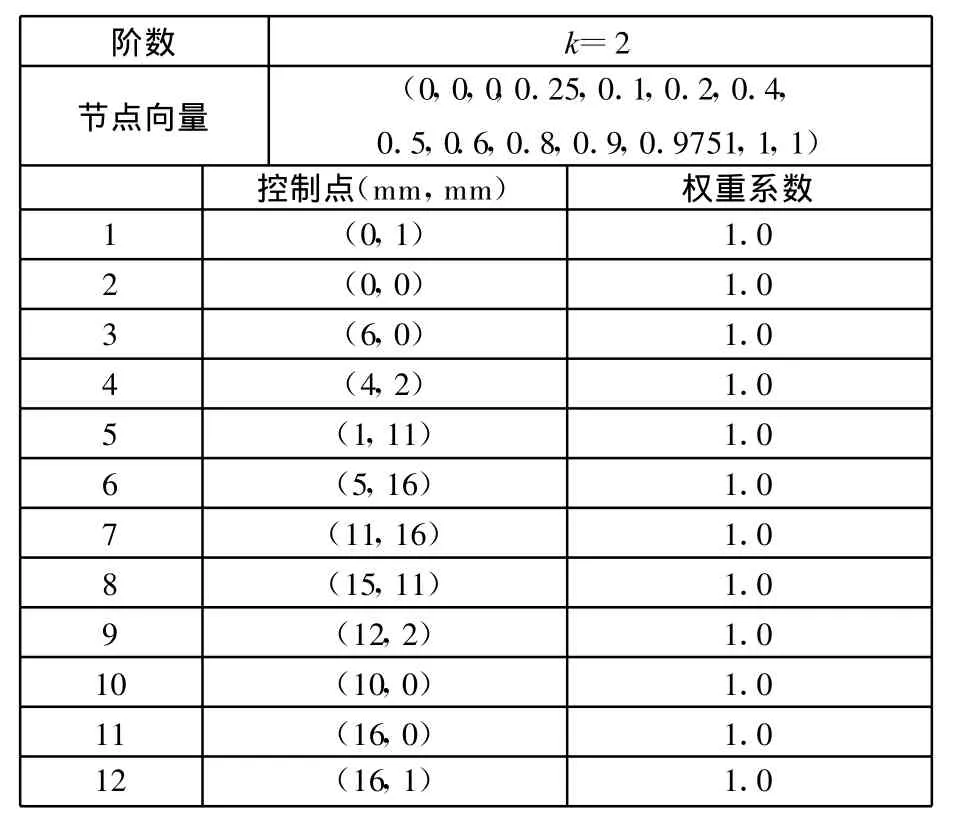
表1 NURBS曲线参数表
采用3.1节算法,分别采用一阶泰勒展开、二阶泰勒展开、自适应插补等几种方法考察实际系统运行中速度波动情况。相应运行参数为:插补周期2ms,运行速度10mm/s。相应系统曲线造型预览和速度波动情况如图7和图9所示。从图9可以看出,二阶泰勒展开、自适应插补展开均比一阶泰勒展开有很大改善,相对速度误差(相对速度误差为给定速度减去实际速度然后再除以给定速度)从一阶泰勒展开的最大2%减小到自适应插补模式下的0.05%。当然,实际系统设计还要考虑算法的收敛性和运算效率,这里不再赘述。

图7 曲线造型

图8 实际加工轨迹
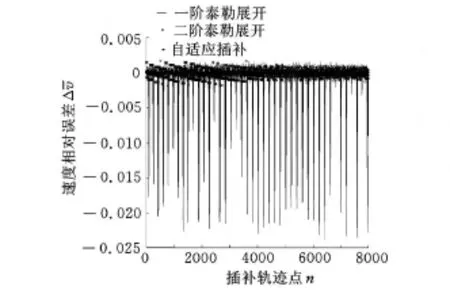
图9 速度波动抑制算法比较示意图
4 结语
复杂曲线构成机理一直是目前CAD/CAM领域研究的热点。本文利用双圆弧数值处理算法来逼近NURBS曲线,并对原有算法进行了简化和改进,取得了较为满意的运算效果。同时进行了相关实验和数值仿真,理论和实验都证明本文所提算法的可行性,研究成果已在实验室应用成功,可望进一步推广和应用。
[1] Piegl L,Tiller W.The NURBS Book[M].Berlin:Springer,1995.
[2] Yang D C H,Kong T.Parametric Interpolator Versus Linear Interpolator for Precision NC Machining[J].Computer-aided Design,1994,26(3):225-233.
[3] Yeh S,Hsu P.The Speed-controlled Interpolator for Machining Parametric Curves[J].Computeraided Design,1999,31(5):349-357.
[4] 彭芳瑜,何莹,李斌.NURBS曲线高速插补中的前瞻控制[J].计算计辅助设计与图形学学报,2006,18(5):625-629.
[5] Guo Wei,Du Daoshan,Xu Rongzhen,et al.Study on Real-time Look-ahead and Adaptive Parametric Curve Interpolator[J].Journal of Shanghai Jiaotong University(Science),2007,12(3):388-393.
[6] 李建刚,张婷华,李泽湘,等.一种完善的自适应NURBS曲线插补算法[J].中国机械工程,2008,19(9):1095-1102.
[7] 赵国勇,徐志祥,赵福令.高速高精度数控加工中NURBS曲线插补的研究[J].中国机械工程,2006,17(3):291-294.
[8] Lo C C.Feedback Interpolators for CNC Machine Tools[J].Journal of Manufacturing Science and Engineering,1997,119(4):587-592.
[9] Piegl L,Tiller W.Biarc Approximation of NURBS Curves[J].Computer-aided Design,2002,34(11):807-814.
[10] Bedi S,Ali I,Quan N.Advanced Interpolation Techniques for CNC Machines[J].ASME Journal Engineering Industry,1993,115:329-336.
[11] Tsai Miching,Cheng Chungwei.A Real-time Predictor-corrector Interpolator for CNC Machining[J].Journal of Manufacturing Science and Engineering,2003,125(3):449-460.
[12] 史利民,王仁宏.NURBS曲线曲面拟合数据点的迭代算法[J].数学研究与评论,2006,26(4):735-743.
[13] 周红梅,王燕铭,刘志刚,等.基于最少控制点的非均匀有理B样条曲线拟合[J].西安交通大学学报,2008,42(1):73-78.
[14] 张莉彦,邱辉,陈虎.平面曲线的双圆弧最佳逼近[J].组合机床与自动化加工技术,2002(3):32-34.
[15] 林杰.空间点列的双圆弧逼近[J].福建工程学院学报,2008,6(6):742-744.
[16] 史旭光.面向数控设备的实时Linux系统构建与应用[J].机床与液压,2007,35(7):19-24.

