基于支持向量机的数控机床空间误差辨识与补偿
吴雄彪 姚鑫骅 何振亚 傅建中
1.金华职业技术学院,金华,321017 2.浙江大学,杭州,310027
0 引言
在数控机床上实现高精度加工的关键是提高机床的空间定位精度。计算机实时误差补偿技术是一种经济而有效的方法,该方法在不改变机床结构和制造精度基础上,通过对机床加工过程的误差源进行分析、建模,实时地预测加工点的空间位置误差,将该误差量反馈到数控系统中以进行误差修正,从而提高机床空间位置精度。误差补偿是提高数控机床加工精度的有效途径,其实现的关键技术之一是如何精确地建立数控机床空间误差预测模型。
近年来,国内外在数控机床空间误差检测与补偿方面做了大量的研究工作[1-2]。在机床空间误差检测方面,Wang[3]提出了激光矢量分步对角线法以快速测量除旋转误差外的其他12项机床元素误差,包括3个定位误差、6个直线度误差和3个垂直度误差;Du等[4]提出了平面正交光栅多步检测三轴加工中心的空间位置误差的方法。在空间误差建模与预测方面,已有许多方法如三角几何法、误差矩阵法、刚体运动学法、多体系统理论法[5]和神经网络法[6]等,能够用于空间误差模型的建立。本文采用激光矢量分步对角线法检测与辨识空间误差,进而建立基于支持向量机(support vector machine,SVM)的数控机床空间误差预测模型,在一台数控铣床上进行误差辨识和补偿实验研究,结果表明支持向量机预测模型能有效辨识数控机床的空间误差。
1 数控机床空间误差建模
由刚体运动学原理可知,刚体在三维空间有6个自由度,即每一个轴向运动都存在6个误差;同时,每个轴之间并不垂直,3个轴两两就有3个垂直度误差。因此,对于任一类型的3轴数控机床都有21项误差元素:①直线定位误差δx(x)、δy(y)和 δz(z);② 直 线 度误 差 δy(x)、δz(x)、δx(y)、δz(y)和 δx(z)、δy(z);③转角误差 εx(x)、εy(x)、εz(x)、εx(y)、εy(y)、εz(y)、εx(z)、εy(z)和εz(z);④垂直度误差εxy、εxz和εyz。
根据多体运动理论,分别在床身、工作台和运动轴上建立坐标系,通过建立齐次坐标变换矩阵,建立刀具和工件之间的误差方程,最后可得到立式数控铣床的空间误差模型[7]:
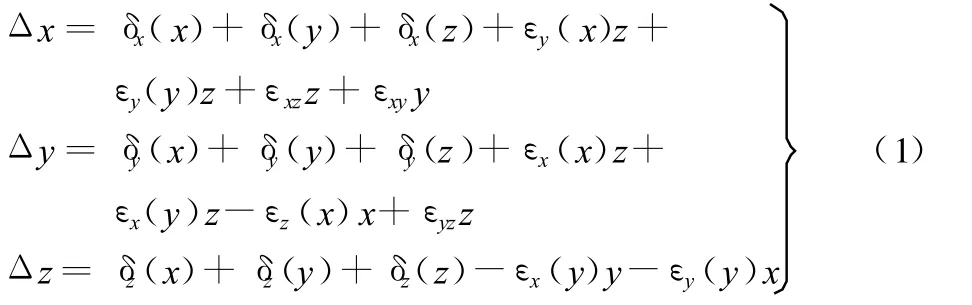
对上面的建模结果进行分析后知,一台3轴数控机床的误差可以归结为在空间3个方向的误差Δx、Δy和Δz,这3个误差和机床x、y和z方向的运动有关,如果重新记为Ex(x,y,z)、Ey(x,y,z)和Ez(x,y,z)(其中,下标 x、y、z 为误差的方向,括号内的 x、y、z为运动方向),则

可以看到,以上9项误差综合了各个误差元素,因此在进行误差补偿时无须求得具体的21项误差元素,而可以通过用激光分步对角矢量测量方法测量机床工作空间立方体的4条体对角线误差直接得到这9项误差,进而建立空间误差模型[7]。
2 基于支持向量机的空间误差预测模型
在实际利用激光干涉仪进行数控机床误差检测时,只能按一定的坐标位置间隔离散地检测出各空间误差的大小。对于测量点间的误差预测,目前主要通过线性插值或神经网络(ANN)计算来确定。但由于实际测量的空间误差数据中或多或少存在一定的噪声,直接利用这些误差数据进行线性插值时,等于对噪声也进行了叠加而不是均化,造成预测值波动较大,泛化性不好,从而影响误差补偿精度。神经网络方法的优化目标是基于经验的风险最小化,这只能保证学习样本点的估计(分类)误差最小,而不能保证预测的效果达到最优,且神经网络权系数的调整方法存在局限性,神经网络容易陷入局部最优并过分依赖学习样本。而支持向量机基于结构风险最小化原则,较好地解决了小样本、非线性、高维数、局部极小点等实际问题,已在模式识别、信号处理、函数逼近等领域得到了应用。Suykens等[8]提出了最小二乘支持向量机(LS-SVM)方法,采用最小二乘线性系统作为损失函数,将不等式约束改为等式约束,求解过程变成了解一组等式方程,求解速度相对加快。本文引入 LS-SVM 方法,针对机床空间误差特性与建模需求进行参数优化,为解决空间误差预测中存在的问题提供一种可行的有效途径。
LS-SVM的空间误差预测问题描述为求解如下问题:
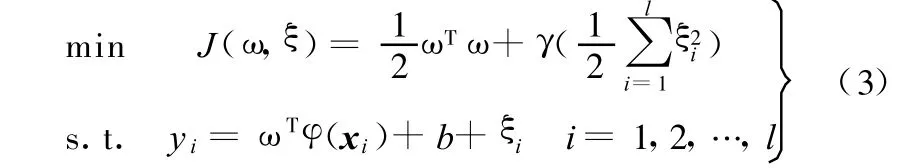
式中,xi为坐标输入量;yi为预测目标值;ξi为残差变量,ξi∈ R;φ(◦)为核空间映射函数,φ(◦):Rn→Rnh;ω为权矢量,ω∈ Rnh;γ为可调参数;b为偏差量。
引入拉格朗日函数:

式中,αi为拉格朗日乘子。
根据极值存在的必要条件,得到如下方程组:

式(5)消去 ω和ξ,得到

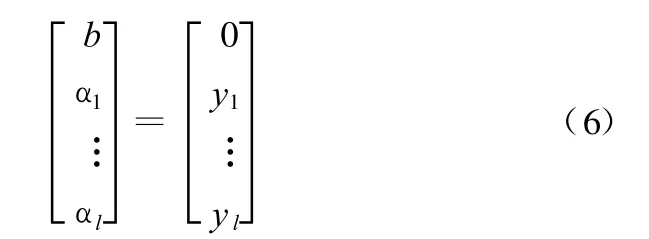
根据Mercer条件[8],使用核函数K(x,xi),LS-SVM回归估计可表示为如下形式:

其中,α、b由式(6)求解出。核函数K(x i,x j)为满足Mercer条件的任意对称函数,常采用径向基函数(RBF)核函数:K(x i,x j)=exp[-(x ixj)2/(2σ2)],它只有一个待定参数σ,其值越大,收敛速度越快。对于采用径向基核函数的LSSVM,主要参数是正则化参数γ和核函数宽度σ,这两个参数在很大程度上决定了LS-SVM的学习和泛化能力。
3 空间误差检测与补偿实验
在一台3轴立式小型数控铣床上进行空间误差检测及补偿实验(图1)。机床测量空间范围为200 mm×200 mm×120 mm。采用激光分步对角矢量测量方法,应用激光多普勒位移测量系统(LDDM),对机床工作空间立方体的4条体对角线进行分步矢量测量,从而得到比传统的对角线测量多 3倍的数据,为误差的分离提供足够的数据。

图1 激光分步对角矢量测量实验
如图2所示,机床共有4条体对角线,分别为PPP/NNN 、NPP/PNN 、PNP/NPN 、PPN/NNP。其中,P表示沿坐标轴正方向运动;N表示沿坐标轴负方向运动。

图2 空间体对角线定义
以体对角线PPP为例(图2),测量步骤如下:把机床工作空间x、y和z轴分成n等份,安装在主轴上的移动光靶(平面反射镜)从起始点开始,沿x方向移动一个步距后暂停,暂停过程中采集数据;然后沿y方向移动一个步距后暂停,采集数据;最后在z轴方向移动一个步距后暂停,采集数据。重复上述步骤一直移动到体对角线的另一端点。
通过LS-SVM方法进行数控机床的体对角线误差建模,选用 RBF核函数,其中,参数γ=56.2,σ2=0.2。采用LS-SVM 方法对样本数据进行训练、建模,即可得空间误差预测模型。图3、图4所示为补偿前体对角线误差实测值及神经网络(ANN)、LS-SVM预测值。图5、图6所示为补偿后机床体对角线误差的变化。可见,各条对角线的误差在补偿后最大值都减小到了10μm以内,补偿效果显著。为了进一步定量评价神经网络与LS-SVM两种预测方法的精度,常使用平均绝对百分比误差(MAPE)这个性能指标,其定义为
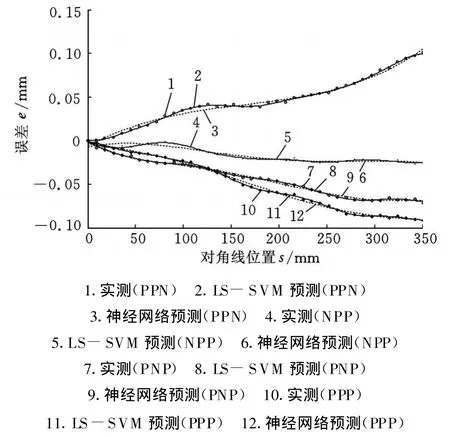
图3 补偿前正向体对角线误差实测值及神经网络、LS-SVM预测值

式中,li、lˆi分别为实测值与预测值。

图5 补偿后正向体对角线误差

图6 补偿后反向体对角线误差
表1所示为两种方法的比较结果,可以看出,LS-SVM方法的建模精度较神经网络有所提高,在建模速度上则具有显著优势。
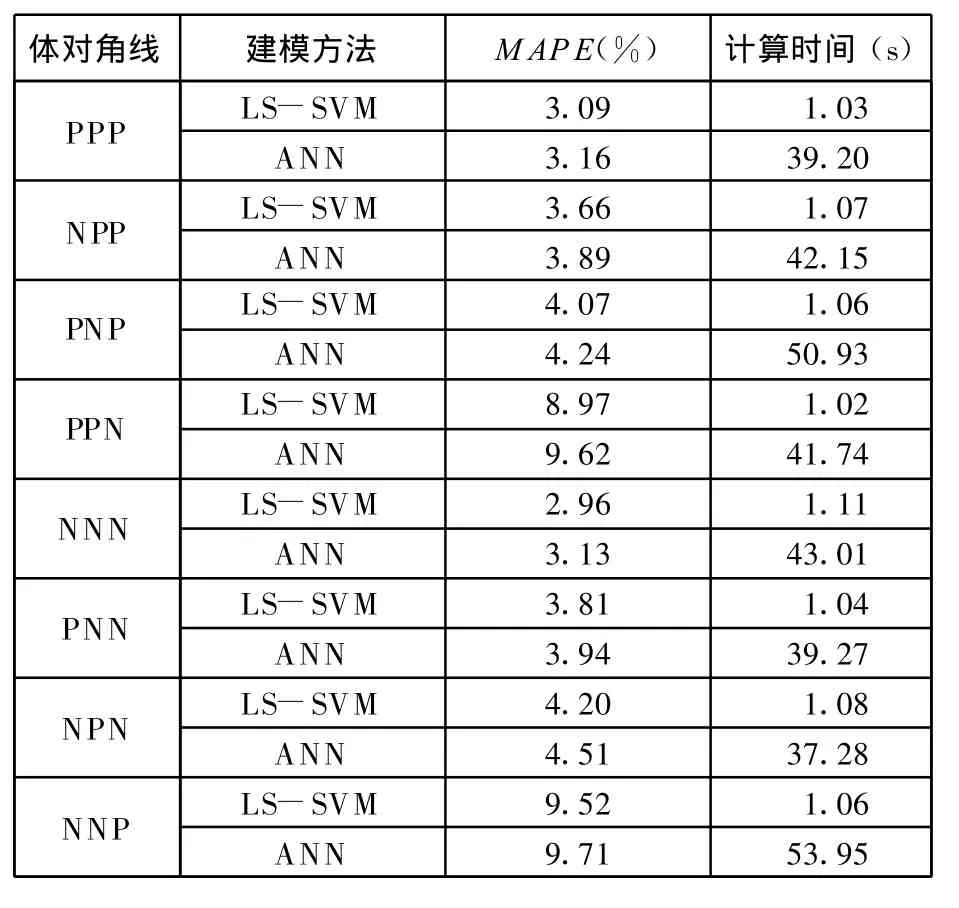
表1 LS-SVM建模与神经网络建模方法比较
4 结论
对数控机床空间误差进行预测与补偿可有效地提高数控机床的位置精度。本文提出基于支持向量机的数控机床空间误差辨识与补偿方法,通过训练学习,优化最小二乘支持向量机参数,可有效获得数控机床空间误差的预测模型。补偿实验结果表明,支持向量机空间误差预测模型补偿精度高、建模速度快,通过其补偿可有效地提高数控机床的精度。
[1] Ramesh R,Mannan M A,Poo A N.Error Compensation in Machine Tools—a Review Part 1:Geometric,Cutting-force Induced and Fixture-dependent Errors[J],Int.J.Mach.Tools Manufacturing,2000,40(9):1235-1256.
[2] 张虎,周云飞,唐小琦,等.数控机床空间误差的无模测量与补偿[J].华中科技大学学报(自然科学版),2002,30(1):74-77.
[3] Wang C.Laser Vector Measurement Technique for the Determination and Compensation of Volumetric Positioning Errors.Part I:Basic Theory[J].Review of Scientific Instruments,2000,71(10):3933-3937.
[4] Du Z C,Zhang S J,Hong M S.Development of a Multi-step Measuring Method for Motion Accuracy of NC Machine Tools Based on Cross Grid Encoder[J].International Journal of Machine Tools and Manufacture,2010,50(3):270-280.
[5] 粟时平,李圣怡,王贵林.基于空间误差模型的加工中心几何误差辨识方法[J].机械工程学报,2002,38(7):121-125.
[6] John M F,Arvin A.Machine Tool Positioning Error Compensation Using Artificial Neural Networks[J].Engineering Applications of Artificial Intelligence,2008,21(7):1013-1026.
[7] 沈金华,杨建国,王正平.数控机床空间误差分析及补偿[J].上海交通大学学报,2008,42(7):1060-1063.
[8] Suykens J A K,van Gestel T,de Brebanter J,et al.Least Squares Support Vector Machines[M].Singapore:World Scientific Pub.Co.,2002.

