支撑结构多目标拓扑优化设计研究

方子帆 杨 磊 杜道佳 何孔德 张 屹

三峡大学水电机械设备设计与维护湖北省重点实验室,宜昌,443002

0 引言

支撑结构是一个复杂组合结构,承受着被支撑物的所有动态载荷和静态载荷,其结构的设计对于整个装置的性能起着重要的作用。支撑结构在传统设计中,没有考虑结构在运行过程中载荷与约束的变化,并且为保证其安全性,设计的结构刚度、强度有较大富余,这样浪费了材料,增加了整体重量。为了改进设计方法,得到更优的结构形式,在综合考虑多工况的基础上进行了多目标的结构优化设计,在确保支撑结构强度、刚度的前提下,使得结构轻量化,达到减少材料用量,降低制造成本的目的。

结构优化设计有设计变量、约束条件和目标函数三要素。根据设计变量的不同,可分为尺寸优化设计、形状优化设计和拓扑优化设计三个层次,尺寸优化是选取结构元件的几何尺寸作为设计变量;形状优化是选取结构的几何特征作为设计变量;而拓扑优化则是选取结构的相对密度作为设计变量。优化的层次越高,优化工作越难。Mlejnek等[1]从工程角度出发提出了结构材料密度的幂次惩罚模型,通过在0～1离散结构优化问题中引入连续设计变量,并加入中间密度惩罚项,从而将离散结构优化问题转换为连续结构优化问题,这一方法构成了后来密度法材料插值模型的基础。Sigmund[2]对密度法材料插值模型进行了深入研究,从理论上研究了各种不同的密度法材料插值方法,提出了一种基于正交各向同性材料密度幂指数形式的变密度法材料密度插值理论,又称为SIMP理论。隋允康等[3]提出了一种独立连续映射模型方法,成功解决了多工况应力与位移约束下的桁架结构拓扑优化问题,并尝试将此方法推广到连续体结构拓扑优化中,研究了位移和应力约束下的连续体结构拓扑优化问题。本文以支撑结构为对象,通过建立优化设计的数学模型,研究了多工况下结构材料的最优布局和结构固有频率最大化的优化问题。

1 基于变密度法的拓扑优化数学模型

1.1 基于变密度法材料插值模型

变密度法是从均匀化方法[4]发展而来的,它定义了一个经验公式来表达每个单元的弹性模量与密度之间假定的函数关系,将材料的相对密度作为设计变量,结构的拓扑优化问题就转换为材料的分布问题。变密度法[5]通过引入惩罚因子,假想一种相对密度在0～1之间可变的材料,并在材料的弹性模量和单元相对密度之间建立起显式的非线性函数关系,当设计变量在(0,1)之间时,对中间密度值进行惩罚,使中间密度值逐渐向0/1两端聚集,将密度值趋近0的密度单元忽略,密度值趋于1的单元保留。

材料插值模型的惩罚函数定义为

式中,Ei(x)为第i个单元的密度;E0为单元满材料时的弹性模量;x为材料的相对密度;p为惩罚因子。

1.2 拓扑优化数学模型

在一定材料用量条件下,以密度函数来寻找最大刚度的结构材料最佳分布形式,以结构应变能为目标函数,体积为约束,相对密度为变量,基于变密度法的优化数学模型为

式中,x为设计变量,即式(1)中的材料相对密度;n为设计域中有限单元个数;C(x)为目标函数,表示结构的柔顺度;K为结构的总体刚度矩阵;U为结构的总体位移向量;F为结构所受的载荷向量;V为结构优化后的体积;vi为结构单元体积;p0为给定材料用量比率;V0为初始结构体积;V*为体积上限;xmin为最小相对密度。

1.3 多工况应变能拓扑优化函数

通过对式(2)的迭代,得到结构在体积约束下某单工况载荷作用下产生的最小静态应变能,结构的静态应变能C可以通过下式表示[6]：

可以认为应变能是结构刚度的倒数,当载荷给定后,结构的应变能越小则表示系统的刚度越大。应变能必须与静态子工况相关。当结构工作于多工况载荷时,每一个工况将对应一个刚度的最优结构拓扑,不同的载荷工况将得到不同的结构拓扑。因此,多工况拓扑优化问题属于多目标拓扑优化问题。用折中规划法[7]来研究多目标优化问题,构建的多工况拓扑优化目标函数为

式中,m为工况数;wk为第k个工况的权重;Ck(x)为第k个工况的子应变能优化目标函数;Cmkin为第k个工况子应变能目标函数的最小值,即在多目标问题中,只考虑其中一个目标函数,而暂不考虑其他子目标,但仍保留所有的约束条件得到的最佳解;Cmkax由优化迭代中第0步的初值得到。

1.4 多目标下的目标函数

多目标优化问题的目标函数[8]是一个由子目标构成的向量,用刚度和频率两个子目标作为优化主体,以体积作为约束,得到的多目标优化目标函数：

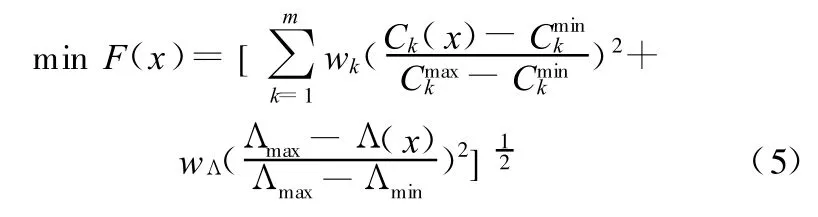
式中,Λ(x)为设置的第一阶固有频率优化变量;Λmax为单独对第一阶固有频率优化得到的最大值;Λmin为对优化前的原模型进行分析得出的最小值。

2 模型算法与流程

2.1 子目标权重

分析层级法采用配对比较的方法,不同时比较所有的子目标,而是将子目标两两比较,形成配对比较矩阵。

本文中有四个子目标(三个刚度子目标A1、A2、A3和一个频率子目标A4)的多目标优化问题,假设这四个子目标的重要性权重分别为 α1、α2、α3、α4。先比较出各个子目标重要性权重的两两相互比值,然后以这些比值作为元素,建立配对比较矩阵：

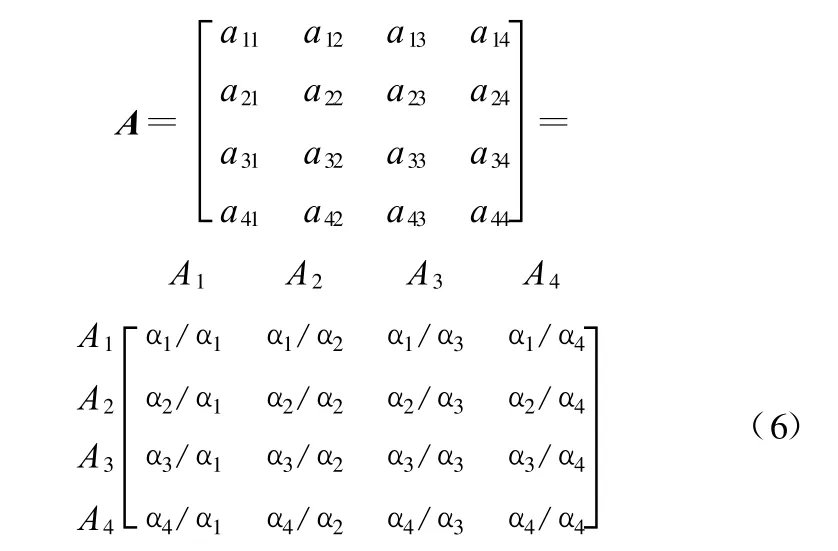
其中,矩阵A的元素aij(i,j=1,2,3,4)即为子目标Ai对A j的重要性比重的比值。可以发现,此比较矩阵是一对称矩阵,对角线元素全为1,且此矩阵中的元素不具有一致性,即 aik=αi/αk≠(αi/αj)◦(αj/αk),这种不一致性更加符合实际情况,且对主观重要性的测量有“校调”作用。

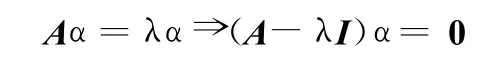
将配对比较矩阵A右乘一个由所有子目标重要性权重值组成的向量 α=(α1,α2,α3,α4)T,则有：由上式可知,所有子目标重要性比重值所组成的向量α即是矩阵A的特征向量,求出此矩阵最大特征值对应的特征向量,就是所要求的各子目标的重要性的权重。

设三个刚度子目标 A1、A2、A3和频率子目标A4相互间两两比值分别为

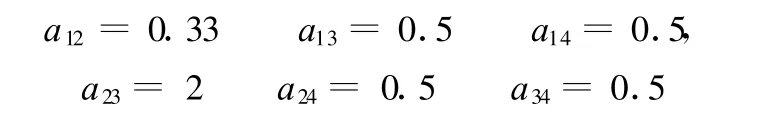
则配对比较矩阵为

求出的矩阵最大特征值为λmax=4.14,对应的特征向量为α=(0.22,0.55,0.34,0.72)T,此特征值即为四个子目标重要性的权重值。

2.2 结构拓扑优化迭代过程

在建立的材料插值模型基础上,基于优化准则法的结构拓扑优化求解流程如图1所示。

图1 基于变密度法的拓扑优化流程图

3 实例研究

以某俯仰装置支撑结构为对象,初始结构如图 2所示,上板长 1300mm,宽 1000mm,厚40mm,侧板厚20mm,结构材料为Q235钢。

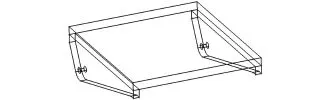
图2 初始结构模型

3.1 边界条件

俯仰装置在一个运动周期内是一个动态的过程,受到动态载荷的作用。本文分析俯仰运动中三个典型工况,通过动力学软件提取载荷的最大值,作为静态载荷加载在结构上,进行静态应变能工况优化。三个工况分别是支架水平 0°、俯仰75°、俯仰37°。三个工况的载荷和约束情况如表1、图 3 所示。

表1 三个工况下的载荷和约束

图3 三个工况的载荷和约束情况

3.2 有限元模型的建立及分析结果

利用HyperWorks10.0软件的Hypermesh前处理模块进行有限元处理,然后在OptiStruct优化模块环境下进行优化。根据支撑结构的板结构特点,将板壳结构通过抽取中面成为面单元,然后对面单元赋予厚度属性,这样可以提高计算结果精度和运算速度。

表2为优化前后的结果性能指标,图4所示为多目标评价函数的迭代历程,图5所示为结构拓扑优化结果。

表2 优化前后结构性能指标对比

图4 多目标函数迭代历程

4 结论

(1)经过拓扑优化,结构在三个工况下的静态应变能都得到了降低,对应的刚度得到了提升,一阶固有频率得到了提升,更加远离了共振频率区。

图5 拓扑优化结果

(2)采用多目标的拓扑优化方法,能从多个角度较为全面地考虑结构的工作状态,有效降低单一工况优化造成的设计风险。

(3)结构多目标拓扑优化方法适用于板壳类结构的优化设计,具有一定的工程应用价值。

[1] M lejnek H P,Schirrmacher R.An Engineering Approach to Optimal Material Distribution and Shape Finding[J].Computer Methods in Applied Mechanics and Engineering,1993,106：1-26.

[2] Sigmund O.Design of M aterial Structures Using Topology Optimization[D].Lyngby：Technical University of Denmark,1994.

[3] 隋允康,任旭春,龙连春,等.基于ICM 方法的刚架拓扑优化[J].计算力学学报,2003,6(20)：286-289.

[4] Bendsoe M P,Kikuchi N.Generating Optimal Topologies in Structure Design Using a Homogenization Method[J].Computer Methods in Applied Mechanics and Engineering,1988,71(1)：197-224.

[5] Bendsoe M P,Sigmund O.Topology Optimization：Theory,Methods and Applications[M].New York：Springer,2003.

[6] 张胜兰,郑冬黎,郝琪,等.基于 Hyper Works的结构优化技术[M].北京：机械工业出版社,2007.

[7] Zeleny M.Compromise Programming[C]//Cochrane J L,Zeleny M.Multiple Criteria Decision M aking.Columbia：University of South Carolina Press,1973：262-301.

[8] 范文杰,范子杰,苏瑞意.汽车车架结构多目标拓扑优化方法研究[J].中国机械工程,2008,19(12)：1505-1057.