多尺度全方位复合广义形态边缘检测的算法

曹 珩,杨述斌,罗 帆,贺 玺

(武汉工程大学电气信息学院,湖北 武汉 430074)

0 引 言

边缘是图像目标与背景之间的分界线,它是图像的基本特征之一,边缘的确定与提取对于整个图像场景的识别与理解非常重要.边缘检测是目标特征提取、识别和跟踪的基础[1],故而是自动目标识别技术(ATR)的核心内容之一,在计算机视觉、图像处理与分析、模式识别等方面发挥巨大作用,广泛应用于遥感、医学图像识别、图像编码、文档处理等诸多图像处理领域.

边缘检测主要利用目标与背景之间存在某种图像特征上的差异(例如灰度、颜色或者纹理结构等)来实现的,实质上就是检测图像特征发生变化的区域.利用边缘处灰度的不连续性,可以采用经典的空域微分算子[2](如sobel、LOG或Canny算子等)做卷积来进行边缘检测.经典的边缘检测算子算法简单快捷,但这些算法对于噪声敏感,而且效果不甚理想.随着人工智能的迅猛发展,诸如基于数学形态学、基于神经网络、基于小波分析等边缘检测算法不断涌现.相对经典的边缘检测算子而言,基于数学形态学的检测算法获得的边缘更为光滑连续、抗噪性能更好,从而得到广泛的应用.利用数学形态学检测时结构元素的选取决定了边缘检测的性能,鉴于基本的边缘检测算子采用单一的结构元素难以满足图像处理的要求,本文提出一种基于多尺度全方位的复合广义形态边缘检测算法,在抗噪性能与检测效果方面都能满足要求.

1 数学形态学基础理论概述

数学形态学诞生于1964年,是一门建立在数学基础上用集合论方法定量描述几何结构的新兴学科,可用于分析几何形状与结构,在图像处理领域中作用巨大.数学形态学用于几何结构分析的基本思想是运用一定形状的结构元素对图像做出度量和提取,从而分析和识别图像[3-4].

设一幅灰度图像为F(x,y),结构元素为B(i,j),则灰度形态学最基础的两种运算(膨胀和腐蚀)定义为膨胀运算

(F⊕B)(x,y)=

max{F(x-i,y-j)+B(i,j)}

(1)

腐蚀运算

(FΘB)(x,y)=

min{F(x+i,y+j)-B(i,j)}

(2)

将膨胀运算和腐蚀运算进行不同次序的组合运算,可以分别定义为开运算

F∘B=(FΘB)⊕B

(3)

以及闭运算

F·B=(F⊕B)ΘB

(4)

可以知道膨胀运算是局部极大值滤波,可以去除比结构元素小的暗点;腐蚀运算是局部极小值滤波,可以去除比结构元素小的亮点;开运算会消除边缘毛刺与孤立斑点,同时平滑较大物体的边界;闭运算可以填充较小的空洞与裂缝,同时平滑边界.由于膨胀会扩张图像,腐蚀会缩小图像,从形状上来说有

F⊕B≥F·B≥F≥F∘B≥FΘB

(5)

数学形态学在图像边缘检测中的基本思想是运用一定的结构元素对图像进行膨胀或腐蚀运算,膨胀的结果和原图像相减可以得到边缘图像,或是用原图像减去腐蚀的图像以得到边缘.由上述基本思想以及式(5)可以得到三种形态学梯度(即最基本的边缘检测算子[4])如下所示:膨胀型算子

Ed=F⊕B-F

(6)

得到的边缘为图像的外边缘;腐蚀型算子

Ee=F-FΘB

(7)

得到的边缘为图像的内边缘;膨胀腐蚀型算子

Edec=F⊕B-FΘB

(8)

得到的边缘为图像位于实际欧氏边界上的边缘.这些基本的检测算子结构简单,执行速度快,实质上是传统的差分算子在一定意义上的推广.但由于采用单一的结构元素,故而抗噪性能有限,只能适用于没有噪声的图像处理,难以达到边缘检测的性能要求.

同时对于这些基本的检测算子提取的边缘,其中膨胀型算子会使图像边缘变模糊;而腐蚀型算子会使图像边缘丢失一些细节;膨胀腐蚀型算子又会出现宽边缘现象,对于边缘的检测造成不利影响[5].为了解决这些问题,得到理想的图像边缘,可以采用复合型形态学梯度算法,对于基本的检测算子取

(9)

式(9)中α为一个适当的系数,取值范围为(0,1)之间的一个常数.由于Emn对于边缘细节具有一定的补偿作用,通过调节α的取值,可以叠加一部分图像细节[5],得到理想的图像边缘Eo,在减小图像边缘的模糊性并保留更多的边缘细节,同时还能抑制宽边缘现象.

针对单一结构元素的基本检测算子抗噪性能有限,利用开运算可以抑制正脉冲(峰值)噪声,闭运算可以抑制负脉冲(波谷)噪声,并且采用不同的结构元素来提取边缘,在式(6)～(8)的基本检测算子基础上加以改进,最终可以得到广义抗噪形态学算子[6]如下所示:

广义抗噪膨胀型算子

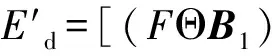
[(FΘB1)⊕B2]·B3

(10)

广义抗噪腐蚀型算子

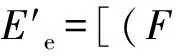
[(F⊕B1)ΘB2]ΘB3

(11)

广义抗噪膨胀腐蚀型算子

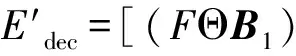
[(F⊕B1)ΘB2]ΘB3

(12)

广义抗噪型算子最大的优点是滤除噪声能力极强,但同时也存在模糊了图像边界的缺点.

2 算法设计与分析

广义抗噪型算子实质上是改进的抗噪型算子在一定程度上的推广.以广义抗噪膨胀型算子为例,如果取B1=B2=B,则退化为改进的抗噪膨胀型算子

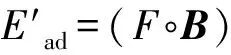
和抗噪膨胀型算子

EAD=F⊕B3-F·B3

相比较,可以看出改进的抗噪膨胀型算子中结构元素B主要起到滤波的作用,故而广义抗噪型算子中结构元素B1和B2主要起到滤波的作用,而B3主要起到提取相应的边缘的作用.查阅相关文献[3]可以知道形态学运算可以用于去除比结构元素小的噪声,故而检测算子选取较大的结构元素尺度会有很强的抗噪能力,有利于去除比结构元素尺寸小的噪声,但是边缘的细节会很粗略;选用较小的结构元素尺度会得到非常详细的边缘细节,但是因为只能去除比结构元素尺寸小的噪声,故而去除噪声的能力远远小于大尺度的结构.对于广义抗噪型算子在处理图像的过程中,可令起到滤波作用的结构元素B1、B2采用两种不同尺度交替滤波,则滤波时既能有效滤除噪声又有利于保持图像细节信息,这就是多尺度的思想.对于主要起到提取相应的边缘的结构元素B3,只是采用单一类型的结构元素对于与结构元素走向类似的边缘效果很好,但对于其余走向的边缘不敏感;故而难以处理复杂边缘的图形.如果B3分解为采用不同走向的结构元素例如B3i(i=1～4),其中B3=B31∪B32∪B33∪B34,由B3i所得的检测算子Ei就能对应检测不同方向上的边缘,有利于检测复杂的图像时得到相应方向上更详尽的边缘信息.随后对应的算子Ei进行相应的加权求和就能够对复杂的边缘获得较好的检测效果,这就是全方位检测的思想[7].结合多尺度与全方位的思想,就可以构造基于多尺度全方位的广义形态边缘检测算子如后文的式(13)～(15)所示.

然而基于多尺度全方位的广义形态边缘检测算子在滤除噪声时采用了多个不同的结构元素,很容易模糊图像的边缘.为了加强边缘信息,可以综合上一节提及的复合型形态学梯度算法的思想对多尺度全方位的广义形态边缘检测算法中的膨胀型、腐蚀型和膨胀腐蚀型算子进行复合处理,利用它们最大值与最小值之间的差值来补偿部分细节,用以解决边缘模糊的问题.

因而多尺度全方位复合形态边缘检测算法具体思路是结合上一节两种算法的优点,采用广义抗噪型算子并使用多尺度多结构元素[8]来提取边缘,最后结合复合型形态学梯度算法进行复合处理,从而得到一种检测效果较好的改进算法,不仅能够有效去除噪声,并且能够提取复杂的边缘,而且边缘不会出现模糊现象.该算法的具体步骤如下所示:

(1) 在广义抗噪型检测算子运算中,选取两种不同结构尺度的结构元素分别为十字结构B1=[0 1 0;1 1 1;0 1 0]及钻石结构B2=[0 0 1 0 0; 0 1 1 1 0;1 1 1 1 1;0 1 1 1 0;0 0 1 0 0](其中结构元素B1为3×3的矩阵,尺度较小故而边缘的细节会很详细,但是去除噪声的能力不佳;结构元素B2为5×5的矩阵,尺度较大故而有很强的去除噪声的能力,但是边缘的细节会很粗略),利用这两个不同尺度的结构元素在滤波时交替运算可以结合两者的优点,既能滤除噪声又能保持图像细节信息.选取方形结构B3=[1 1 1;1 1 1;1 1 1],分解为4个不同方向上的结构元素为B31=[1 0 0;0 1 0;0 0 1](矩阵里头元素‘1’与水平方向夹角为135度,有利于检测图像与水平方向夹角135度边缘),B32=[0 1 0;0 1 0;0 1 0](检测图像垂直方向的边缘),B33=[0 0 1;0 1 0;1 0 0](检测图像与水平方向夹角45度的边缘),B34=[0 0 0;1 1 1;0 0 0](检测图像水平方向的边缘);可以知道B3=B31∪B32∪B33∪B34,则分别利用这4个不同方向上的结构元素B3i(i=1～4)作为结构元素,有利于检测各个不同方向的边缘,同时结合两种不同尺度的结构B1及B2在去除噪声的同时保留图像细节,可以分别得到检测不同走向的多尺度全方位的广义形态边缘检测算子如下所示:

广义抗噪膨胀型算子:

EDi=[(FΘB1)⊕B2]⊕B3i-

[(FΘB1)⊕B2]·B3i

(13)

广义抗噪腐蚀型算子:

EEi=[(F⊕B1)ΘB2]∘B3i-

[(F⊕B1)ΘB2]ΘB3i

(14)

广义抗噪膨胀腐蚀型算子:

EDECi=[(FΘB1)⊕B2]⊕B3i-

[(F⊕B1)ΘB2]ΘB3i

(15)

(2)利用不同走向的广义形态边缘检测算子EDi(i=1～4)对提取的边缘进行加权求和得

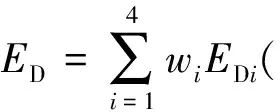
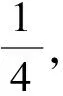
同理可得腐蚀型算子

膨胀腐蚀型算子

(3)采用复合型形态学梯度算法的思想,对于上述边缘算子,求得

(16)

式(16)中α为一个适当的系数,取值范围为(0,1)之间的一个常数.利用EMN对于边缘细节有一定的补偿作用,对于α进行适当调节,最终可以得到对应的边缘算子E,这样可以在加强边缘细节的同时又兼顾了边缘的清晰度.最后进行后期处理,将得到的边缘E二值化后再细化边缘,可以得到最终的边缘结果.

对算法进行分析可以知道,算法主体上采用广义抗噪型检测算子,故而对干扰噪声可以有效的进行滤除;由于算子采用了多尺度元素,可以在过滤噪声的同时保留了图像的主要细节;同时采用全方位的思想,因而对于具有复杂边缘的图像可以很好的进行边缘提取;最后通过复合型形态学梯度算法进行复合处理,减小了图像边缘的模糊程度,可以得到接近理想的单像素边缘的图像.故而该算法无论是在抗噪性能还是提取边缘的效果上都比基本的形态学算子有了很大程度上的提高,能够满足边缘检测的要求.

3 实验仿真结果

选取MATLAB软件进行仿真,分别以200×200大小的Lena及cameraman图像作为原始图像,再转化为灰度图像并增加了2%的椒盐噪声作为检测图像,随后采用各种不同的算子对图像进行边缘检测如图1～12所示.其中最基本的膨胀腐蚀型算子采用式(8);广义抗噪膨胀腐蚀型算子采用式(11);多尺度全方位复合广义形态边缘检测算子的选取参看上一节的内容,在仿真试验中通过试探发现α取0.3较为适宜.

图1 原始图像

图2 噪声图像

图3 sobel 算子

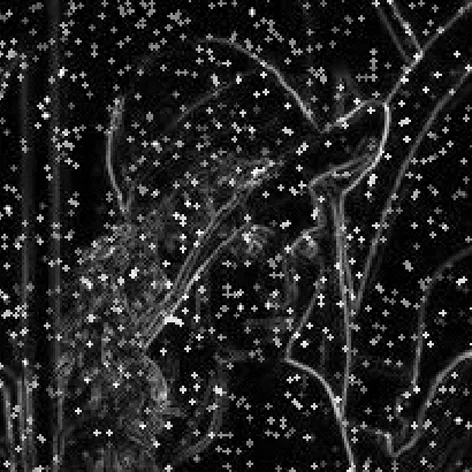
图4 基本的膨胀蚀型算子

图5 广义抗噪膨胀腐蚀算子

图6 本文提出的算子

图7 原始图像

图8 噪声图像

图9 sobel 算子

图11 广义抗噪膨胀腐蚀算子

图12 本文提出的算子

由仿真结果可以看出面对噪声的干扰时,经典的检测算子对于噪声非常敏感,不仅边缘不连续而且有很多漏检,难以分辨出边缘的轮廓;最基本的膨胀腐蚀型算子能够勉强得出大体上的边缘轮廓,但无法滤除噪声;广义抗噪膨胀腐蚀型算子虽然滤除了噪声干扰,但是边缘非常模糊并具有重影现象,对于部分细节没有清晰的表达;而本文提出的抗噪算子不仅对于噪声有着很好的抑制效果,并且所得的边缘接近理想的单像素宽,图像较为平滑,边缘的细节如面孔的描绘也较为清晰,效果较为理想.

4 结 语

以上提出了一种基于广义抗噪形态学算子的复合型检测算法,通过仿真可以看出,它不仅具有很强的抗噪性能而且能够有效地检测出较为复杂的边缘,所得的边缘更为完整连续,细节清晰度也更高,满足了边缘检测的各项基本要求,检测效果较为满意.故而所得算法是一种切实有效的边缘检测算法.

参考文献:

[1]龚声溶,刘纯平,王强.数字图像处理与分析[M].北京:清华大学出版社,2006.

[2]张小琳.图像边缘检测技术综述[J].高能量密度物理,2007,3(1):36-40.

[3]龚炜,石青云,程民德.数字空间中的数学形态学理论及应用[M].北京:科学出版社,1997.

[4]Haralick R M, Stemberg S R, Zhuang X.Image Analysis Using Mathematical Morphology[J].IEEE Trans Comput,1987,9(3):532-550.

[5]王芬芬,白秋果,王彪,等.基于多结构元素的形态学抗噪边缘检测算法[J].电子测量技术,2008,31(4):36-37.

[6]杨述斌,彭复员.噪声污染图象中的广义形态边缘检测器[J].计算机工程与应用,2002,38(17):91-92.

[7]杨述斌,陈艳菲,程莉.交替滤波的加权形态边缘检测算法[J].武汉工程大学学报,2009,31(7):88-90.

[8]刘清,林土胜.基于数学形态学的图像边缘检测算法[J].华南理工大学学报自然科学版,2008,36(9):113-116.