考虑切向摩阻力作用下弹性地基梁的内力计算

宋 征,祝启坤

(武汉工程大学环境与城市建设学院,湖北 武汉 430074)

0 引 言

Winkler弹性地基梁广泛存在于实际工程基础梁、格构锚固框架梁的内力计算.该模型假设地基上任意一点所受的法向反力P与该点的沉降量s成正比[1].

P=ks

(1)

式(1)中：k为基床系数，kN/m3;s为基底某点沉降量，mm.

Winkler地基模型如图1所示.

图1 Winkler地基模型

Winkler地基模型同时还假设沉降只发生在基底与刚性基座之间,而不考虑基底切向摩阻力的作用,因此,该模型只适用于地基土很薄或梁刚度较大的情况,而在实际工程中,当梁与地基倾斜接触或梁上有倾斜荷载时,地基与梁之间就存在切向摩阻力[2].本文试图在Winkler地基模型的基础上构建考虑切向摩阻力作用时梁的内力简化计算模型.

1 考虑切向力有限元计算模型

1.1 Winkler地基模型上梁有限元计算模型

首先将Winkler地基上梁简化为具有一系列弹性支座的连续梁如图2所示,然后将弹性支座用一根链杆来代替[3],如图3所示.

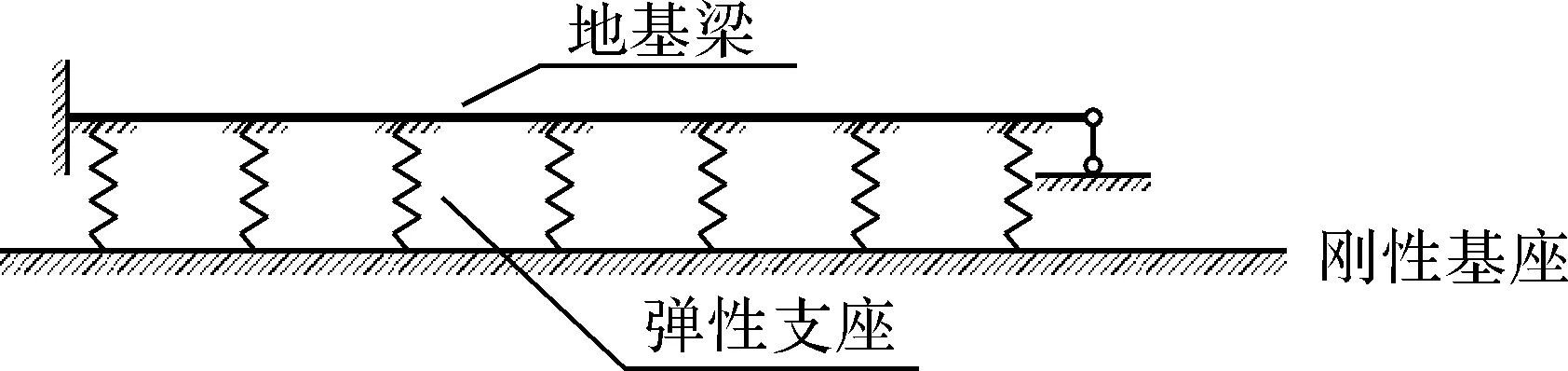
图2 具有弹性支座的连续梁

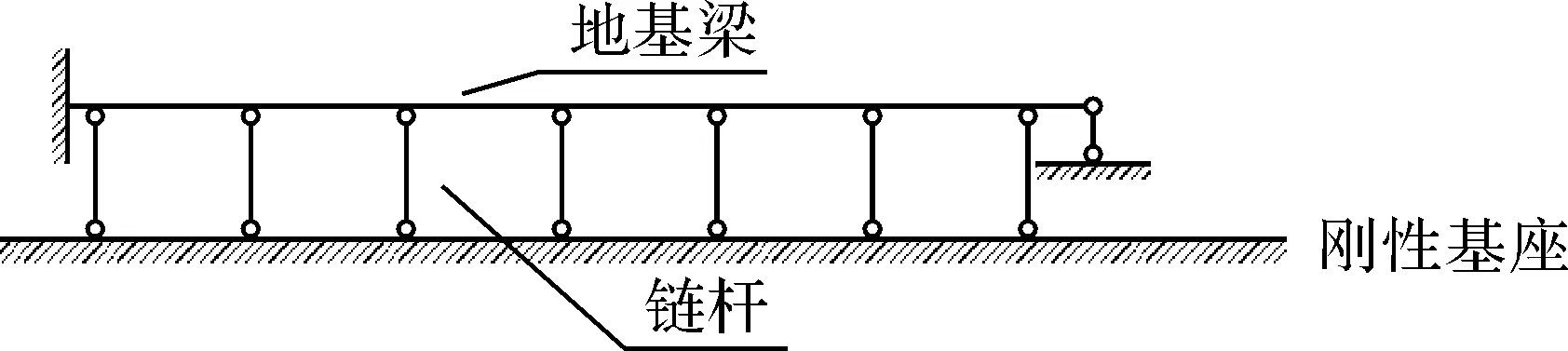
图3 简化计算图

其中代替弹性支座的链杆单元的杆长一般取与梁单元同量级的值,选取适当的截面面积A,使之与被代替的弹性支座等效.由于用链杆代替地基的变化情况,可将链杆的刚度系数取基床系数k.

令:

EsA/L=k

则可得:

A=Lk/Es

(2)

式(2)中:Es为土的弹性模量.

根据有限元分析,梁单元和链杆单元结构坐标系中的单元刚度矩阵可由(3)式求得:

(3)

其中

(4)

形成单元刚度矩阵[K](e)后,可由直接刚度法形成总体的刚度矩阵,然后计算出各单元结点力和结点位移.

1.2 考虑切向摩阻力梁的有限元计算模型

基于Winkler地基模型,将梁与地基切向摩阻力同样假设与梁的切向变形成正比[4-5]即:

τ=ksδ

(5)

式(5)中：ks为地基侧向系数,kN/m3;δ为梁的切向变形,mm.

在梁端引入水平的弹簧来模拟切向摩阻力q,如图4所示.

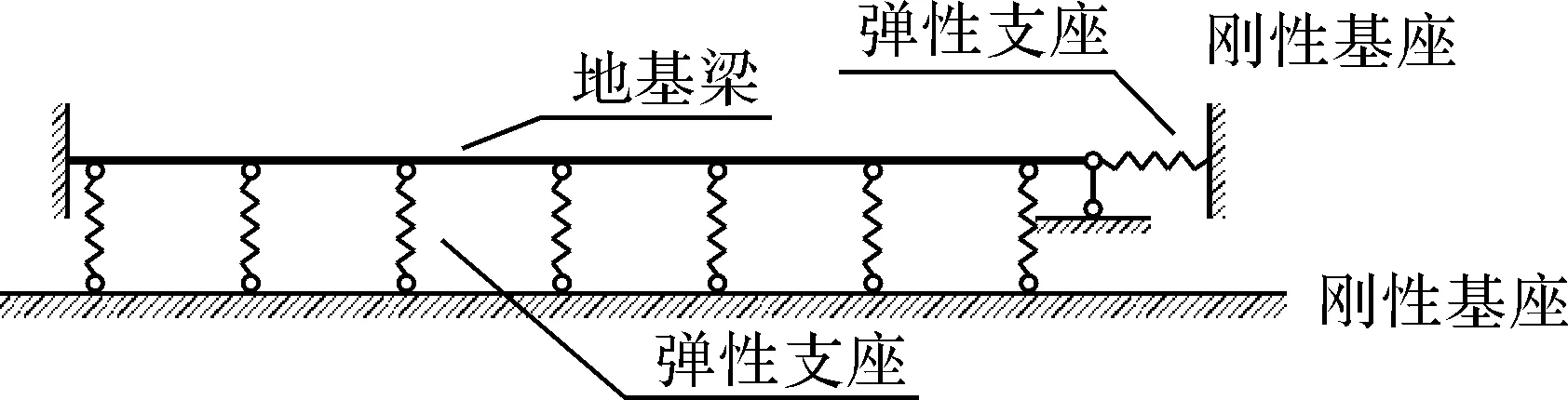
图4 考虑切向力梁的计算模型

同样将水平弹性支座用一链杆代替,如图5所示.

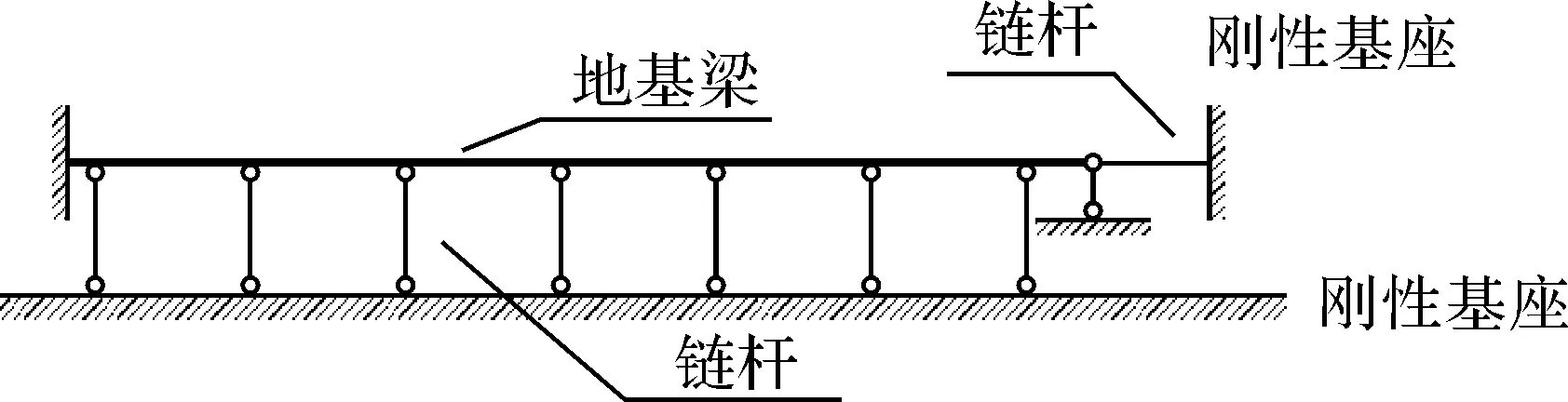
图5 考虑切向力梁的简化计算图

此时截面面积A=Lks/Es.

2 计算方法

设梁的弹性模量为E,惯性矩为I,截面面积为A,将结构离散后进行单元编号.为简化计算,将地基用一根链杆代替,如图6所示.

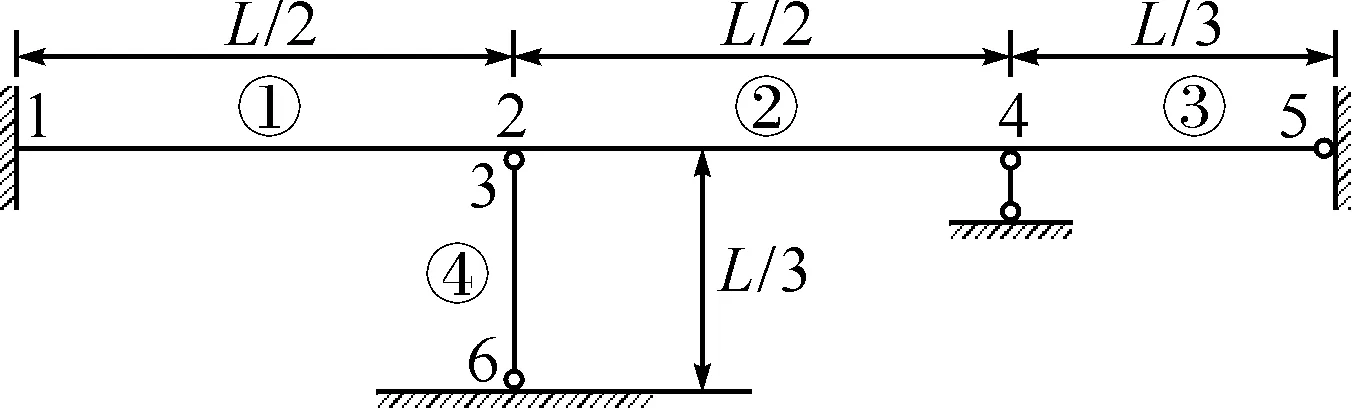
图6 简例计算图

根据(3)式和(4)式分别计算各单元刚度矩阵:

梁单元①:

梁单元②:

链杆单元③:

链杆单元④:

根据[K](1)～[K](4),采用先处理法形成总体刚度矩阵[K],在总体刚度矩阵中将所需求出的2、3、4结点的行和列形成6×6矩阵如下：

根据梁上外荷载作用,可求得梁上2、3、4结点的结点力和变形.即:

3 实 例

取梁长L=12 m,截面高H=1 m,宽B=0.5 m,在梁的3 m和6 m处作用有集中荷载，P=800 kN，梁的弹性模量E=2×107kN/m3,取土的侧限压缩模量Es=15 000 kN/m2,按照经典的Winkler地基模型,可求得梁最大弯矩和剪力为:

M=3 109.9 kN·m,N=392.9 kN.

而按照本文计算模型,可求得中截面弯矩和剪力为

M=2 931.7 kN·m，N=386.5 kN.

4 结 语

a. 本文构建了考虑切向摩阻力Winkler弹性地基梁内力的简化计算模型，在考虑了切向摩阻力的情况下对弹性地基梁进行设计计算，可避免因未考虑偏心受压而使设计偏于安全，对实际工程具有积极的意义.

b. 若取地基侧向系数ks=0，则相当于原Winkler地基模型.分析总体刚度矩阵可知，本文计算模型对梁弯矩和剪力的影响较小，而对梁的轴力有较大影响.

c. 本文计算模型无法反映梁在受压时边缘地基会出现的塑性变形和土体变形的连续性，但计算的结果能够满足工程精度的要求.

参考文献：

[1]周景星.基础工程[M].北京:清华大学出版社,1996.

[2]方姗丹,唐新军，杨京.考虑切向摩阻力的弹性地基梁求解[J].人民黄河,2010,32(2):130-133.

[3]赵更新.土木工程结构分析程序设计[M].北京:中国水利水电出版社,2001.

[4]谈至明.具有水平摩阻力的弹性地基上梁的解[J].力学与实践,1997,19(3):33-35.

[5]周继凯，杜钦庆.考虑水平作用力的改进文克勒地基模型[J].河海大学学报,2004,32(6):669-673.