两类多输出一阶拟Bent函数的构造

刘志高

(马鞍山职业技术学院,安徽 马鞍山 243031)

0 引 言

Bent函数是由Rothaus于1976年提出的一类特殊的非线性组合函数[1].它的非线性度达到最大,稳定性强,差分分布均匀.用于非线性组合器可以很好的抗击最佳仿射逼近攻击和差分分析攻击.但Bent函数也存在着一些缺陷.如:它不具有平衡性和相关免疫性,n元Bent函数的代数次数不超过n/2,限制n为偶数等.为了弥补Bent函数的这些不足,为弥补Bent函数的这些不足,胡磊等定义了半Bent函数[2],李世取教授等提出了k阶拟Bent函数的概念[3],它是包含Bent函数和半Bent函数的更大的函数类.它可以具有Bent函数所不具有的密码学性质,如:平衡性、扩散性、相关免疫性等.随后,人们对拟Bent函数作出了一系列的研究成果[4-9].这些研究表明,拟Bent函数是一类密码学性质良好的布尔函数,在密码设计及通信领域中有着广泛的应用.

分组密码的核心部件S-盒的设计中,常常采用具有多个良好密码学性质的多输出布尔函数.如何构造具有多种良好密码学性质的多输出布尔函数至为关键.人们在研究多输出函数时,总希望所选取的多输出函数的某些线性组合谱的绝对值尽可能均匀.仅就这一点而言,多输出Bent函数无疑就是最佳待选函数.但多输出Bent函数不可避免地带有Bent函数所固有的一些缺陷,如:非平衡性,相关免疫阶为零,其代数次数不超过变元数目n的一半,限制n为偶数等等.多输出拟Bent函数[10]可以弥补多输出Bent函数的这些不足,且具有多种良好的密码学性质,可广泛地应用于多输出前馈网,分组密码的S-盒设计等领域.

本文给出了两类多输出一阶拟Bent函数的构造方法,其中一类是平衡的,另一类是具有相关免疫性的.它们可广泛应用于分组密码的S-盒设计和最佳信号设计等领域.

1 基本定义

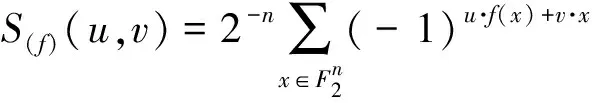
易知,对于固定的u,S(f)(u,v)就是布尔函数u·f(x)的一阶Walsh循环谱,即S(f)(u,v)=S(u·f)(v).

将此定义推广到多输出函数情形即得如下定义:

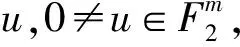
特别地,当k=0时,上述f(x)即为多输出Bent函数.当k=1时,上述f(x)即为多输出半Bent函数[12].

由定义3易得如下结论:

结论1n元m输出函数f(x)是多输出k阶拟Bent函数的必要条件是n与k奇偶性相同.

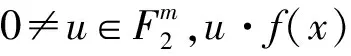
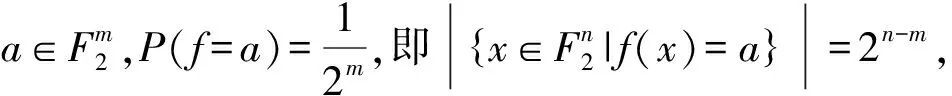
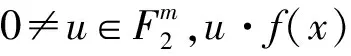
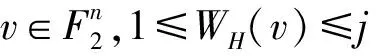
2 一类平衡多输出一阶拟Bent函数的构造

文献[2]给出了一类半Bent函数的构造方法,具体如下:

设n是奇数,n=2k-1,构造n元半Bent函数如下:

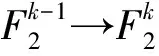
令f(X)=τ(X1)X2=τ1(X1)xk+τ2(X1)xk+1+…+τk(X1)x2k-1

(1)

引理3[2]由(1)式定义的f(X)是n元半Bent函数,并且

其中,W=(W1,W2),W1=(w1,…,wk-1),W2=(wk,wk+1,…,wn).

基于引理3,笔者于文献[12]中给出了一类多输出半Bent函数的构造方法,具体如下:

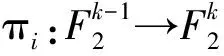
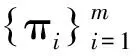
一般地,多输出一阶拟Bent函数不一定是平衡函数.下面将给出一类平衡多输出一阶拟Bent函数的构造方法.

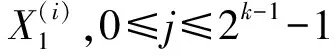
定理1 设f(X)是按引理4的方法所构造的多输出一阶拟Bent函数,则它为平衡函数的充要条件是对任意的1≤i1≤i2≤…≤ij≤m,矩阵Ei1⊕Ei2⊕…⊕Eij中均不存在全0的行向量.

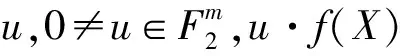
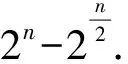
3 一类具有相关免疫性的多输出一阶拟Bent函数的构造

定理2 设f(X)是按引理4的方法所构造的多输出一阶拟Bent函数,则它具有m级l阶相关免疫性的充要条件是对任意的1≤i1≤i2≤…≤ij≤m,矩阵Ei1⊕Ei2⊕…⊕Eij的任意行向量中1的个数均大于l.

参考文献:

[1]Rothaus O S.On Bent Functions [J].Journal of Combinatorial Theory:Series A,1976,20:300-305.

[2]胡磊,裴定一,冯登国.一类bent函数的构造[J].中国科学院研究生院学报,2002,19(2):103-106.

[3]李世取,刘文芬,滕吉红.k阶拟Bent函数的性质及其应用[C]//谢仁宏.第7届全国青年通信学术会议论文集.北京:电子工业出版社,2001:939-943.

[4]ZHENG Y L,ZHANG X M.On plateau functions [J].IEEE Transactions on Information Theory,2001,47(3):1215-1223.

[5]滕吉红,李世取,刘文芬.k阶拟Bent函数在密码设计和通信中的应用[J].通信学报,2003,24(12):58-66.

[6]滕吉红,张文英,李世取,等.一类k阶拟Bent函数密码性质的矩阵特征[J].计算机学报,2004,27(4):543-547.

[7]张习勇,韩文报.拟Bent函数的性质和构造[J].数学学报,2004,47(6):1175-1184.

[8]何军,张建中.一类k阶拟Bent函数的构造[J].陕西师范大学学报:自然科学版,2005,33(3):18-20.

[9]胡斌金,晨辉,冯春海.Plateaued函数的密码学性质[J].电子与信息学报,2008,30(3):660-664.

[10]胡斌金,晨辉,史建红.多输出Plateaued函数的密码学性质[J].电子与信息学报,2009,31(6):1433-1437.

[11]冯登国.频谱理论及其在密码学中的应用[M].北京:科学出版社,2000:95-132.

[12]刘志高,张福泰,徐倩.一类多输出bent函数的构造[J].南京师范大学学报:工程技术版,2005,5(2):46-49.

[13]Pieprzyk J,Finkelstein G.Towards Effective Nonlinear Cryptosystem Design[C]//IEEE Proceedings,Part E: Computers and Digital Techniques.1998,135:325-335.

[14]刘志高,张福泰,徐倩.一类多输出半bent函数的构造及其密码学性质[J].南京师范大学学报:工程技术版,2006,6(1):38-42.